CBSE Class 10 Maths Notes Chapter 6 Triangles Pdf free download is part of Class 10 Maths Notes for Quick Revision. Here we have given NCERT Class 10 Maths Notes Chapter 6 Triangles. According to new CBSE Exam Pattern, MCQ Questions for Class 10 Maths Carries 20 Marks.
CBSE Class 10 Maths Notes Chapter 6 Triangles
SIMILAR FIGURES
- Two figures having the same shape but not necessary the same size are called similar figures.
- All congruent figures are similar but all similar figures are not congruent.
SIMILAR POLYGONS
Two polygons are said to be similar to each other, if:
(i) their corresponding angles are equal, and
(ii) the lengths of their corresponding sides are proportional
Example:
Any two line segments are similar since length are proportional
Any two circles are similar since radii are proportional
Any two squares are similar since corresponding angles are equal and lengths are proportional.
Note:
Similar figures are congruent if there is one to one correspondence between the figures.
∴ From above we deduce:
Any two triangles are similar, if their
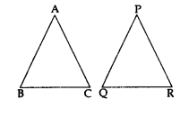
(i) Corresponding angles are equal
∠A = ∠P
∠B = ∠Q
∠C = ∠R
(ii) Corresponding sides are proportional
\(\frac { AB }{ PQ } =\frac { AC }{ PR } =\frac { BC }{ QR } \)
THALES THEOREM OR BASIC PROPORTIONALITY THEORY
Theorem 1:
State and prove Thales’ Theorem.
Statement:
If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
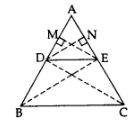
Given: In ∆ABC, DE || BC.
To prove: \(\frac { AD }{ DB } =\frac { AE }{ EC } \)
Const.: Draw EM ⊥ AD and DN ⊥ AE. Join B to E and C to D.
Proof: In ∆ADE and ∆BDE,
\(\frac { ar(\Delta ADE) }{ ar(\Delta BDE) } =\frac { \frac { 1 }{ 2 } \times AD\times EM }{ \frac { 1 }{ 2 } \times DB\times EM } =\frac { AD }{ DB } \) ……..(i) [Area of ∆ = \(\frac { 1 }{ 2 }\) x base x corresponding altitude
In ∆ADE and ∆CDE,
\(\frac { ar(\Delta ADE) }{ ar(\Delta CDE) } =\frac { \frac { 1 }{ 2 } \times AE\times DN }{ \frac { 1 }{ 2 } \times EC\times DN } =\frac { AE }{ EC } \)
∵ DE || BC …[Given
∴ ar(∆BDE) = ar(∆CDE)
…[∵ As on the same base and between the same parallel sides are equal in area
From (i), (ii) and (iii),
\(\frac { AD }{ DB } =\frac { AE }{ EC } \)
CRITERION FOR SIMILARITY OF TRIANGLES
Two triangles are similar if either of the following three criterion’s are satisfied:
- AAA similarity Criterion. If two triangles are equiangular, then they are similar.
- Corollary(AA similarity). If two angles of one triangle are respectively equal to two angles of another triangle, then the two triangles are similar.
- SSS Similarity Criterion. If the corresponding sides of two triangles are proportional, then they are similar.
- SAS Similarity Criterion. If in two triangles, one pair of corresponding sides are proportional and the included angles are equal, then the two triangles are similar.
Results in Similar Triangles based on Similarity Criterion:
- Ratio of corresponding sides = Ratio of corresponding perimeters
- Ratio of corresponding sides = Ratio of corresponding medians
- Ratio of corresponding sides = Ratio of corresponding altitudes
- Ratio of corresponding sides = Ratio of corresponding angle bisector segments.
AREA OF SIMILAR TRIANGLES
Theorem 2.
The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
Given: ∆ABC ~ ∆DEF
To prove: \(\frac { ar(\Delta ABC) }{ ar(\Delta DEF) } =\frac { { AB }^{ 2 } }{ { DE }^{ 2 } } =\frac { { BC }^{ 2 } }{ { EF }^{ 2 } } =\frac { { AC }^{ 2 } }{ { DF }^{ 2 } } \)
Const.: Draw AM ⊥ BC and DN ⊥ EF.
Proof: In ∆ABC and ∆DEF
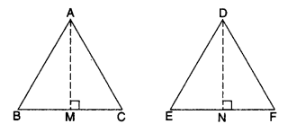
\(\frac { ar(\Delta ABC) }{ ar(\Delta DEF) } =\frac { \frac { 1 }{ 2 } \times BC\times AM }{ \frac { 1 }{ 2 } \times EF\times DN } =\frac { BC }{ EF } .\frac { AM }{ DN } \) …(i) ……[Area of ∆ = \(\frac { 1 }{ 2 }\) x base x corresponding altitude
∵ ∆ABC ~ ∆DEF
∴ \(\frac { AB }{ DE } =\frac { BC }{ EF } \) …..(ii) …[Sides are proportional
∠B = ∠E ……..[∵ ∆ABC ~ ∆DEF
∠M = ∠N …..[each 90°
∴ ∆ABM ~ ∆DEN …………[AA similarity
∴ \(\frac { AB }{ DE } =\frac { AM }{ DN } \) …..(iii) …[Sides are proportional
From (ii) and (iii), we have: \(\frac { BC }{ EF } =\frac { AM }{ DN } \) …(iv)
From (i) and (iv), we have: \(\frac { ar(\Delta ABC) }{ ar(\Delta DEF) } =\frac { BC }{ EF } .\frac { BC }{ EF } =\frac { { BC }^{ 2 } }{ { EF }^{ 2 } } \)
Similarly, we can prove that
\(\frac { ar(\Delta ABC) }{ ar(\Delta DEF) } =\frac { { AB }^{ 2 } }{ { DE }^{ 2 } } =\frac { AC^{ 2 } }{ DF^{ 2 } } \)
∴\(\frac { ar(\Delta ABC) }{ ar(\Delta DEF) } =\frac { { AB }^{ 2 } }{ { DE }^{ 2 } } =\frac { { BC }^{ 2 } }{ { EF }^{ 2 } } =\frac { AC^{ 2 } }{ DF^{ 2 } } \)
Results based on Area Theorem:
- Ratio of areas of two similar triangles = Ratio of squares of corresponding altitudes
- Ratio of areas of two similar triangles = Ratio of squares of corresponding medians
- Ratio of areas of two similar triangles = Ratio of squares of corresponding angle bisector segments.
Note:
If the areas of two similar triangles are equal, the triangles are congruent.
PYTHAGORAS THEOREM
Theorem 3:
State and prove Pythagoras’ Theorem.
Statement:
Prove that, in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Given: ∆ABC is a right triangle right-angled at B.
To prove: AB² + BC² = AC²
Const.: Draw BD ⊥ AC
Proof: In ∆s ABC and ADB,
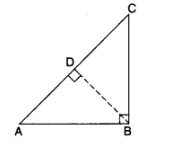
∠A = ∠A …[common
∠ABC = ∠ADB …[each 90°
∴ ∆ABC ~ ∆ADB …[AA Similarity
∴ \(\frac { AB }{ AD } =\frac { AC }{ AB } \) ………[sides are proportional]
⇒ AB² = AC.AD
Now in ∆ABC and ∆BDC
∠C = ∠C …..[common]
∠ABC = ∠BDC ….[each 90°]
∴ ∆ABC ~ ∆BDC …..[AA similarity]
∴ \(\frac { BC }{ DC } =\frac { AC }{ BC } \) ……..[sides are proportional]
BC² = AC.DC …(ii)
On adding (i) and (ii), we get
AB² + BC² = ACAD + AC.DC
⇒ AB² + BC² = AC.(AD + DC)
AB² + BC² = AC.AC
∴AB² + BC² = AC²
CONVERSE OF PYTHAGORAS THEOREM
Theorem 4:
State and prove the converse of Pythagoras’ Theorem.
Statement:
Prove that, in a triangle, if square of one side is equal to the sum of the squares of the other two sides, then the angle opposite the first side is a right angle.
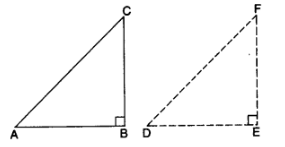
Given: In ∆ABC, AB² + BC² = AC²
To prove: ∠ABC = 90°
Const.: Draw a right angled ∆DEF in which DE = AB and EF = BC
Proof: In ∆ABC,
AB² + BC² = AC² …(i) [given]
In rt. ∆DEF
DE² + EF² = DF² …[by pythagoras theorem]
AB² + BC² = DF² …..(ii) …[DE = AB, EF = BC]
From (i) and (ii), we get
AC² = DF²
⇒ AC = DF
Now, DE = AB …[by cont]
EF = BC …[by cont]
DF = AC …….[proved above]
∴ ∆DEF ≅ ∆ABC ……[sss congruence]
∴ ∠DEF = ∠ABC …..[CPCT]
∠DEF = 90° …[by cont]
∴ ∠ABC = 90°
Results based on Pythagoras’ Theorem:
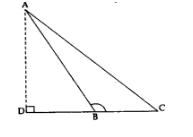
(i) Result on obtuse Triangles.
If ∆ABC is an obtuse angled triangle, obtuse angled at B,
If AD ⊥ CB, then
AC² = AB² + BC² + 2 BC.BD
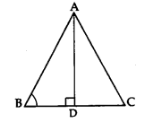
(ii) Result on Acute Triangles.
If ∆ABC is an acute angled triangle, acute angled at B, and AD ⊥ BC, then
AC² = AB² + BC² – 2 BD.BC.
Class 10 Maths Notes
- Chapter 1 Real Numbers Class 10 Notes
- Chapter 2 Polynomials Class 10 Notes
- Chapter 3 Pair of Linear equations in Two Variables Class 10 Notes
- Chapter 4 Quadratic Equations Class 10 Notes
- Chapter 5 Arithmetic Progressions Class 10 Notes
- Chapter 6 Triangles Class 10 Notes
- Chapter 7 Coordinate Geometry Class 10 Notes
- Chapter 8 Introduction to Trigonometry Class 10 Notes
- Chapter 9 Some Applications of Trigonometry Class 10 Notes
- Chapter 10 Circles Class 10 Notes
- Chapter 11 Constructions Class 10 Notes
- Chapter 12 Areas related to Circles Class 10 Notes
- Chapter 13 Surface Areas and Volumes Class 10 Notes
- Chapter 14 Statistics Class 10 Notes
- Chapter 15 Probability Class 10 Notes