CBSE Class 10 Maths Notes Chapter 12 Areas related to Circles Pdf free download is part of Class 10 Maths Notes for Quick Revision. Here we have given NCERT Class 10 Maths Notes Chapter 12 Areas related to Circles. According to new CBSE Exam Pattern, MCQ Questions for Class 10 Maths Carries 20 Marks.
CBSE Class 10 Maths Notes Chapter 12 Areas related to Circles
Circumference of a circle = 2πr
Area of a circle = πr2 …[where r is the radius of a circle]
Area of a semi-circle = \(\frac { { \pi r }^{ 2 } }{ 2 }\)
Area of a circular path or ring:
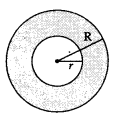
Let ‘R’ and ‘r’ he radii of two circles
Then area of shaded part = πR2 – πr2 = π(R2 – r2) = π(R + r)(R – r)
Minor arc and Major Arc: An arc length is called a major arc if the arc length enclosed by the two radii is greater than a semi-circle.
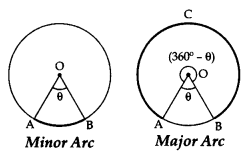
If the arc subtends angle ‘θ’ at the centre, then the
Length of minor arc = \(\frac { \theta }{ 360 } \times 2\pi r=\frac { \theta }{ 180 } \times \pi r\)
Length of major arc = \(\left( \frac { 360-\theta }{ 360 } \right) \times 2\pi r\)
Sector of a Circle and its Area
A region of a circle is enclosed by any two radii and the arc intercepted between two radii is called the sector of a circle.
(i) A sector is called a minor sector if the minor arc of the circle is part of its boundary.
\(\hat { OAB }\) is minor sector.
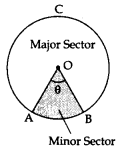
Area of minor sector = \(\frac { \theta }{ 360 } \left( { \pi r }^{ 2 } \right)\)
Perimeter of minor sector = \(2r+\frac { \theta }{ 360 } \left( { 2\pi r } \right) \)
(ii) A sector is called a major sector if the major arc of the circle is part of its boundary.
\(\hat { OACB }\) is major sector
Area of major sector = \(\left( \frac { 360-\theta }{ 360 } \right) \left( { \pi r }^{ 2 } \right)\)
Perimeter of major sector = \(2r+\left( \frac { 360-\theta }{ 360 } \right) \left( { 2\pi r } \right)\)
Minor Segment: The region enclosed by an arc and a chord is called a segment of the circle. The region enclosed by the chord PQ & minor arc PRQ is called the minor segment.
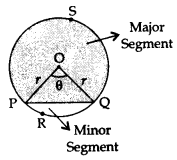
Area of Minor segment = Area of the corresponding sector – Area of the corresponding triangle
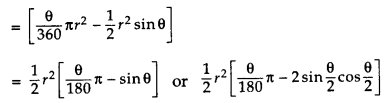
Major Segment: The region enclosed by the chord PQ & major arc PSQ is called the major segment.
Area of major segment = Area of a circle – Area of the minor segment
Area of major sector + Area of triangle
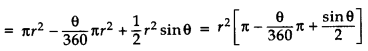

NCERT Notes for Class 10 Maths
- Chapter 1 Real Numbers Class 10 Notes
- Chapter 2 Polynomials Class 10 Notes
- Chapter 3 Pair of Linear equations in Two Variables Class 10 Notes
- Chapter 4 Quadratic Equations Class 10 Notes
- Chapter 5 Arithmetic Progressions Class 10 Notes
- Chapter 6 Triangles Class 10 Notes
- Chapter 7 Coordinate Geometry Class 10 Notes
- Chapter 8 Introduction to Trigonometry Class 10 Notes
- Chapter 9 Some Applications of Trigonometry Class 10 Notes
- Chapter 10 Circles Class 10 Notes
- Chapter 11 Constructions Class 10 Notes
- Chapter 12 Areas related to Circles Class 10 Notes
- Chapter 13 Surface Areas and Volumes Class 10 Notes
- Chapter 14 Statistics Class 10 Notes
- Chapter 15 Probability Class 10 Notes
We hope the given CBSE Class 10 Maths Notes Chapter 12 Areas related to Circles Pdf free download will help you. If you have any query regarding NCERT Class 10 Maths Notes Chapter 12 Areas related to Circles, drop a comment below and we will get back to you at the earliest.