CBSE Class 10 Maths Notes Chapter 10 Circles Pdf free download is part of Class 10 Maths Notes for Quick Revision. Here we have given NCERT Class 10 Maths Notes Chapter 10 Circles. According to new CBSE Exam Pattern, MCQ Questions for Class 10 Maths Carries 20 Marks.
CBSE Class 10 Maths Notes Chapter 10 Circles
Circle: A circle is a collection of all points in a plane which are at a constant distance from a fixed point.
Centre: The fixed point is called the centre.
Radius: The constant distance from the centre is called the radius.
Chord: A line segment joining any two points on a circle is called a chord.
Diameter: A chord passing through the centre of the circle is called diameter. It is the longest chord.
Tangent: When a line meets the circle at one point or two coincidings The line is known as points, a tangent.
The tangent to a circle is perpendicular to the radius through the point of contact.
⇒ OP ⊥ AB
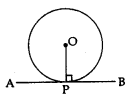
The lengths of the two tangents from an external point to a circle are equal.
⇒ AP = PB

Length of Tangent Segment
PB and PA are normally called the lengths of tangents from outside point P.
Properties of Tangent to Circle
Theorem 1: Prove that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
Given: XY is a tangent at point P to the circle with centre O.
To prove: OP ⊥ XY
Construction: Take a point Q on XY other than P and join OQ
Proof: If point Q lies inside the circle, then XY will become a secant and not a tangent to the circle
OQ > OP
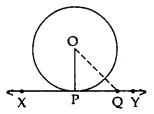
This happens with every point on line XY except point P. OP is the shortest of all the distances of point O the points of XY
OP ⊥ XY …[Shortest side is the perpendicular]
Theorem 2: A line drawn through the endpoint of a radius and perpendicular to it, is tangent to the circle.
Given: A circle C(O, r) and a line APB is perpendicular to OP, where OP is the radius.
To prove: AB is tangent at P.
Construction: Take a point Q on line AB, different from P, and join OQ.
Proof: Since OP ⊥ AB
OP < OQ ⇒ OQ > OP
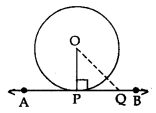
Point Q lies outside the circle.
Therefore, every point on AB, other than P, lies outside the circle.
This shows that AB meets the circle at point P.
Hence, AP is tangent to the circle at P.
Theorem 3: Prove that the lengths of tangents drawn from an external point to a circle are equal
Given: PT and PS are tangents from an external point P to the circle with centre O.
To prove: PT = PS
Construction: Join O to P, T and S.
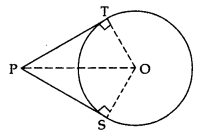
Proof: In ∆OTP and ∆OSP.
OT = OS …[radii of the same circle]
OP = OP …[common]
∠OTP = ∠OSP …[each 90°]
∆OTP = ∆OSP …[R.H.S.]
PT = PS …[c.p.c.t.]
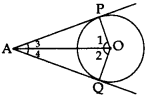
Note: If two tangents are drawn to a circle from an external point, then:
- They subtend equal angles at the centre i.e., ∠1 = ∠2.
- They are equally inclined to the segment joining the centre to that point i.e., ∠3 = ∠4.
∠OAP = ∠OAQ
Class 10 Maths Notes
- Chapter 1 Real Numbers Class 10 Notes
- Chapter 2 Polynomials Class 10 Notes
- Chapter 3 Pair of Linear equations in Two Variables Class 10 Notes
- Chapter 4 Quadratic Equations Class 10 Notes
- Chapter 5 Arithmetic Progressions Class 10 Notes
- Chapter 6 Triangles Class 10 Notes
- Chapter 7 Coordinate Geometry Class 10 Notes
- Chapter 8 Introduction to Trigonometry Class 10 Notes
- Chapter 9 Some Applications of Trigonometry Class 10 Notes
- Chapter 10 Circles Class 10 Notes
- Chapter 11 Constructions Class 10 Notes
- Chapter 12 Areas related to Circles Class 10 Notes
- Chapter 13 Surface Areas and Volumes Class 10 Notes
- Chapter 14 Statistics Class 10 Notes
- Chapter 15 Probability Class 10 Notes