CBSE Class 10 Maths Notes Chapter 13 Surface Areas and Volumes Pdf free download is part of Class 10 Maths Notes for Quick Revision. Here we have given NCERT Class 10 Maths Notes Chapter 13 Surface Areas and Volumes. According to new CBSE Exam Pattern, MCQ Questions for Class 10 Maths Carries 20 Marks.
CBSE Class 10 Maths Notes Chapter 13 Surface Areas and Volumes
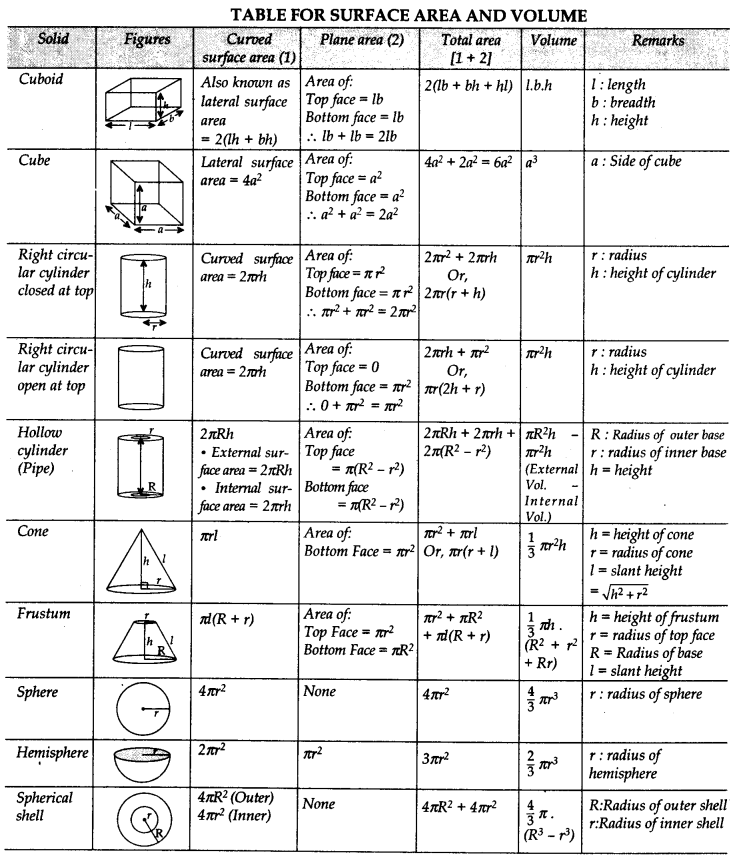
SURFACE AREA AND VOLUME OF COMBINATIONS
Cone on a Cylinder.
r = radius of cone & cylinder;
h1 = height of cone
h2 = height of cylinder
Total Surface area = Curved surface area of cone + Curved surface area of cylinder + area of circular base
= πrl + 2πrh2 +πr2;
Slant height, l = \(\sqrt { { r }^{ 2 }+{ { { h }_{ 1 }^{ 2 } } } }\)
Total Volume = Volume of cone + Volume of cylinder
= \(\frac { 1 }{ 3 } { \pi r }^{ 2 }{ h }_{ 1 }+{ \pi r }^{ 2 }{ h }_{ 2 }\)
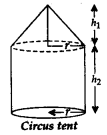
Cone on a Hemisphere:
h = height of cone;
l = slant height of cone = \(\sqrt { { r }^{ 2 }+{ h }^{ 2 } }\)
r = radius of cone and hemisphere
Total Surface area = Curved surface area of cone + Curved surface area of hemisphere = πrl + 2πr2
Volume = Volume of cone + Volume of hemisphere = \(\frac { 1 }{ 3 } { \pi r }^{ 2 }h+\frac { 2 }{ 3 } { \pi r }^{ 3 }\)
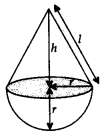
Conical Cavity in a Cylinder
r = radius of cone and cylinder;
h = height of cylinder and conical cavity;
l = Slant height
Total Surface area = Curved surface area of cylinder + Area of the bottom face of cylinder + Curved surface area of cone = 2πrh + πr2 + πrl
Volume = Volume of cylinder – Volume of cone = \({ \pi r }^{ 2 }h-\frac { 1 }{ 3 } { \pi r }^{ 2 }h=\frac { 2 }{ 3 } { \pi r }^{ 2 }h\)
Cones on Either Side of the Cylinder.
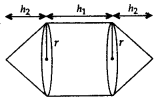
r = radius of cylinder and cone;
h1 = height of the cylinder
h2 = height of cones
Slant height of cone, l = \(\sqrt { { h }_{ 2 }^{ 2 }+{ r }^{ 2 } }\)
Surface area = Curved surface area of 2 cones + Curved surface area of cylinder = 2πrl + 2πrh1
Volume = 2(Volume of cone) + Volume of cylinder = \(\frac { 2 }{ 3 } { \pi r }^{ 2 }{ h }_{ 2 }+{ \pi r }^{ 2 }{ h }_{ 1 }\)
Cylinder with Hemispherical Ends.
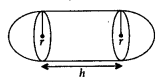
r = radius of cylinder and hemispherical ends;
h = height of cylinder
Total surface area= Curved surface area of cylinder + Curved surface area of 2 hemispheres = 2πrh + 4πr2
Volume = Volume of cylinder + Volume of 2 hemispheres = \({ \pi r }^{ 2 }h+\frac { 4 }{ 3 } { \pi r }^{ 3 }\)
Hemisphere on Cube or Hemispherical Cavity on Cube
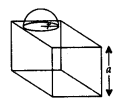
a = side of cube;
r = radius of hemisphere.
Surface area = Surface area of cube – Area of hemisphere face + Curved surface area of hemisphere
= 6a2 – πr2 + 2πr2 = 6a2 + πr2
Volume = Volume of cube + Volume of hemisphere = \({ a }^{ 3 }+\frac { 4 }{ 3 } { \pi r }^{ 3 }\)
Hemispherical Cavity in a Cylinder
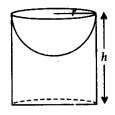
r = radius of hemisphere;
h = height of cylinder
Total surface area = Curved surface area of cylinder + Surface area of base + Curved surface area of hemisphere
= 2πrh + πr2 + 2πr2 = 2πrh + 3πr2
Volume = Volume of cylinder – Volume of hemisphere = \({ \pi r }^{ 2 }h-\frac { 2 }{ 3 } { \pi r }^{ 3 }\)
NCERT Notes for Class 10 Maths
- Chapter 1 Real Numbers Class 10 Notes
- Chapter 2 Polynomials Class 10 Notes
- Chapter 3 Pair of Linear equations in Two Variables Class 10 Notes
- Chapter 4 Quadratic Equations Class 10 Notes
- Chapter 5 Arithmetic Progressions Class 10 Notes
- Chapter 6 Triangles Class 10 Notes
- Chapter 7 Coordinate Geometry Class 10 Notes
- Chapter 8 Introduction to Trigonometry Class 10 Notes
- Chapter 9 Some Applications of Trigonometry Class 10 Notes
- Chapter 10 Circles Class 10 Notes
- Chapter 11 Constructions Class 10 Notes
- Chapter 12 Areas related to Circles Class 10 Notes
- Chapter 13 Surface Areas and Volumes Class 10 Notes
- Chapter 14 Statistics Class 10 Notes
- Chapter 15 Probability Class 10 Notes
We hope the given CBSE Class 10 Maths Notes Chapter 13 Surface Areas and Volumes Pdf free download will help you. If you have any query regarding NCERT Class 10 Maths Notes Chapter 13 Surface Areas and Volumes, drop a comment below and we will get back to you at the earliest.