CBSE Class 10 Maths Notes Chapter 9 Some Applications of Trigonometry Pdf free download is part of Class 10 Maths Notes for Quick Revision. Here we have given NCERT Class 10 Maths Notes Chapter 9 Some Applications of Trigonometry. According to new CBSE Exam Pattern, MCQ Questions for Class 10 Maths Carries 20 Marks.
CBSE Class 10 Maths Notes Chapter 9 Some Applications of Trigonometry
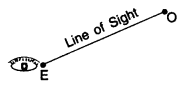
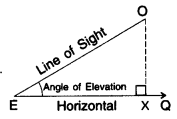
Line of Sight
When an observer looks from a point E (eye) at object O then the straight line EO between eye E and object O is called the line of sight.
Horizontal
When an observer looks from a point E (eye) to another point Q which is horizontal to E, then the straight line, EQ between E and Q is called the horizontal line.
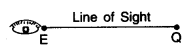
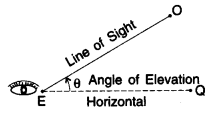
Angle of Elevation
When the eye is below the object, then the observer has to look up from point E to object O. The measure of this rotation (angle θ) from the horizontal line is called the angle of elevation.
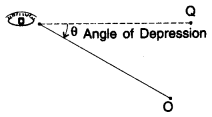
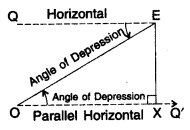
Angle of Depression
When the eye is above the object, then the observer has to look down from point E to the object. The horizontal line is now parallel to the ground. The measure of this rotation (angle θ) from the horizontal line is called the angle of depression.
How to convert the above figure into the right triangle.
Case I: Angle of Elevation is known
Draw OX perpendicular to EQ.
Now ∠OXE = 90°
ΔOXE is a rt. Δ, where
OE = hypotenuse
OX = opposite side (Perpendicular)
EX = adjacent side (Base)
Case II: Angle of Depression is known
(i) Draw OQ’parallel to EQ
(ii) Draw perpendicular EX on OQ’.
(iii) Now ∠QEO = ∠EOX = Interior alternate angles
ΔEXO is an rt. Δ. where
EO = hypotenuse
OX = adjacent side (base)
EX = opposite side (Perpendicular)
- Choose a trigonometric ratio in such a way that it considers the known side and the side that you wish to calculate.
- The eye is always considered at ground level unless the problem specifically gives the height of the observer.
The object is always considered a point.
Some People Have
Sin θ = \(\frac { Perpendicular }{ Hypotenuse }\)
Curly Black Hair
Cos θ = \(\frac { Base }{ Hypotenuse }\)
Turning Permanent Black.
Tan θ = \(\frac { Perpendicular }{ Base }\)
Class 10 Maths Notes
- Chapter 1 Real Numbers Class 10 Notes
- Chapter 2 Polynomials Class 10 Notes
- Chapter 3 Pair of Linear equations in Two Variables Class 10 Notes
- Chapter 4 Quadratic Equations Class 10 Notes
- Chapter 5 Arithmetic Progressions Class 10 Notes
- Chapter 6 Triangles Class 10 Notes
- Chapter 7 Coordinate Geometry Class 10 Notes
- Chapter 8 Introduction to Trigonometry Class 10 Notes
- Chapter 9 Some Applications of Trigonometry Class 10 Notes
- Chapter 10 Circles Class 10 Notes
- Chapter 11 Constructions Class 10 Notes
- Chapter 12 Areas related to Circles Class 10 Notes
- Chapter 13 Surface Areas and Volumes Class 10 Notes
- Chapter 14 Statistics Class 10 Notes
- Chapter 15 Probability Class 10 Notes