NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers Ex 1.2

Ex 1.2 Class 10 Maths

Get Free NCERT Solutions for Class 10 Maths Chapter 1 Ex 1.2 PDF. Real Numbers Class 10 Maths NCERT Solutions are extremely helpful while doing homework. Exercise 1.2 Class 10 Maths NCERT Solutions were prepared by Experienced LearnCBSE.in Teachers. Detailed answers of all the questions in Chapter 1 maths class 10 Real Numbers Exercise 1.2 provided in NCERT TextBook.

Topics and Sub Topics in Class 10 Maths Chapter 1 Real Numbers:

Section Name	Topic Name
1	Real Numbers
1.1	Introduction
1.2	Euclid’s Division Lemma
1.3	The Fundamental Theorem of Arithmetic
1.4	Revisiting Irrational Numbers
1.5	Revisiting Rational Numbers and Their Decimal Expansions
1.6	Summary

• Class 10 Maths Real Numbers Ex 1.1
• प्रश्नावली 1.1 का हल हिंदी में वास्तविक संख्याएँ
• Class 10 Maths Real Numbers Ex 1.2
• प्रश्नावली 1.2 का हल हिंदी में वास्तविक संख्याएँ
• Class 10 Maths Real Numbers Ex 1.3
• प्रश्नावली 1.3 का हल हिंदी में वास्तविक संख्याएँ
• Class 10 Maths Real Numbers Ex 1.4
• प्रश्नावली 1.4  का हल हिंदी में वास्तविक संख्याएँ
• Real Numbers Class 10 Extra Questions

You can also download the free PDF of  Ex 1.2 Class 10 Real Numbers NCERT Solutions or save the solution images and take the print out to keep it handy for your exam preparation.

Board	CBSE
Textbook	NCERT
Class	Class 10
Subject	Maths
Chapter	Chapter 1
Chapter Name	Real Numbers
Exercise	Ex 1.2
Number of Questions Solved	7
Category	NCERT Solutions

Maths NCERT Solutions For Class 10 Chapter 1 Ex 1.2

NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers Ex 1.2 are part of NCERT Solutions for Class 10 Maths. Here we have given Maths NCERT Solutions Class 10 Chapter 1 Real Numbers Exercise 1.2

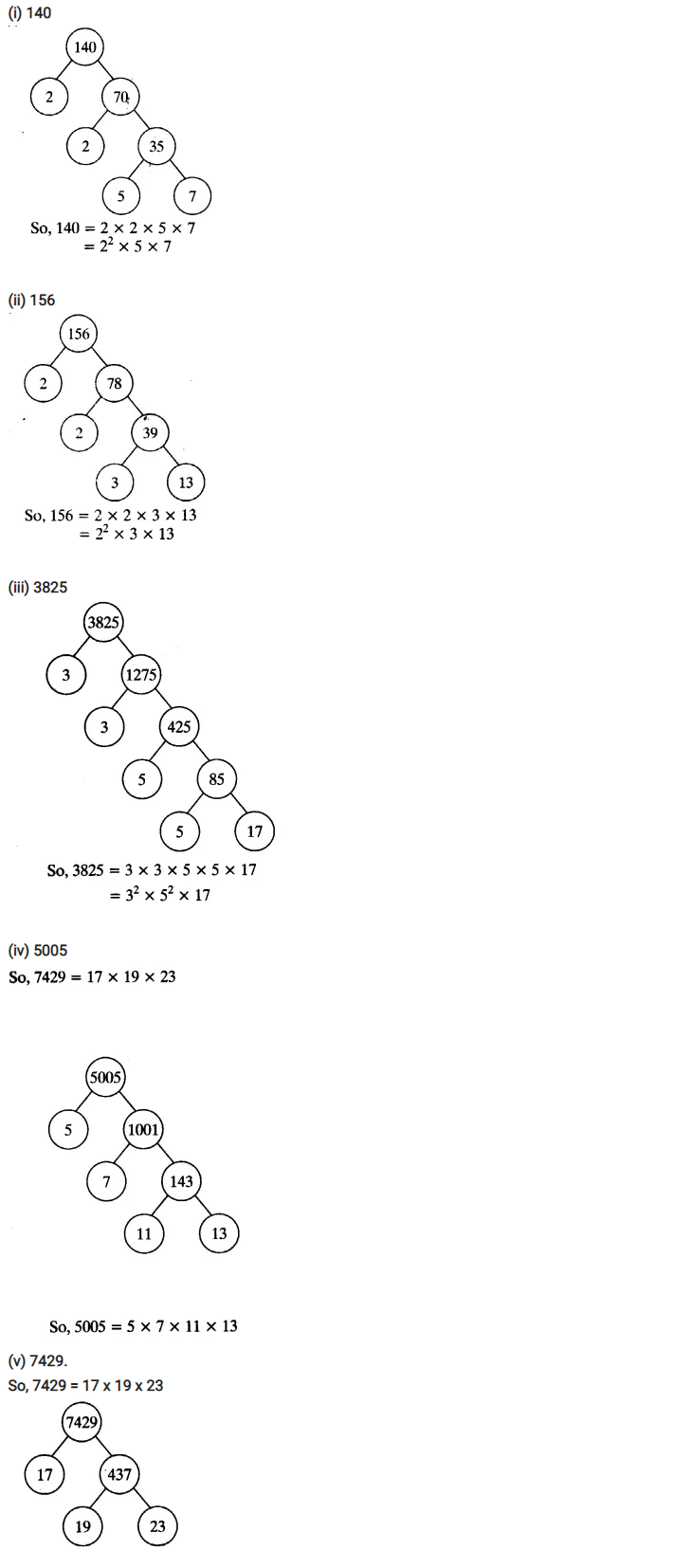
Ex 1.2 Class 10 Maths Question 1.
Express each number as a product of its prime factors:
(i) 140
(ii) 156
(iii) 3825
(iv) 5005
(v) 7429
Solution:

Ex 1.2 Class 10 Maths Question 2.
Find the LCM and HCF of the following pairs of integers and verify that LCM x HCF = Product of the two numbers:
(i) 26 and 91
(ii) 510 and 92
(iii) 336 and 54
Solution:

Ex 1.2 Class 10 Maths Question 3.
Find the LCM and HCF of the following integers by applying the prime factorization method:
(i) 12, 15 and 21
(ii) 17, 23 and 29
(iii) 8, 9 and 25
Solution:

Ex 1.2 Class 10 Maths Question 4:
Given that HCF (306, 657) = 9, find LCM (306, 657).

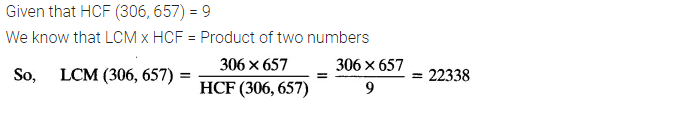
Ex 1.2 Class 10 Maths Question 5.
Check whether 6ⁿ can end with the digit 0 for any natural number n.

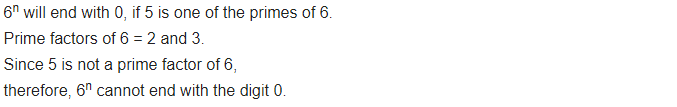
Ex 1.2 Class 10 Maths Question 6.
Explain why 7 x 11 x 13 + 13 and 7 x 6 x 5 x 4 x 3 x 2 x 1 + 5 are composite numbers.

Ex 1.2 Class 10 Maths Question 7.
There is a circular path around a sports field. Sonia takes 18 minutes to drive one round of the field, while Ravi takes 12 minutes for the same. Suppose they both start at the same point and at the same time and go in the same direction. After how many minutes will they meet again at the starting point?
Solution:

NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers (Hindi Medium) Ex 1.2