NCERT Solutions For Class 10 Maths Chapter 4 Quadratic Equations Ex 4.1

NCERT Solutions Class 10 Maths Chapter 4 Quadratic Equations – Here are all the Class 10 Maths Chapter 4 Quadratic Equations NCERT Solutions. This solution contains questions, answers, images, step by step explanation of the complete Chapter 4 titled Quadratic Equations in Class 10. If you are a student of Class 10 who is using NCERT Textbook to study Maths, then you must come across Chapter 4 Quadratic Equations. After you have studied lesson, you must be looking for answers to its textbook questions. Here you can get complete NCERT Solutions for Class 10 Maths Chapter 4 Quadratic Equations in one place.

• Class 10 Maths Quadratic Equations Ex 4.1
• प्रश्नावली 4.1 का हल हिंदी में
• Class 10 Maths Quadratic Equations Ex 4.2
• प्रश्नावली 4.2 का हल हिंदी में
• Class 10 Maths Quadratic Equations Ex 4.3
• प्रश्नावली 4.3 का हल हिंदी में
• Class 10 Maths Quadratic Equations Ex 4.4
• प्रश्नावली 4.4 का हल हिंदी में
• Quadratic Equations Class 10 Extra Questions

NCERT Solutions For Class 10 Maths Chapter 4 Quadratic Equations Ex 4.1

NCERT Solutions for Class 10 Maths Chapter 4 Quadratic Equations Ex 4.1 are part of NCERT Solutions for Class 10 Maths. Here we have given NCERT Solutions for Class 10 Maths Chapter 4 Quadratic Equations Ex 4.1.

Board	CBSE
Textbook	NCERT
Class	Class 10
Subject	Maths
Chapter	Chapter 4
Chapter Name	Quadratic Equations
Exercise	Ex 4.1
Number of Questions Solved	2
Category	NCERT Solutions

Ex 4.1 Class 10 Maths Question 1.
Check whether the following are quadratic equations:
(i) (x+ 1)²=2(x-3)
(ii) x – 2x = (- 2) (3-x)
(iii) (x – 2) (x + 1) = (x – 1) (x + 3)
(iv) (x – 3) (2x + 1) = x (x + 5)
(v) (2x – 1) (x – 3) = (x + 5) (x – 1)
(vi) x² + 3x + 1 = (x – 2)²
(vii) (x + 2)³ = 2x(x² – 1)
(viii) x³ -4x² -x + 1 = (x-2)³
Solution:

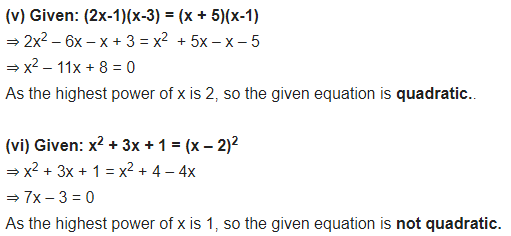
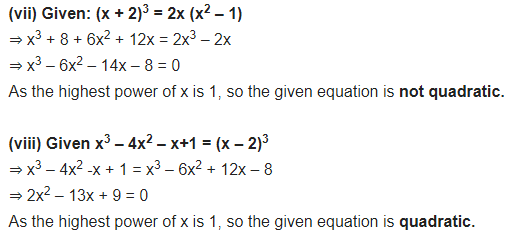
NCERT Solutions Class 10 Maths chapter 4 Quadratic Equations- Video

You can also watch the video solutions of NCERT Class10 Maths chapter 4 Quadratic Equations here.

Ex 4.1 Class 10 Maths Question 2.
Represent the following situations in the form of quadratic equations:
(i) The area of a rectangular plot is 528 m². The length of the plot (in metres) is one more than twice its breadth. We need to find the length and breadth of the plot.
(ii) The product of two consecutive positive integers is 306. We need to find the integers.
(iii) Rohan’s mother is 26 years older than him. The product of their ages (in years) 3 years from now will be 360. We would like to find Rohan’s present age.
(iv) A train travels a distance of 480 km at a uniform speed. If the speed had been 8 km/h less, then it would have taken 3 hours more to cover the same distance. We need to find the speed of the train.
Solution:

NCVT Mis Result 2019

NCERT Solutions Class 10 Maths chapter 4 Quadratic Equations

Class 10, Maths chapter 4, Quadratic Equations solutions are given below in PDF format. You can view them online or download PDF file for future use.

or save the solution images and take the print out to keep it handy for your exam preparation. Click Here to Download NCERT Solutions for Class 10 Maths chapter 4 Quadratic Equations.

NCERT Solutions for Class 10 Maths Chapter 4 Quadratic Equations (Hindi Medium) Ex 4.1

Class 10 Maths Quadratic Equations Mind Map

Quadratic Equation

Standard form of the quadratic equation in the variable x is an equation of the form ax2 + bx + c = 0, where a, b, c are real numbers and a ≠ 0.
Any equation of the form P(x) = 0, Where P(x) is a polynomial of degree 2, is a quadratic equation.

Zero(es)/Root(s) of Quadratic Equation

A real number α is said to be a root of the quadratic equation ax² + bx + c = 0, a ≠ 0 if aα² + bα + c = 0.
We can say that x = α, is a solution of the quadratic equation or that α satisfies the quadratic equation.
The zeroes of the quadratic polynomial ax² + bx + c = 0 and the roots of the equation ax² + bx + c = 0 are same. A quadratic equation has atmost two roots/zeroes.

Relation Between Zeroes and Co-efficient of a Quadratic Equation

If α and β are zeroes of the quadratic equation ax² + bx + c = 0, where a, b, c are real numbers and a ≠ 0 then

Methods of Solving Quadratic Equation

Following are the methods which are used to solve quadratic equations:

(i) Factorisation
(ii) Completing the square
(iii) Quadratic Formula

Methods of Factorisation

In this method we find the roots of a quadratic equation (ax² + bx + c = 0) by factorising LHS it into two linear factors and equating each factor to zero, e.g.,
6x² – x – 2 = 0
⇒ 6x² + 3x – 4x – 2 = 0 …(i)
⇒ 3x (2x + 1) – 2(2x + 1) = 0
⇒ (3x — 2) (2x + 1) = 0
⇒ 3x – 2 = 0 or 2x + 1 = 0

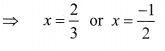
Necessary Condition : Product of 1st and last terms of eq. (i) should be equal to product of 2nd and 3rd terms of the same equation.

Method of Completing the Square

This is the method of converting L.H.S. of a quadratic equation which is not a perfect square into the sum or difference of a perfect square and a constant by adding and subtracting the suitable constant terms. E.g,
(1) x² + 4x – 5 = 0
⇒ x² + 2(2)(x) -5 = 0
⇒ x² + 2(2)(x) + (2)² – (2)² – 5 = 0
⇒ (x + 2)² – 4 – 5 = 0
⇒ (x + 2)² – 9 = 0
⇒ x + 2 = ± 3
⇒ x = —5, 1
(2) 3x² – 5x + 2 = 0

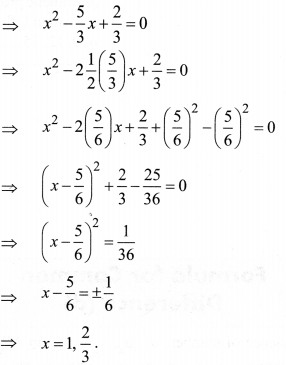
Quadratic Formula

Consider a quadratic equation: ax² + bx + c = 0.
If b² – 4ac ≥ 0, then the roots of the above equation are given by:

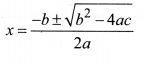
Nature of Roots

For quadratic equation ax² + bx + c = 0
(a ≠ 0), value of (b² – 4ac) is called discriminant of the equation and denoted as D.
D = b² – 4ac
Discriminant is very important in finding nature of the roots.
(i) If D = 0, then roots are real and equal.
(ii) If D > 0, then roots are real and unequal
(iii) If D < 0, then roots are not real.

We hope the NCERT Solutions for Class 10 Maths Chapter 4 Quadratic Equations Ex 4.1, help you. If you have any query regarding NCERT Solutions for Class 10 Maths Chapter 4 Quadratic Equations Exercise 4.1, drop a comment below and we will get back to you at the earliest.