NCERT Solutions for Class 10 Maths Chapter 6 Triangles Ex 6.5

Get Free NCERT Solutions for Class 10 Maths Chapter 6 Ex 6.5 PDF. Triangles Class 10 Maths NCERT Solutions are extremely helpful while doing your homework. Exercise 6.5 Class 10 Maths NCERT Solutions were prepared by Experienced LearnCBSE.in Teachers. Detailed answers of all the questions in Chapter 6 Maths Class 10 Triangles Exercise 6.5 provided in NCERT TextBook.

You can also download Maths NCERT Solutions Class 10 to help you to revise complete syllabus and score more marks in your examinations.

Free download NCERT Solutions for Class 10 Maths Chapter 6 Exercise 6.5 Triangles PDF in Hindi Medium as well as in English Medium for CBSE, Uttarakhand, Bihar, MP Board, Gujarat Board, AP SSC, TS SSC and UP Board students, who are using NCERT Books based on updated CBSE Syllabus for the session 2019-20.

• Triangles Class 10 Mind Map
• Triangles Class 10 Ex 6.1
• Triangles Class 10 Ex 6.1 in Hindi Medium
• Triangles Class 10 Ex 6.2
• Triangles Class 10 Ex 6.2 in Hindi Medium
• Triangles Class 10 Ex 6.3
• Triangles Class 10 Ex 6.3 in Hindi Medium
• Triangles Class 10 Ex 6.4
• Triangles Class 10 Ex 6.4 in Hindi Medium
• Triangles Class 10 Ex 6.5
• Triangles Class 10 Ex 6.5 in Hindi Medium
• Triangles Class 10 Ex 6.6
• Triangles Class 10 Ex 6.6 in Hindi Medium
• Extra Questions for Class 10 Maths Triangles
• Triangles Class 10 Notes Maths Chapter 6
• NCERT Exemplar Class 10 Maths Chapter 6 Triangles
• Important Questions for Class 10 Maths Chapter 6 Triangles

You can also download the free PDF of Ex 6.5 Class 10 Triangles NCERT Solutions or save the solution images and take the print out to keep it handy for your exam preparation.

Board	CBSE
Textbook	NCERT
Class	Class 10
Subject	Maths
Chapter	Chapter 6
Chapter Name	Triangles
Exercise	Ex 6.5
Number of Questions Solved	17
Category	NCERT Solutions

NCERT Solutions for Class 10 Maths Chapter 6 Triangles Ex 6.5

NCERT Solutions for Class 10 Maths Chapter 6 Triangles Ex Ex 6.5 are part of NCERT Solutions for Class 10 Maths. Here we have given NCERT Solutions for Class 10 Maths Chapter 6 Triangles Exercise 6.5

Question 1.
Sides of triangles are given below. Determine which of them are right triangles. In case of a right triangle, write the length of its hypotenuse.
(i) 7 cm, 24 cm, 25 cm
(ii) 3 cm, 8 cm, 6 cm
(iii) 50 cm, 80 cm, 100 cm
(iv) 13 cm, 12 cm, 5 cm
Solution:

Question 2.
PQR is a triangle right angled at P and M is a point on QR such that PM ⊥ QR. Show that PM² = QM X MR.
Solution:

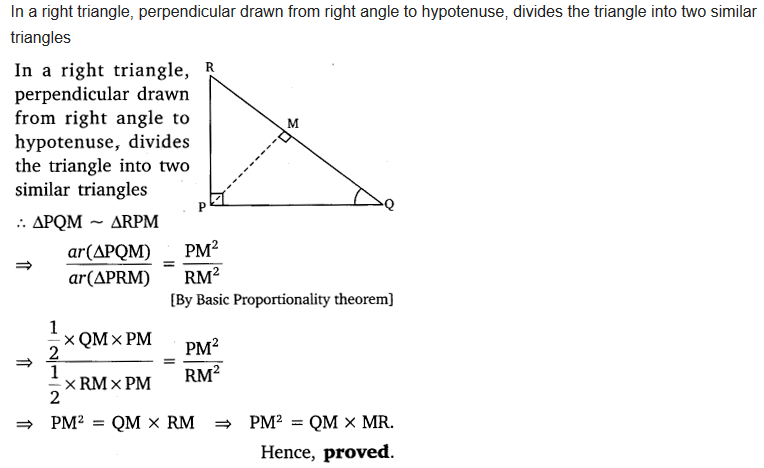
Download NCERT Solutions For Class 10 Maths Chapter 6 Triangles PDF

Question 3.
In the given figure, ABD is a triangle right angled at A and AC i. BD. Show that
(i) AB² = BC.BD
(ii) AC² = BC.DC
(iii) AD² = BD.CD
Solution:

Question 4.
ABC is an isosceles triangle right angled at C. Prove that AB² = 2AC².
Solution:

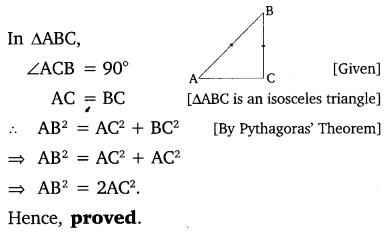
Question 5.
ABC is an isosceles triangle with AC = BC. If AB² = 2AC² , Prove that ABC is a right triangle.
Solution:

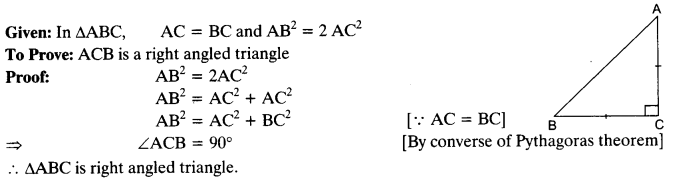
Question 6.
ABC is an equilateral triangle of side la. Find each of its altitudes.
Solution:

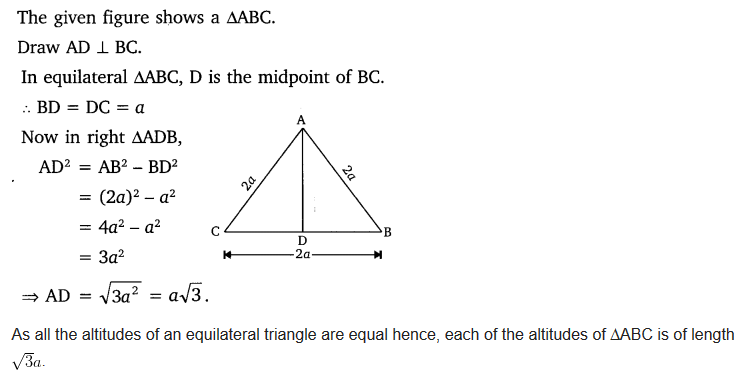
Question 7.
Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals.
Solution:

Question 8.
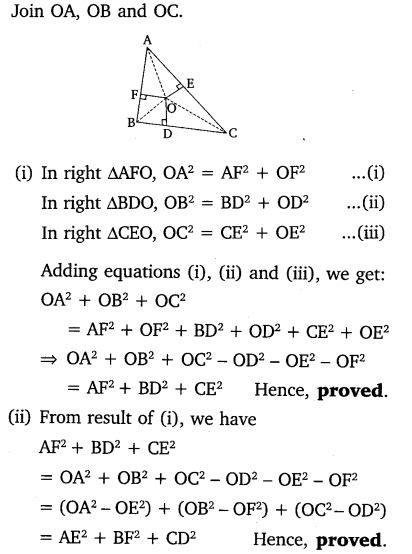
In the given figure, O is a point in the interior of a triangle ABC, OD ⊥ BC, OE ⊥ AC and OF ⊥ AB. Show that
(i) OA² + OB² + OC² – OD² – OE² – OF² = AF² + BD² + CE²
(ii) AF² + BD² + CE² = AE² + CD² + BF².
Solution:

Question 9.
A ladder 10 m long reaches a window 8 m above the ground. ind the distance of the foot of the ladder from base of the wall.
Solution:

Question 10.
A guy wire attached to a vertical pole of height 18 m is 24 m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?
Solution:

Question 11.
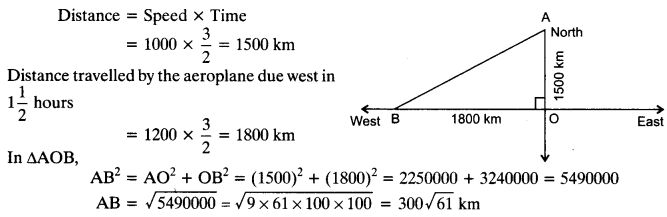
An aeroplane leaves an airport and flies due north at a speed of 1000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km per hour. How far apart will be the two planes after 1\(\frac { 1 }{ 2 }\) hours?
Solution:

Question 12.
Two poles of heights 6 m and 11m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops.
Solution:

Question 13.
D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that AE² + BD² = AB² + DE².
Solution:

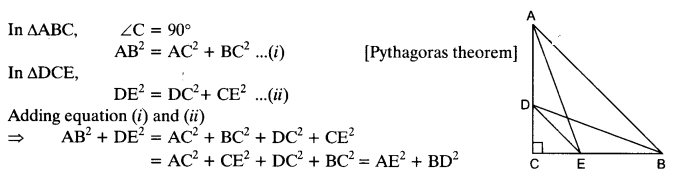
Question 14.
The perpendicular from A on side BC of a ∆ABC intersects BC at D such that DB = 3CD (see the figure). Prove that 2AB² = 2AC² + BC².
Solution:

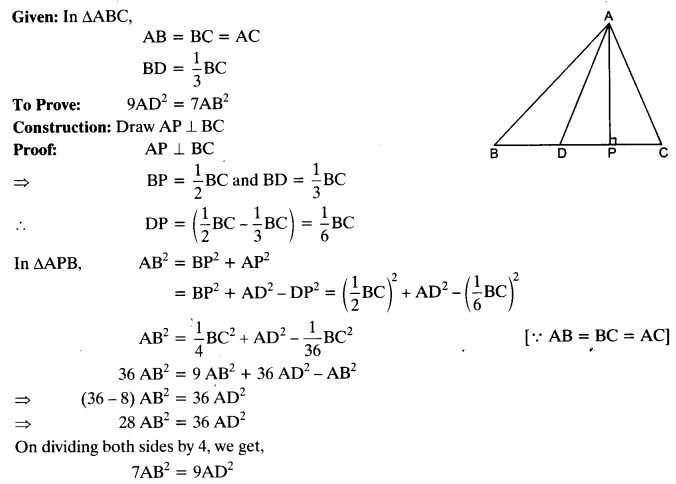
Question 15.
In an equilateral triangle ABC, D is a point on side BC, such that BD = \(\frac { 1 }{ 3 }\)BC. Prove that 9AD² = 7AB².
Solution:

Question 16.
In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.
Solution:

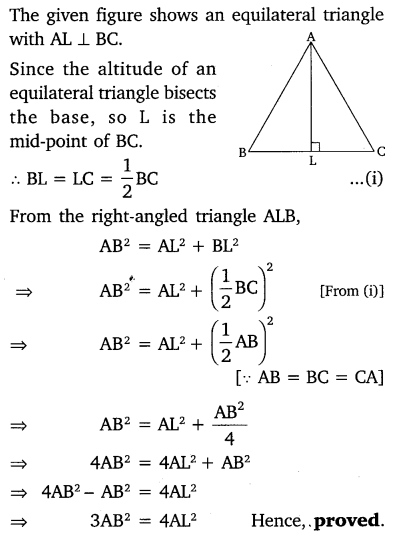
Question 17.
Tick the correct answer and justify : In ∆ABC, AB = 6\(\sqrt { 3 } \)cm, AC = 12 cm and BC = 6 cm. The angle B is:
(a) 120°
(b) 60°
(c) 90°
(d) 45
Solution:

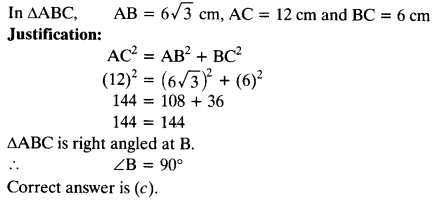
NCERT Solutions for Class 10 Maths NCERT Solutions Chapter 6 Ex 6.5 in Hindi Medium

एनसीईआरटी समाधान कक्षा 10 गणित त्रिभुज प्रश्नावली 6.5 (NCERT Page 164)

प्र० 1. कुछ त्रिभुजों की भुजाएँ नीचे दी गई हैं। निर्धरित कीजिए कि इनमें से कौन-कौन से त्रिभुज समकोण त्रिभुज हैं। इस स्थिति में कर्ण की लंबाई भी लिखिए।
(i) 7 cm, 24 cm, 25 cm
(ii) 3 cm, 8 cm, 6 cm
(iii) 50 cm, 80 cm, 100 cm
(iv) 13 cm, 12 cm, 5 cm

प्र० 2. PQR एक समकोण त्रिभुज है जिसका कोण P समकोण है तथा QR पर बिंदु M इस प्रकार स्थित है कि PM ⊥ QR है | दर्शाइए कि PM² = QM . MR है|

प्र० 3. आकृति 6.53 में ABD एक समकोण त्रिभुज है| जिसका कोण A समकोण है तथा AC ⊥ BD है| दर्शाइए कि
(i) AB² = BC . BD
(ii) AC² = BC . DC
(iii) AD² = BD . CD

प्र० 4. ABC एक समद्विबाहु त्रिभुज है जिसका कोण C समकोण है| सिद्ध कीजिए कि AB² = 2AC² है|

प्र० 5. ABC एक समद्विबाहु त्रिभुज है जिसमें AC = BC है| यदि AB² = 2AC² है, तो सिद्ध कीजिए कि ABC एक समकोण त्रिभुज है|

प्र० 6. एक समबाहु त्रिभुज ABC की भुजा 2a है। उसके प्रत्येक शीर्षलंब की लंबाई ज्ञात कीजिए।

प्र० 7. सिद्ध कीजिए कि एक समचतुर्भुज की भुजाओं के वर्गों का योग उसके विकर्णों के वर्गों के योग के बराबर होता है।

प्र० 9. 10 मी. लंबी एक सीढ़ी एक दीवार पर टिकाने पर भूमि से 8 मी. की ऊँचाई पर स्थित एक खिड़की तक पहुंचती है। दीवार के आधार से सीढ़ी के निचले सिरे की दूरी ज्ञात कीजिए।

प्र० 10. 18 मी. ऊंचे एक ऊर्ध्वाधर खंभे के ऊपरी सिरे से एक तार का एक सिरा जुड़ा हुआ है तथा तार का दूसरा सिरा एक बूंटे से जुड़ा हुआ है। खंभे के आधार से बँटे को कितनी दूरी पर गाड़ा जाए कि तार तना रहे जबकि तार की लंबाई 24 मी. है।
हलः माना AB एक तार तथा BC एक खंभा है।
माना बिन्दु A एक बँटे को प्रकट करता है।
AB = 24 मी. और BC = 18 मी.
अब, समकोण ΔABC में पाईथागोरस प्रमेय द्वारा।

प्र० 11. एक हवाई जहाज एक हवाई अड्डे से उत्तर की ओर 1000 कि.मी./घं. की चाल से उड़ता है। इसी समय एक अन्य हवाई जहाज उसी हवाई अड्डे से पश्चिम की ओर 1200 कि.मी./घं. की चाल से उड़ता है। 1\(\frac { 1 }{ 2 }\) घंटे के बाद दोनों हवाई जहाजों के बीच की दूरी कितनी होगी?

प्र० 12. दो खंभे जिनकी ऊँचाइयाँ 6 मी. और 11 मी. हैं तथा ये समतल भूमि पर खड़े हैं। यदि इनके तलों के बीच की दूरी 12 मी. है तो इनके ऊपरी सिरों के बीच की दूरी ज्ञात कीजिए।
हलः माना दो खंभे AB और CD है।
खंभों के तलों के बीच की दूरी AC = 12 मी.

प्र० 13. किसी त्रिभुज ABC जिसका कोण C समकोण है, की भुजाओं CA और CB पर क्रमश: बिंदु D औए E स्थित है| सिद्ध कीजिए कि AE² + BD² = AB² + DE² है|

प्र० 14. किसी त्रिभुज ABC के शीर्ष A से BC पर डाला गया लंब BC को बिंदु D पर इस प्रकार प्रतिच्छेद करता है कि DB = 3CD है| सिद्ध कीजिए कि : 2AB² = 2AC² + BC² है|

प्र० 15. किसी समबाहु त्रिभुज ABC की भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि BD = \(\frac { 1 }{ 3 }\) BC है। सिद्ध कीजिए कि 9AD² = 7AB² हैं।

प्र० 16. किसी समबाहु त्रिभुज में, सिद्ध कीजिए कि उसकी एक भुजा के वर्ग का तिगुना उसके एक शीर्षलंब के वर्ग के चार गुने के बराबर होता है|
हलः हमें प्राप्त है कि समबाहु ΔABC में, AD ⊥ BC
हम जानते हैं कि समबाहु A में शीर्षलम्ब संगत भुजा को समद्विभाजित करता है।
D, भुजा BC का मध्यबिन्दु है।
BD = DC [प्रत्येक = \(\frac { 1 }{ 2 }\) BC]

प्र० 17. सही उत्तर चुनकर उनका औचित्य दीजिए:
ΔABC में, AB = 63 सेमी., AC = 12 सेमी. अ
BC = 6 सेमी. है। कोण B हैः
(A) 120°
(B) 60°
(C) 90°
(D) 45°
हलः हमें प्राप्त है:
AB = 6√3 सेमी.
AC = 12 सेमी.
BC = 6 सेमी.
AB² = (6√3)² = 36 x 3 = 108
AC² = 12² = 144
BC² = 6² = 36
चूंकि, 144 = 108 + 36
अर्थात् AC² = AB² + BC²
ΔABC एक समकोण त्रिभुज है जिसमें
∠B = 90° है।
अतः उत्तर (C) अर्थात् 90° सही है।

We hope the NCERT Solutions for Class 10 Maths Chapter 6 Triangles Ex 6.5, help you. If you have any query regarding NCERT Solutions for Class 10 Maths Chapter 6 Triangles Exercise 6.5, drop a comment below and we will get back to you at the earliest.