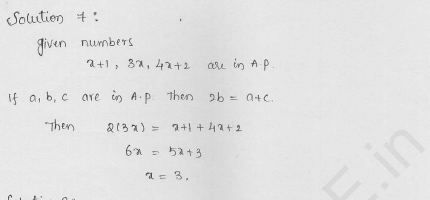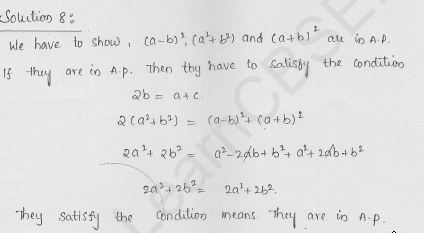RD Sharma Class 10 Solutions Chapter 9 Arithmetic Progressions Ex 9.5
RD Sharma Class 10 Solutions Arithmetic Progressions Exercise 9.5
Question 1.
Find the value of x for which (8x + 4), (6x – 2) and (2x + 7) are in A.P.
Solution:
(8x + 4), (6x – 2) and (2x + 7) are in A.P.
(6x – 2) – (8x + 4) = (2x + 7) – (6x – 2)
⇒ 6x – 2 – 8x – 4 = 2x + 7 – 6x + 2
⇒ -2x – 6 = -4x + 9
⇒ -2x + 4x = 9 + 6
⇒ 2x = 15
Hence x = \(\frac { 15 }{ 2 }\)
Question 2.
If x + 1, 3x and 4x + 2 are in A.P., find the value of x.
Solution:
x + 1, 3x and 4x + 2 are in A.P.
3x – x – 1 = 4x + 2 – 3x
⇒ 2x – 1 = x + 2
⇒ 2x – x = 2 + 1
⇒ x = 3
Hence x = 3
Question 3.
Show that (a – b)², (a² + b²) and (a + b)² are in A.P.
Solution:
(a – b)², (a² + b²) and (a + b)² are in A.P.
If 2 (a² + b²) = (a – b)² + (a + b)²
If 2 (a² + b²) = a² + b² – 2ab + a² + b² + 2ab
If 2 (a² + b²) = 2a² + 2b² = 2 (a² + b²)
Which is true
Hence proved.
Question 4.
The sum of three terms of an A.P. is 21 and the product of the first and the third terms exceeds the second term by 6, find three terms.
Solution:
Let the three terms of an A.P. be a – d, a, a + d
Sum of three terms = 21
⇒ a – d + a + a + d = 21
⇒ 3a = 21
⇒ a = 7
and product of the first and 3rd = 2nd term + 6
⇒ (a – d) (a + d) = a + 6
a² – d² = a + 6
⇒ (7 )² – d² = 7 + 6
⇒ 49 – d² = 13
⇒ d² = 49 – 13 = 36
⇒ d² = (6)²
⇒ d = 6
Terms are 7 – 6, 7, 7 + 6 ⇒ 1, 7, 13
Question 5.
Three numbers are in A.P. If the sum of these numbers be 27 and the product 648, find the numbers.
Solution:
Let the three numbers of an A.P. be a – d, a, a + d
According to the conditions,
Sum of these numbers = 27
a – d + a + a + d = 27
⇒ 3a = 27

Question 6.
Find the four numbers in A.P., whose sum is 50 and in which the greatest number is 4 times the least.
Solution:
Let the four terms of an A.P. be (a – 3d), (a – d), (a + d) and (a + 3d)
Now according to the condition,
Sum of these terms = 50
⇒ (a – 3d) + (a – d) + (a + d) + (a + 3d) = 50
⇒ a – 3d + a – d + a + d + a – 3d= 50
⇒ 4a = 50
⇒ a = \(\frac { 25 }{ 2 }\)
and greatest number = 4 x least number
⇒ a + 3d = 4 (a – 3d)
⇒ a + 3d = 4a – 12d
⇒ 4a – a = 3d + 12d

Question 7.
The sum of three numbers in A.P. is 12 and the sum of their cubes is 288. Find the numbers.
Solution:

Question 8.
Divide 56 in four parts in A.P. such that the ratio of the product of their extremes to the product of their means is 5 : 6. [CBSE 2016]
Solution:


Question 9.
The angles of a quadrilateral are in A.P. whose common difference is 10°. Find the angles.
Solution:
Let the four angles of a quadrilateral which are in A.P., be
a – 3d, a – d, a + d, a + 3d
Common difference = 10°
Now sum of angles of a quadrilateral = 360°
a – 3d + a – d + a + d + a + 3d = 360°
⇒ 4a = 360°
⇒ a = 90°
and common difference = (a – d) – (a – 3d) = a – d – a + 3d = 2d
2d = 10°
⇒ d = 5°
Angles will be
a – 3d = 90° – 3 x 5° = 90° – 15° = 75°
a – d= 90° – 5° = 85°
a + d = 90° + 5° = 95°
and a + 3d = 90° + 3 x 5° = 90° + 15°= 105°
Hence the angles of the quadrilateral will be
75°, 85°, 95° and 105°
Question 10.
Split 207 into three parts such that these are in A.P. and the product of the two smaller parts is 4623. [NCERT Exemplar]
Solution:
Let the three parts of the number 207 are (a – d), a and (a + d), which are in A.P.
Now, by given condition,
⇒ Sum of these parts = 207
⇒ a – d + a + a + d = 207
⇒ 3a = 207
a = 69
Given that, product of the two smaller parts = 4623
⇒ a (a – d) = 4623
⇒ 69 (69 – d) = 4623
⇒ 69 – d = 67
⇒ d = 69 – 67 = 2
So, first part = a – d = 69 – 2 = 67,
Second part = a = 69
and third part = a + d = 69 + 2 = 71
Hence, required three parts are 67, 69, 71.
Question 11.
The angles of a triangle are in A.P. The greatest angle is twice the least. Find all the angles. [NCERT Exemplar]
Solution:
Given that, the angles of a triangle are in A.P.

Question 12.
The sum of four consecutive numbers in A.P. is 32 and the ratio of the product of the first and last terms to the product of two middle terms is 7 : 15. Find the number. [NCERT Exemplar]
Solution:

or, d = ± 2
So, when a = 8, d = 2,
the numbers are 2, 6, 10, 14.
Exercise 9.5
RD Sharma Class 10 Solutions Chapter 9 Arithmetic Progressions Ex 9.5














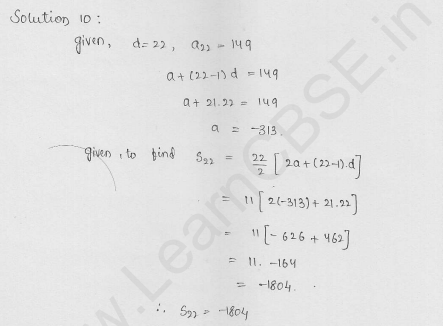





























RD Sharma Class 10 Solutions
- Chapter 9 Arithmetic Progressions Ex 9.1
- Chapter 9 Arithmetic Progressions Ex 9.2
- Chapter 9 Arithmetic Progressions Ex 9.3
- Chapter 9 Arithmetic Progressions Ex 9.4
- Chapter 9 Arithmetic Progressions Ex 9.5