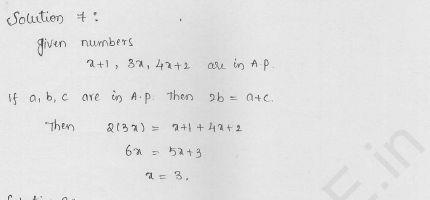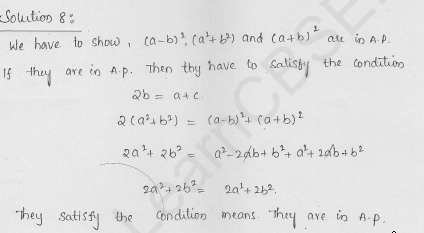RD Sharma Class 10 Solutions Chapter 9 Arithmetic Progressions Ex 9.4
RD Sharma Class 10 Solutions Arithmetic Progressions Exercise 9.4
Question 1.
(i) 10th term of the A.P. 1, 4, 7, 10, ………
(ii) 18th term of the A.P. √2 , 3√2 , 5√2 , ……….
(iii) nth term of the A.P. 13, 8, 3, -2, ……..
(iv) 10th term of the A.P. -40, -15, 10, 35, ……..
(v) 8th term of the A.P. 117, 104, 91, 78, ………..
(vi) 11th term of the A.P. 10.0 , 10.5, 11.0, 11.5, ……….
(vii) 9th term of the A.P. \(\frac { 3 }{ 4 }\) , \(\frac { 5 }{ 4 }\) , \(\frac { 7 }{ 4 }\) , \(\frac { 9 }{ 4 }\) , ………
Solution:




Question 2.
(i) Which term of the A.P. 3, 8, 13, …… is 248 ?
(ii) Which term of the A.P. 84, 80, 76, ….. is 0 ?
(iii) Which term of the A.P. 4, 9, 14, ….. is 254 ?
(iv) Which term of the A.P. 21, 42, 63, 84, ….. is 420 ?
(v) Which term of the A.P. 121, 117, 113, ….. is its first negative term ?
Solution:
(i) A.P. is 3, 8, 13, …, 248
Here first term (a) = 3
and common difference (d) = 8 – 3 = 5



Question 3.
(i) Is 68 a term of the A.P. 7, 10, 13, …… ?
(ii) Is 302 a term of the A.P. 3, 8, 13, ….. ?
(ii) Is -150 a term of the A.P. 11, 8, 5, 2, …… ?
Solution:


Question 4.
How many terms are there in the A.P. ?
(i) 7, 10, 13, … 43
(ii) -1, – \(\frac { 5 }{ 6 }\) , – \(\frac { 2 }{ 3 }\) , – \(\frac { 1 }{ 2 }\) , …….., \(\frac { 10 }{ 3 }\)
(iii) 7, 13, 19, …, 205
(iv) 18, 15\(\frac { 1 }{ 2 }\) , 13, …, -47
Solution:




Question 5.
The first term of an A.P. is 5, the common difference is 3 and the last term is 80; find the number of terms.
Solution:
The first term of an A.P. (a) = 5
and common difference (d) = 3
Last term = 80
Let the last term be nth
an = a + (n – 1) d
⇒ 80 = 5 + (n – 1) x 3
⇒ 80= 5 + 3n – 3
⇒ 3n = 80 – 5 + 3 = 78
⇒ n = 26
Number of terms = 26
Question 6.
The 6th and 17th terms of an A.P. are 19 and 41 respectively, find the 40th term.
Solution:
6th term of A.P. = 19
and 17th term = 41
Let a be the first term, and d be the common difference
We know that

Question 7.
If 9th term of an A.P. is zero, prove that its 29th term is double the 19th term.
Solution:

Question 8.
If 10 times the 10th term of an A.P. is equal to 15 times the 15th term, show that 25th term of the A.P. is zero.
Solution:
Let a, a + d, a + 2d, a + 3d, ……… be an A.P.
an = a + (n – 1) d
Now a10 = a + (10 – 1) d = a + 9d
and a15 = a + (15 – 1) d = a + 14d

Question 9.
The 10th and 18th terms of an A.P. are 41 and 73 respectively. Find 26th term.
Solution:

Question 10.
In a certain A.P. the 24th term is twice the 10th term. Prove that the 72nd term is twice the 34th term.
Solution:
Let a, a + d, a + 2d, a + 3d, …….. be an A.P.
an = a + (n – 1) d
10th (a10) = a + (10 – 1) d = a + 9d
and 24th term (a24) = a + (24 – 1) d = a + 23d
24th term = 2 x 10th term
a + 23d = 2 (a + 9d)
⇒ a + 23d = 2a + 18d
⇒ 2a – a = 23d – 18d
⇒ a = 5d ….(i)
Now 72nd term = a + (72 – 1)d = a + 71d
and 34th term = a + (34 – 1) d = a + 33d
Now a + 71d – 5d + 71d = 76d
and a + 33d = 5d+ 33d = 38d
76d = 2 x 38d
72th term = 2 (34th term) = twice of the 34th term
Hence proved.
Question 11.
The 26th, 11th and last term of an A.P. are 0, 3 and – \(\frac { 1 }{ 5 }\) , respectively. Find the common difference and the number of terms. [NCERT Exemplar]
Solution:
Let the first term, common difference and number of terms of an A.P. are a, d and n, respectively.
We know that, if last term of an A.P. is known, then
l = a + (n – 1) d ……(i)
and nth term of an A.P is


Question 12.
If the nth term of the A.P. 9, 7, 5, … is same as the nth term of the A.P. 15, 12, 9, … find n.
Solution:
In A.P 9, 7, 5, ………
Here first term (a) = 9 and d = 7 – 9 = -2 {or 5 – 7 = -2}
nth term (an) = a + (n – 1) d = 9 + (n – 1) (-2) = 9 – 2n + 2 = 11 – 2n
Now in A.P. 15, 12, 9, …..
Here first term (a) = 15 and (d) = 12 – 15 = -3
nth term (an) = a + (n – 1) d = 15 + (n – 1) x (-3)
The nth term of first A.P. = nth term of second A.P.
11 – 2n = 18 – 3n
⇒ -2n + 3n = 18 – 11
⇒ n = 7
Hence n = 7
Question 13.
Find the 12th term from the end of the following arithmetic progressions :
(i) 3, 5, 7, 9, … 201
(ii) 3, 8, 13,…, 253
(iii) 1, 4, 7, 10, …, 88
Solution:
(i) In the A.P. 3, 5, 7, 9, … 201
First term (a) = 3, last term (l) = 201
and common difference (d) = 5 – 3 = 2
We know that nth term from the last = l – (n – 1 ) d
12th term from the last = 201 – (12 – 1) x 2 = 201 – 11 x 2 = 201 – 22 = 179
(ii) In the A.P. 3, 8, 13, …, 253
First term (a) = 3
Common difference (d) = 8 – 3 = 5
and last term = 253
The nth term from the last = l – (n – 1) d
12th term from the last = 253 – (12 – 1) x 5 = 253 – 11 x 5 = 253 – 55 = 198
(iii) In the A.P. 1, 4, 7, 10, …, 88
First term (a) = 1
Common difference (d) = 4 – 1 = 3
and last term = 88
The nth term from the last = l – (n – 1) d
12th term from the last = 88 – (12 – 1) x 3 = 88 – 11 x 3 = 88 – 33 = 55
Question 14.
The 4th term of an A.P. is three times the first and the 7th term exceeds twice the third term by 1. Find the first term and the common difference.
Solution:

Question 15.
Find the second term and nth term of an A.P. whose 6th term is 12 and the 8th term is 22.
Solution:
In an A.P.
6th term (a6) = 12
and 8th term (a8) = 22
Let a be the first term and d be the common difference, then

Question 16.
How many numbers of two digit are divisible by 3 ?
Solution:
Let n be the number of terms which are divisible by 3 and d are of two digit numbers
Let a be the first term and d be the common difference, then
a = 12, d = 3, last term = 99
an = a + (n – 1) d
99 = 12 + (n – 1) x 3
⇒ 99 = 12 + 3n – 3
⇒ 3n = 99 – 9
⇒ n = 30
Number of terms = 30
Question 17.
An A.P. consists of 60 terms. If the first and the last terms be 7 and 125 respectively, find 32nd term.
Solution:
In an A.P.
n = 60
First term (a) = 7 and last term (l) = 125
Let d be the common difference, then
a60 = a + (60 – 1) d
⇒ 125 = 7 + 59d
⇒ 59d = 125 – 7 = 118
Common difference = 2
Now 32nd term (a32) = a + (32 – 1) d = 7 + 31 x 2 = 7+ 62 = 69
Question 18.
The sum of 4th and 8th terms of an A.P. is 24 and the sum of the 6th and 10th terms is 34. Find the first term and the common difference of the A.P.
Solution:

Question 19.
The first term of an A.P. is 5 and its 100th term is -292. Find the 50th term of this A.P.
Solution:
First term of an A.P. = 5
and 100th term = -292

Question 20.
Find a30 – a20 for the A.P.
(i) -9, -14, -19, -24, …
(ii) a, a + d, a + 2d, a + 3d, …
Solution:

Question 21.
Write the expression an – ak for the A.P. a, a + d, a + 2d, ……
Hence, find the common difference of the A.P. for which
(i) 11th term is 5 and 13th term is 79.
(ii) a10 – a5 = 200
(iii) 20th term is 10 more than the 18th term.
Solution:
In the A.P. a, a + d, a + 2d, …..

Question 22.
Find n if the given value of x is the nth term of the given A.P.

Solution:




Question 23.
The eighth term of an A.P. is half of its second term and the eleventh term exceeds one third of its fourth term by 1. Find the 15th term.
Solution:

Question 24.
Find the arithmetic progression whose third term is 16 and seventh term exceeds its fifth term by 12.
Solution:
Let a, a + d, a + 2d, a + 3d, ………. be the A.P.
an = a + (n – 1) d
But a3 = 16

Question 25.
The 7th term of an A.P. is 32 and its 13th term is 62. Find the A.P. [CBSE 2004]
Solution:
Let a, a + d, a + 2d, a + 3d, be the A.P.
Here a is the first term and d is the common difference
an = a + (n – 1) d
Now a7 = a + (7 – 1) d = a + 6d = 32 ….(i)
and a13 = a + (13 – 1) d = a + 12d = 62 ….(ii)
Subtracting (i) from (ii)
6d = 30
⇒ d = 5
a + 6 x 5 = 32
⇒ a + 30 = 32
⇒ a = 32 – 30 = 2
A.P. will be 2, 7, 12, 17, ………..
Question 26.
Which term of the A.P. 3, 10, 17, … will be 84 more than its 13th term ? [CBSE 2004]
Solution:


Question 27.
Two arithmetic progressions have the same common difference. The difference between their 100th terms is 100, what is the difference between their 1000th terms ?
Solution:

Question 28.
For what value of n, the nth terms of the arithmetic progressions 63, 65, 67,… and 3, 10, 17, … are equal ? (C.B.S.E. 2008)
Solution:
In the A.P. 63, 65, 67, …
a = 63 and d = 65 – 63 = 2
an = a1 + (n – 1) d = 63 + (n – 1) x 2 = 63 + 2n – 2 = 61 + 2n
and in the A.P. 3, 10, 17, …
a = 3 and d = 10 – 3 = 7
an = a + (n – 1) d = 3 + (n – 1) x 7 = 3 + 7n – 7 = 7n – 4
But both nth terms are equal
61 + 2n = 7n – 4
⇒ 61 + 4 = 7n – 2n
⇒ 65 = 5n
⇒ n = 13
n = 13
Question 29.
How many multiples of 4 lie between 10 and 250 ?
Solution:
All the terms between 10 and 250 are multiple of 4
First multiple (a) = 12
and last multiple (l) = 248
and d = 4
Let n be the number of multiples, then
an = a + (n – 1) d
⇒ 248 = 12 + (n – 1) x 4 = 12 + 4n – 4
⇒ 248 = 8 + 4n
⇒ 4n = 248 – 8 = 240
n = 60
Number of terms are = 60
Question 30.
How many three digit numbers are divisible by 7 ?
Solution:
First three digit number is 100 and last three digit number is 999
In the sequence of the required three digit numbers which are divisible by 7, will be between
a = 105 and last number l = 994 and d = 7
Let n be the number of terms, then
an = a + (n – 1) d
994 = 105 + (n – 1) x 7
994 = 105 + 7n – 7
⇒ 7n = 994 – 105 + 7
⇒ 7n = 896
⇒ n = 128
Number of terms =128
Question 31.
Which term of the arithmetic progression 8, 14, 20, 26, … will be 72 more than its 41st term ? (C.B.S.E. 2006C)
Solution:
In the given A.P. 8, 14, 20, 26, …

Question 32.
Find the term of the arithmetic progression 9, 12, 15, 18, … which is 39 more than its 36th term (C.B.S.E. 2006C)
Solution:
In the given A.R 9, 12, 15, 18, …
First term (a) = 9
and common difference (d) = 12 – 9 = 3
and an = a + (n – 1) d
Now a36 = a + (36 – 1) d = 9 + 35 x 3 = 9 + 105 = 114
Let the an be the required term
an = a + (n – 1) d
= 9 + (n – 1) x 3 = 9 + 3n – 3 = 6 + 3n
But their difference is 39
an – a36 = 39
⇒ 6 + 3n – 114 = 39
⇒ 114 – 6 + 39 = 3n
⇒ 3n = 147
⇒ n = 49
Required term is 49th
Question 33.
Find the 8th term from the end of the A.P. 7, 10, 13, …, 184. (C.B.S.E. 2005)
Solution:
The given A.P. is 7, 10, 13,…, 184
Here first term (a) = 7
and common difference (d) = 10 – 7 = 3
and last tenn (l) = 184
Let nth term from the last is an = l – (n – 1) d
a8= 184 – (8 – 1) x 3 = 184 – 7 x 3 = 184 – 21 = 163
Question 34.
Find the 10th term from the end of the A.P. 8, 10, 12, …, 126. (C.B.S.E. 2006)
Solution:
The given A.P. is 8, 10, 12, …, 126
Here first term (a) = 8
Common difference (d) = 10 – 8 = 2
and last tenn (l) = 126
Now nth term from the last is an = l – (n – 1) d
a10 = 126 – (10 – 1) x 2 = 126 – 9 x 2 = 126 – 18 = 108
Question 35.
The sum of 4th and 8th terms of an A.P. is 24 and the sum of 6th and 10th terms is 44. Find the A.P. (C.B.S.E. 2009)
Solution:

Question 36.
Which term of the A.P. 3, 15, 27, 39, …. will be 120 more than its 21st term ? (C.B.S.E. 2009)
Solution:
A.P. is given : 3, 15, 27, 39, …….
Here first term (a) = 3
and c.d. (d) = 15 – 3 = 12
Let nth term be the required term
Now 21st term = a + (n – 1) d = 3 + 20 x 12 = 3 + 240 = 243
According to the given condition,
nth term – 21 st term = 120
⇒ a + (n – 1) d – 243 = 120
⇒ 3 + (n – 1) x 12 = 120 + 243 = 363
⇒ (n – 1) 12 = 363 – 3 = 360
⇒ n – 1 = 30
⇒ n = 30 + 1 = 31
31 st term is the required term
Question 37.
The 17th term of an A.P. is 5 more than twice its 8th term. If the 11th term of the A.P. is 43, find the nth term.[CBSE 2012]
Solution:

Question 38.
Find the number of ail three digit natural numbers which are divisible by 9. [CBSE 2013]
Solution:
First 3-digit number which is divisible by 9 = 108
and last 3-digit number = 999
d= 9
a + (n – 1) d = 999
⇒ 108 + (n – 1) x 9 = 999
⇒ (n – 1) d = 999 – 108
⇒ (n – 1) x 9 = 891
⇒ n – 1 = 99
⇒ n = 99 + 1 = 100
Number of terms = 100
Question 39.
The 19th term of an A.P. is equal to three times its sixth term. If its 9th term is 19, find the A.P. [CBSE 2013]
Solution:

Question 40.
The 9th term of an A.P. is equal to 6 times its second term. If its 5th term is 22, find the A.P. [CBSE 2013]
Solution:
Let a be the first term and d be the common difference and
Tn = a + (n – 1) d

Question 41.
The 24th term of an A.P. is twice its 10th term. Show that its 72nd term is 4 times its 15th term. [CBSE 2013]
Solution:

Hence 72nd term = 4 times of 15th term
Question 42.
Find the number of natural numbers between 101 and 999 which are divisible by both 2 and 5. [CBSE 2014]
Solution:
Numbers divisible by both 2 and 5 are 110, 120, 130, ………. , 990
Here a = 110, x = 120 – 110 = 10
an = 990
As a + (n – 1) d = 990
110 + (n – 1) (10) = 990
(n – 1) (10) = 990 – 110 = 880
n – 1 = 88
n = 88 + 1 = 89
Question 43.
If the seventh term of an AP is \(\frac { 1 }{ 9 }\) and its ninth term is \(\frac { 1 }{ 7 }\) , find its (63) rd term. [CBSE 2014]
Solution:


Question 44.
The sum of 5th and 9th terms of an AP is 30. If its 25th term is three times its 8th term, find the AP. [CBSE 2014]
Solution:

Question 45.
Find where 0 (zero) is a term of the AP 40, 37, 34, 31, …… [CBSE 2014]
Solution:
AP 40, 37, 34, 31, …..
Here a = 40, d = -3
Let Tn = 0
Tn = a + (n – 1) d
⇒ 0 = 40 + (n – 1) (-3)
⇒ 0 = 40 – 3n + 3
⇒ 3n = 43
⇒ n = \(\frac { 43 }{ 3 }\) which is in fraction
There is no term which is 0
Question 46.
Find the middle term of the A.P. 213, 205, 197, …, 37. [CBSE2015]
Solution:

Question 47.
If the 5th term of an A.P. is 31 and 25th term is 140 more than the 5th term, find the A.P. [BTE2015]
Solution:
We know that,
Tn = a + (n – 1 )d
T5 = a + 4d ⇒ a + 4d = 31 ……(i)
and T25 = a + 24d
⇒a + 24d = 140 + T5
⇒ a + 24d = 140 + 31 = 171 …..(ii)
Subtracting (i) from (ii),
20d= 140
and a + 4d = 31
⇒ a + 4 x 7 = 31
⇒ a + 28 = 31
⇒ a = 31 – 28 = 3
a = 3 and d = 7
AP will be 3, 10, 17, 24, 31, ……..
Question 48.
Find the sum of two middle terms of the

Solution:


Question 49.
If (m + 1)th term of an A.P. is twice the (n + 1)th term, prove that (3m + 1)th term is twice the (m + n + 1)th term.
Solution:

Question 50.
If an A.P. consists of n terms with first term a and nth term l show that the sum of the mth term from the beginning and the mth term from the end is (a + l).
Solution:
In an A.P.
Number of terms = n
First term = a
and nth term = l
mth term (am) = a + (m – 1) d
and mth term from the end = l – (m – 1)d
Their sum = a + (m – 1) d + l – (m – 1) d = a + l
Hence proved.
Question 51.
How many numbers lie between 10 and 300, which when divided by 4 leave a remainder 3? [NCERT Exemplar]
Solution:
Here, the first number is 11, which divided by 4 leave remainder 3 between 10 and 300.
Last term before 300 is 299, which divided by 4 leave remainder 3.
11, 15, 19, 23, …, 299
Here, first term (a) = 11,
common difference (d) = 15 – 11 = 4
nth term, an = a + (n – 1 ) d = l [last term]
⇒ 299 = 11 + (n – 1) 4
⇒ 299 – 11 = (n – 1) 4
⇒ 4(n – 1) = 288
⇒ (n – 1) = 72
n = 73
Question 52.
Find the 12th term from the end of the A.P. -2, -4, -6, …, -100. [NCERT Exemplar]
Solution:
Given, A.P., -2, -4, -6, …, -100
Here, first term (a) = -2,
common difference (d) = -4 – (-2)
and the last term (l) = -100.
We know that, the nth term an of an A.P. from the end is an = l – (n – 1 )d,
where l is the last term and d is the common difference. 12th term from the end,
an = -100 – (12 – 1) (-2)
= -100 + (11) (2) = -100 + 22 = -78
Hence, the 12th term from the end is -78
Question 53.
For the A.P.: -3, -7, -11,…, can we find a30 – a20 without actually finding a30 and a20 ? Give reasons for your answer. [NCERT Exemplar]
Solution:
True.
nth term of an A.P., an = a + (n – 1)d
a30 = a + (30 – 1 )d = a + 29d
and a20 = a + (20 – 1 )d = a + 19d …(i)
Now, a30 – a20 = (a + 29d) – (a + 19d) = 10d
and from given A.P.
common difference, d = -7 – (-3) = -7 + 3 = -4
a30 – a20 = 10(-4) = -40 [from Eq- (i)]
Question 54.
Two A.P.s have the same common difference. The first term of one A.P. is 2 and that of the other is 7. The difference between their 10th terms is the same as the difference between their 21st terms, which is the same as the difference between any two corresponding terms. Why? [NCERT Exemplar]
Solution:
Let the same common difference of two A.P.’s is d.
Given that, the first term of first A.P. and second A.P. are 2 and 7 respectively,
then the A.P.’s are 2, 2 + d, 2 + 2d, 2 + 3d, … and 7, 7 + d, 7 + 2d, 7 + 3d, …
Now, 10th terms of first and second A.P.’s are 2 + 9d and 7 + 9d, respectively.
So, their difference is 7 + 9d – (2 + 9d) = 5
Also, 21st terms of first and second A.P.’s are 2 + 20d and 7 + 20d, respectively.
So, their difference is 7 + 20d – (2 + 9d) = 5
Also, if the an and bn are the nth terms of first and second A.P.
Then bn – an = [7 + (n – 1 ) d] – [2 + (n – 1) d = 5
Hence, the difference between any two corresponding terms of such A.P.’s is the same as the difference between their first terms.
Exercise 9.4
RD Sharma Class 10 Solutions
- Chapter 9 Arithmetic Progressions Ex 9.1
- Chapter 9 Arithmetic Progressions Ex 9.2
- Chapter 9 Arithmetic Progressions Ex 9.3
- Chapter 9 Arithmetic Progressions Ex 9.4
- Chapter 9 Arithmetic Progressions Ex 9.5