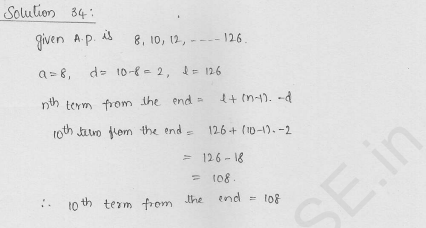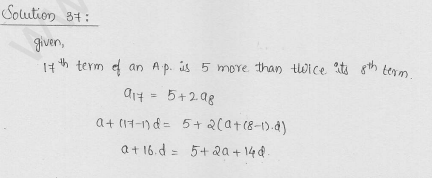RD Sharma Class 10 Solutions Chapter 9 Arithmetic Progressions Ex 9.3
RD Sharma Class 10 Solutions Arithmetic Progressions Exercise 9.3
Question 1.
For the following arithmetic progressions write the first term a and the common difference d :
(i) -5, -1, 3, 7, …………
(ii) \(\frac { 1 }{ 5 }\) , \(\frac { 3 }{ 5 }\) , \(\frac { 5 }{ 5 }\) , \(\frac { 7 }{ 5 }\) , ……
(iii) 0.3, 0.55, 0.80, 1.05, …………
(iv) -1.1, -3.1, -5.1, -7.1, …………..
Solution:
(i) -5, -1, 3, 7, …………


Question 2.
Write the arithmetic progression when first term a and common difference d are as follows:
(i) a = 4, d = -3
(ii) a = -1, d= \(\frac { 1 }{ 2 }\)
(iii) a = -1.5, d = -0.5
Solution:
(i) First term (a) = 4
and common difference (d) = -3
Second term = a + d = 4 – 3 = 1
Third term = a + 2d = 4 + 2 x (-3) = 4 – 6 = -2
Fourth term = a + 3d = 4 + 3 (-3) = 4 – 9 = -5
Fifth term = a + 4d = 4 + 4 (-3) = 4 – 12 = -8
AP will be 4, 1, -2, -5, -8, ……….


Question 3.
In which of the following situations, the sequence of numbers formed will form an A.P. ?
(i) The cost of digging a well for the first metre is ₹ 150 and rises by ₹ 20 for each succeeding metre.
(ii) The amount of air present in the cylinder when a vacuum pump removes each time \(\frac { 1 }{ 4 }\) of the remaining in the cylinder.
(iii) Divya deposited ₹ 1000 at compound interest at the rate of 10% per annum. The amount at the end of first year, second year, third year, …, and so on. [NCERT Exemplar]
Solution:
(i) Cost of digging a well for the first metre = ₹ 150
Cost for the second metre = ₹ 150 + ₹ 20 = ₹ 170
Cost for the third metre = ₹ 170 + ₹ 20 = ₹ 190
Cost for the fourth metre = ₹ 190 + ₹ 20 = ₹ 210
The sequence will be (In rupees)
150, 170, 190, 210, ………..
Which is an A.P.
Whose = 150 and d = 20
(ii) Let air present in the cylinder = 1


(iii) Amount at the end of the 1st year = ₹ 1100
Amount at the end of the 2nd year = ₹ 1210
Amount at the end of 3rd year = ₹ 1331 and so on.
So, the amount (in ₹) at the end of 1st year, 2nd year, 3rd year, … are
1100, 1210, 1331, …….
Here, a2 – a1 = 110
a3 – a2 = 121
As, a2 – a1 ≠ a3 – a2, it does not form an AP
Question 4.
Find the common difference and write the next four terms of each of the following arithmetic progressions :
(i) 1, -2, -5, -8, ……..
(ii) 0, -3, -6, -9, ……
(iii) -1, \(\frac { 1 }{ 4 }\) , \(\frac { 3 }{ 2 }\) , ……..
(iv) -1, – \(\frac { 5 }{ 6 }\) , – \(\frac { 2 }{ 3 }\) , ………..
Solution:





Question 5.
Prove that no matter what the real numbers a and b are, the sequence with nth term a + nb is always an A.P. What is the common difference ?
Solution:
an = a + nb
Let n= 1, 2, 3, 4, 5, ……….
a1 = a + b
a2 = a + 2b
a3 = a + 3b
a4 = a + 4b
a5 = a + 5b
We see that it is an A.P. whose common difference is b and a for any real value of a and b
as a2 – a1 = a + 2b – a – b = b
a3 – a2 = a + 3b – a – 2b = b
a4 – a3 = a + 4b – a – 3b = b
and a5 – a4 = a + 5b – a – 4b = b
Question 6.
Find out which of the following sequences are arithmetic progressions. For those which are arithmetic progressions, find out the common difference.

Solution:






Question 7.
Find the common difference of the A.P. and write the next two terms :
(i) 51, 59, 67, 75, …….
(ii) 75, 67, 59, 51, ………
(iii) 1.8, 2.0, 2.2, 2.4, …….
(iv) 0, \(\frac { 1 }{ 4 }\) , \(\frac { 1 }{ 2 }\) , \(\frac { 3 }{ 4 }\) , ………..
(v) 119, 136, 153, 170, ………..
Solution:




Exercise 9.3
RD Sharma Class 10 Solutions
- Chapter 9 Arithmetic Progressions Ex 9.1
- Chapter 9 Arithmetic Progressions Ex 9.2
- Chapter 9 Arithmetic Progressions Ex 9.3
- Chapter 9 Arithmetic Progressions Ex 9.4
- Chapter 9 Arithmetic Progressions Ex 9.5