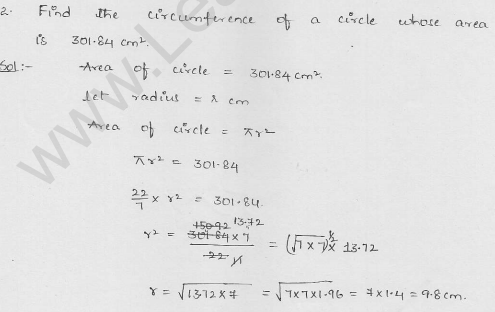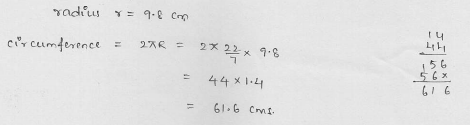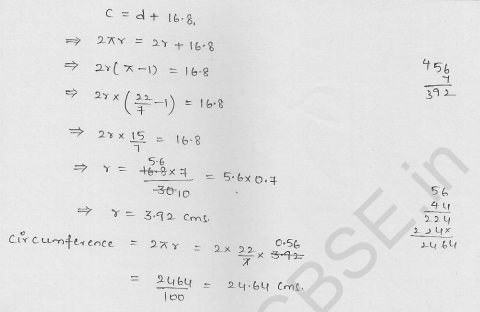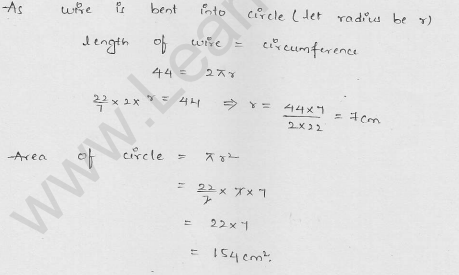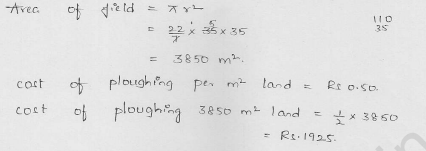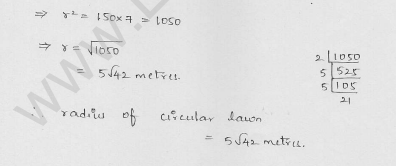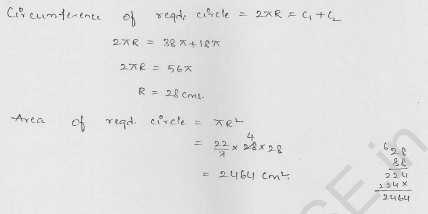RD Sharma Class 10 Solutions Chapter 15 Areas related to Circles
RD Sharma Class 10 Solutions Areas related to Circles Exercise 15.1
Question 1.
Find the circumference and area of a circle of radius 4.2 cm.
Solution:
Radius of a circle = 4.2 cm

Question 2.
Find the circumference of a circle whose area is 301.84 cm2.
Solution:
Area of a circle = 301.84 cm2
Let r be the radius, then πr2 = 301.84

Question 3.
Find the area of a circle whose circumference is 44 cm.
Solution:
Circumference of a circle = 44 cm
Let r be the radius,
then 2πr = circumference

Question 4.
The circumference of a circle exceeds the diameter by 16.8 cm. Find the circumference of the circle. (C.B.S.E. 1996)
Solution:
Let r be the radius of the circle
∴ Circumference = 2r + 16.8 cm
⇒ 2πr = 2r + 16.8
⇒ 2πr – 2r = 16.8

Question 5.
A horse is tied to a pole with 28 m long string. Find the area where the horse can graze. (Take π = 22/7)
Solution:
Radius of the circle (r) = Length of the rope = 28 m .
Area of the place where the horse can graze

Question 6.
A steel wire when bent in the form of a square encloses an area of 121 cm2. If the same wire is bent in the form of a circle, find the area of the circle. (C.B.S.E. 1997)
Solution:
Area of square formed by a wire =121 cm2
∴ Side of square (a) = \(\sqrt { Area } \) = \(\sqrt { 121 } \) = 11 cm Perimeter of the square = 4 x side = 4 x 11 = 44 cm
∴Circumference of the circle formed by the wire = 44cm
Let r be the radius

Question 7.
The circumference of two circles are in the ratio 2 : 3. Find the ratio of their areas.
Solution:
Let R and r be the radii of two circles and their ratio between them circumference = 2 : 3

Question 8.
The sum of radii of two circles is 140 cm and the difference of their circumferences is 88 cm. Find the diameters of the circles.
Solution:
Let R and r be the radii of two circles Then R + r = 140 cm …….(i)
and difference of their circumferences


Question 9.
Find the radius of a circle whose circumference is equal to the sum of the circumferences of two circles of radii 15 cm and 18 cm. [NCERT Exemplar]
Solution:
Let the radius of a circle be r.
Circumference of a circle = 2πr
Let the radii of two circles are r1 and r2 whose
values are 15 cm and 18 cm respectively.
i.e., r1 = 15 cm and r2 = 18 cm
Now, by given condition,
Circumference of circle = Circumference of first circle + Circumference of second circle
⇒ 2πr = 2π r1 + 2πr2 =
⇒ r = r1 + r2
⇒ r = 15 + 18
∴ r = 33 cm
Hence, required radius of a circle is 33 cm.
Question 10.
The radii of two circles are 8 cm and 6 cm respectively. Find the radius of the circle having its area equal to the sum of the areas of the two circles.
Solution:
Radius of first circle (r1) = 8 cm
and radius of second circle (r2) = 6 cm


Question 11.
The radii of two circles are 19 cm and 9 cm respectively. Find the radius and area of the circle which has its circumference equal to the sum of the circumferences of the two circles.
Solution:
Radius of the first circle (r1) = 19 cm
and radius of the second circle (r2) = 9 cm S
um of their circumferences = 2πr1 + 2πr2
= 2π (r1 + r2) = 2π (19 + 9) cm
= 2π x 28 = 56π cm
Let R be the radius of the circle whose circumference is the sum of the circumferences of given two circles, then

Question 12.
The area of a circular playground is 22176 m2. Find the cost of fencing this ground at the rate of ₹50 per metre. [NCERT Exempiar]
Solution:
Given, area of a circular playground = 22176 m2

![]()
Question 13.
The side of a square is 10 cm. Find the area of circumscribed and inscribed circles.
Solution:
ABCD is a square whose each side is 10 cm
∴ AB = BC = CD = DA = 10 cm
AC and BD are its diagonals


Question 14.
If a square is inscribed in a circle, find the ratio of the areas of the circle and the square.
Solution:
Let r be the radius of the circle a be the side of the square


Question 15.
The area of a circle inscribed in an equilateral triangle is 154 cm2. Find the perimeter of the triangle. (Use π = 22/7 and \(\sqrt { 3 } \) = 1.73)
Solution:
Area of the inscribed circle of ΔABC = 154 cm2


Question 16.
A field is in the form of a circle. A fence is to be erected around the field. The cost of fencing would be ₹2640 at the rate of ₹12 per metre. Then, the field is to be thoroughly ploughed at the cost of ₹0.50 per m2. What is the amount required to plough the field ? (Take π = 22/7)
Solution:
Cost of the fencing the circular field = ₹2640
Rate = ₹12 per metre 2640
∴ Circumference = \((\frac { 2640 }{ 12 } )\) = 220 m
Let r be the radius of the field, then = 2πr = 220

Question 17.
A park is in the form of a rectangle 120 m x 100 m. At the centre of the park there is a circular lawn. The area of park excluding lawn is 8700 m2. Find the radius of the circular lawn. (Use π = 22/7).
Solution:
Area of the park excluding lawn = 8700 m2
Length of rectangular park = 120 m
and width = 100 m

∴ Area of lawn = l x b
= 120 x 100 m2 = 12000 m2
Let r be the radius of the circular lawn, then area of lawn = πr2

Question 18.
A car travels 1 kilometre distance in which each wheel makes 450 complete revolutions. Find the radius of the its wheels.
Solution:
Distance covered by the car in 450 revolutions = 1 km = 1000 m
∴ Distance covered in 1 revolution = \((\frac { 1000 }{ 450 } )\)
= \((\frac { 20 }{ 9 } )\) m

Question 19.
The area of enclosed between the concentric circles is 770 cm2. If the radius of the outer circle is 21 cm, find the radius of the inner circle.
Solution:
Area of enclosed between two concentric circles = 770 cm2
Radius of the outer circle (R) = 21 cm

Question 20.
An archery target has three regions formed by the concentric circles as shown in the figure. If the diameters of the concentric circles are in the ratio 1:2:3, then find the ratio of the areas of three regions.[NCERT Exemplar]

Solution:
Let the diameters of concentric circles be k, 2k , 3k

Question 21.
The wheel of a motor cycle is of radius 35 cm. How many revolutions per minute must the wheel make so as to keep a speed of 66 km/hr? [NCERT Exemplar]
Solution:
Given, radius of wheel, r = 35 cm
Circumference of the wheel = 2πr
= 2 x \((\frac { 22 }{ 7 } )\) x 35 = 220 cm
But speed of the wheel = 66 kmh-1
= \((\frac { 66 x 1000 }{ 60 } )\) m/ mm
= 1100 x 100 cm min-1
= 110000 cm min-1
∴ Number of revolutions in 1 min
= \((\frac { 110000 }{ 220 } )\)= 500 revolution
Hence, required number of revolutions per minute is 500.
Question 22.
A circular pond is 17.5 m in diameter. It is surrounded by a 2 m wide path. Find the cost of constructing the path at the rate of ₹25 per m2. [NCERT Exemplar]
Solution:
Given that, a circular pond is surrounded by a wide path.
The diameter of circular pond = 17.5 m

Question 23.
A circular park is surrounded by a rod 21 m wide. If the radius of the park is 105 m, find the area of the road. [NCERT Exemplar]
Solution:
Given that, a circular park is surrounded by a road.
Width of the road = 21 m
Radius of the park (r1) = 105 m

.’. Radius of whole circular portion (park + road),
re = 105 + 21 = 126 m
Now, area of road = Area of whole circular portion – Area of circular park
= πr2 – πr2 [∵ area of circle = πr2]

Question 24.
A square of diagonal 8 cm is inscribed in a circle. Find the area of the region lying outside the circle and inside the square. [NCERT Exemplar]
Solution:
Let the side of a square be a and the radius of circle be r.
Given that, length of diagonal of square = 8 cm

Question 25.
A path of 4 m width runs round a semicircular grassy plot whose circumference is 81 \((\frac { 5 }{ 7 } )\)m. Find:
(i) the area of the path
(ii) the cost of gravelling the path at the rate of ₹1.50 per square metre
(iii) the cost of turfing the plot at the rate of 45 paise per m2.
Solution:
Width of path around the semicircular grassy plot = 4 m
Circumference of the plot = 81 \((\frac { 5 }{ 7 } )\)m
= \((\frac { 572 }{ 7 } )\) m
Let r be the radius of the plot, then


Question 26.
Find the area enclosed between two concentric circles of radii 3.5 cm and 7 cm. A third concentric circle is drawn outside the 7 cm circle, such that the area enclosed between it and the 7 cm circle is same as that between the two inner circles. Find the radius of the third circle correct to one decimal place.
Solution:
Radius of first circle (r1) = 3.5 cm
Radius of second circle (r2) = 7 cm


Question 27.
A path of width 3.5 m runs around a semicircular grassy plot whose perimeter is 72 m. Find the area of the path. (Use π = 22/7) [CBSE 2015]
Solution:
Perimeter of semicircle grassy plot = 72 m

Let r be the radius of the plot

![]()
Question 28.
A circular pond is of diameter 17.5 m. It is surrounded by a 2 m wide path. Find the cost of constructing the path at the rate of ₹25 per square metre (Use π = 3.14) [CBSE 2014]
Solution:
Diameter of circular pond (d) = 17.5 m
Radius (r) =\((\frac { 1725 }{ 2 } )\) = 8.75 m
Width of path = 2m
∴ Radius of outer cirlce (R) = 8.75 + 2 = 10.75 m
Area of path = (R2 – r2)π
= [(10.75)2 – (8.75)2](3.14)
= 3.14(10.75 + 8.75) (10.75 – 8.75)
= 3.14 x 19.5 x 2 = 122.46 m2
Cost of 1 m2 for constructing the path ₹25 m2
∴ Total cost = ₹ 122.46 x 25 = ₹3061.50
Question 29.
The outer circumference of a circular race-track is 528 m. The track is everywhere 14 m wide. Calculate the cost of levelling the track at the rate of 50 paise per square metre (Use π= 22/7).
Solution:
Let R and r be the radii of the outer and inner of track.
Outer circumference of the race track = 528 m


Question 30.
A road which is 7 m wide surrounds a circular park whose circumference is 352 m. Find the area of the road.
Solution:
Width of the road = 7 m

Circumference of the park = 352 m
Let r be the radius, then 2πr = 352


Question 31.
Prove that the area of a circular path of uniform width hsurrounding a circular region of radius r is πh(2r + h).
Solution:
Radius of inner circle = r
Width of path = h
∴ Outer radius (R) = (r + h)
∴ Area of path = πR2 – πr2
= π {(r + h)2 – r2}
= π {r2 + h2 + 2rh – r2}
= π {2rh + h2}
= πh (2r + h) Hence proved.
Exercise 15.1
RD Sharma Class 10 Solutions
- Chapter 15 Areas related to Circles Ex 15.1
- Chapter 15 Areas related to Circles Ex 15.2
- Chapter 15 Areas related to Circles Ex 15.3
- Chapter 15 Areas related to Circles Ex 15.4
RD Sharma Class 10 Solutions Chapter 15 Areas related to Circles Exercise 15.1
Q1 Q2 Q3 Q4 Q5 Q6 Q7 Q8 Q9 Q10 Q11 Q12 Q13 Q14 Q15 Q16 Q17 Q18 Q19
RD Sharma Class 10 Solutions Chapter 15 Areas related to Circles Exercise 15.2
Q1 Q2 Q3 Q4 Q5 Q6 Q7 Q8 Q9 Q10 Q11 Q12 Q13 Q14 Q15 Q16 Q17 Q18 Q19 Q20
RD Sharma Class 10 Solutions Chapter 15 Areas related to Circles Exercise 15.3
RD Sharma Class 10 Solutions Chapter 15 Areas related to Circles Exercise 15.4
Q1 Q2 Q3 Q4 Q5 Q6 Q7 Q8 Q9 Q10 Q11 Q12 Q13 Q14 Q15 Q16 Q17 Q18
More Resources For Class 10
RD Sharma Class 10 SolutionsAreas related to CirclesClass 10 Maths Sample Papers