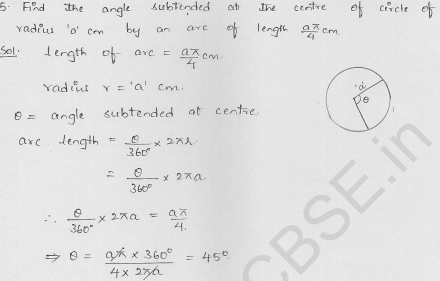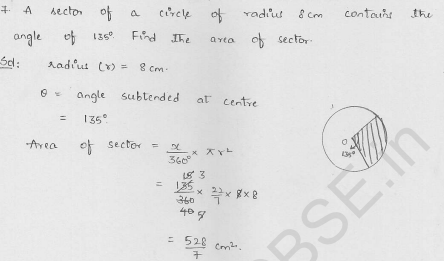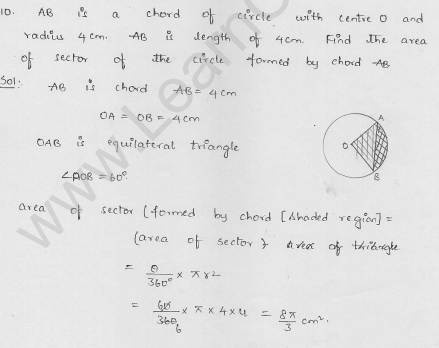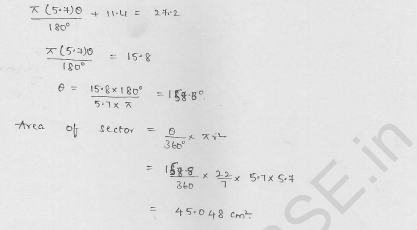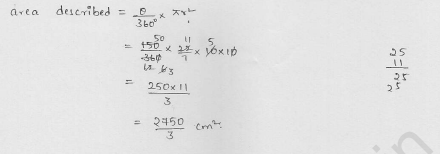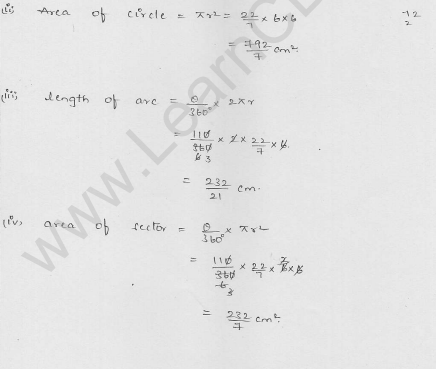RD Sharma Class 10 Solutions Areas related to Circles Ex 15.2

RD Sharma Class 10 Solutions Areas related to Circles Ex 15.2

RD Sharma Class 10 Solutions Areas related to Circles Exercise 15.2

Question 1.
Find, in terms of π the length of the arc that subtends an angle of 30° at the centre of a circle of radius 4 cm.
Solution:
Radius of the circle (r) = 4 cm
Angle at the centre subtended an arc = 30°

Question 2.
Find the angle subtended at the centre of a circle of radius 5 cm by an arc of length \((\frac { 5\pi }{ 3 } \) cm.
Solution:
Radius of the circle (r) = 5 cm 571
Length of arc = \(\frac { 5\pi }{ 3 }\) cm
Let θ be the angle subtended by the arc, then

Question 3.
An arc of length 20tc cm subtends an angle of 144° at the centre of a circle. Find the radius of the circle.
Solution:
Length of an arc = 20π cm
Angle subtended by the arc = 144°
Let r be the radius of the circle, then

Question 4.
An arc of length 15 cm subtends an angle of 45° at the centre of a circle. Find in terms of π ; the radius of the circle.
Solution:
Length of arc = 15 cm
Angle subtended at the centre = 45°
Let r be the radius of the circle, then

Question 5.
Find the angle subtended at the centre of a circle of radius ‘a’  by an arc of length \((\frac { a\pi }{ 4 } )\)  cm.
Solution:
Radius of the circle (r) = a cm
Length of arc = \(\frac { a\pi }{ 4 }\)   cm
Let θ be the angle subtended by the arc at the centre, then

Question 6.
A sector of a circle of radius 4 cm contains an angle of 30°. Find the area of the sector.
Solution:
Radius of the sector of a circle (r) = 4 cm
Angle at the centre (θ) = 30°

Question 7.
A sector of a circle of radius 8 cm contains an angle of 135°. Find the area of the sector.
Solution:
Radius of the sector of the circle (r) = 8 cm
Angle at the centre (θ) = 135°

Question 8.
The area of a sector of a circle of radius 2 cm is 7 is cm². Find the angle contained by the sector.
Solution:
Area of the sector of a circle =π cm²
Radius of the circle (r) = 2 cm
Let 0 be the angle at the centre, then

Question 9.
The area of a sector of a circle of radius 5 cm is 5π cm². Find the angle contained by the sector.
Solution:
Area of the sector of a circle = 5π cm²
Radius of the circle (r) = 5 cm
Let 9 be the angle at the centre, then

Question 10.
Find the area of the sector of a circle of radius 5 cm, if the corresponding arc length is 3.5 cm. [NCERT Exemplar]
Solution:
Let the central angle of the sector be θ.
Given that, radius of the sector of a circle (r) = 5 cm
and arc length (l) = 3.5 cm

Question 11.
In a circle of radius 35 cm, an arc subtends an angle of 72° at the centre. Find the length of the arc and area of the sector.
Solution:
Radius of the circle (r) = 25 cm
Angle at the centre (θ) = 72°

Question 12.
The perimeter of a sector of a circle of radius 5.7 m is 27.2 m. Find the area of the sector.
Solution:
Radius of the circle (r) = 5.7 m
Perimeter of the sector = 27.2 m
Length of the arc = Perimeter – 2r
= (27.2 – 2 x 5.7) m
= 27.2 – 11.4 = 15.8 m
Let θ be the central angle, then

Question 13.
The perimeter of a certain sector of a circle of radius 5.6 cm is 27.2 m. Find the area of the sector.
Solution:
Radius of the sector (r) = 5.6 cm
and perimeter of the sector = 27.2 cm
∴ Length of arc = Perimeter – 2r
= 27.2 – 2 x 5.6
= 27.2- 11.2= 16.0 cm
∴ θ be the angle at the centre, then

Question 14.
A sector is cut-off from a circle of radius 21 cm. The angle of the sector is 120°. Find the length of its arc and the area.
Solution:
Radius of the sector of a circle (r) = 21 cm
Angle at the centre = 120°

Question 15.
The minute hand of a clock is \(\sqrt { 21 } \)  cm long, Find the area described by the minute hand on the face of the clock between 7.00 A.M. and 7.05 A.M.
Solution:
Length of minute hand of a clock (r) = \(\sqrt { 21 }\)  cm
Period = 7 a.m. to 7.05 a.m. 5 minutes

Question 16.
The minute hand of a clock is 10 cm long. Find the area of the face of the clock described by the minute hand between 8.00 A.M. and 8.25 A.M.
Solution:
Length of minute hand of a clock (r) = 10 cm
Period = 8 A.M. to 8.25 A.M. = 25 minutes

Question 17.
The sector of 56° cut out from a circle contains area 4.4 cm², Find the radius of the circle.
Solution:
Area of a sector = 4.4 cm²
Central angle = 56°                                        ‘
Let r be the radius of the sector of the circle, then

Question 18.
Area of a sector of central angle 200° of a circle s 770²cm. Find the length of the corresponding are of this sector.
Solution:
Let the radius of the sector AOBA be r.
Given that, Central angle of sector AOBA = θ = 200°
and area of the sector AOBA = 770 cm²

Question 19.
The length of minute hand of a clock is 5 cm. Find the area swept by the minute hand during the time period 6:05 am and 6:40 am.           [NCERT Exemplar]
Solution:
We know that, in 60 min, minute hand revolving = 360°
In 1 min, minute hand revolving = \(\frac { 360\circ }{ 60\circ }\)

Question 20.
The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 5 minutes. [CBSE 2013]
Solution:
Length of minute hand (r)= 14 cm
Area swept by the minute hand in 5 minutes

Question 21.
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find (0 the length of the arc (ii) area of the secter formed by the arc. (Use π = 22/7) [CBSE 2013]
Solution:
Radius of a circle (r) = 21 cm
Angle at the centre = 60°

Question 22.
From a circular piece of cardboard of radius 3 cm two sectors of 90° have been cut off. Find the perimeter of the remaining portion nearest hundredth centimeters (Take π = 22/7).
Solution:
Radius of the circular piece of cardboard (r) = 3 cm

∴ Two sectors of 90° each have been cut off
∴ We get a semicular cardboard piece
∴ Perimeter of arc ACB

Question 23.
The area of a sector is one-twelfth that of the complete circle. Find the angle of the sector.
Solution:
Let r be the radius of the circle and 0 be the central angle of the sector of the circle Then area of circle = πr²

Question 24.
AB is a chord of a circle with centre O and radius 4 cm. AB is of length 4 cm. Find the area of the sector of the circle formed by the chord AB.
Solution:
Radius of the circle with centre O (r) = 4 cm
Length of chord AB = 4 cm

Question 25.
In a circle of radius 6 cm, a chord of length 10 cm makes an angle of 110° at the centre of the circle. Find
(i)  the circumference of the circle,
(ii) the area of the circle,
(iii) the length of the arc AB,
(iv) the area of the sector OAB.
Solution:
Radius of the circle (r) = 6 cm
Length of chord = 10 cm
and central angle (θ) =110°

Question 26.
Figure, shows a sector of a circle, centre O, containing an angle θ°. Prove that :

Solution:
Radius of the circle = r
Arc AC subtends ∠θ at the centre of the
circle. OAB is a right triangle
In the right ΔOAB,

Question 27.
Figure, shows a sector of a circle of radius r cm containing an angle θ°. The area of the sector is A cm² and perimeter of the sector is 50 cm. Prove that

Solution:
Radius of the sector of the circle = r cm
and angle at the centre = 0
Area of sector OAB = A cm²
and perimeter of sector OAB = 50 cm

Exercise 15.2

RD Sharma Class 10 Solutions

• Chapter 15 Areas related to Circles Ex 15.1
• Chapter 15 Areas related to Circles Ex 15.2
• Chapter 15 Areas related to Circles Ex 15.3
• Chapter 15 Areas related to Circles Ex 15.4