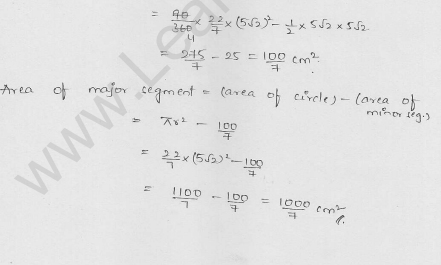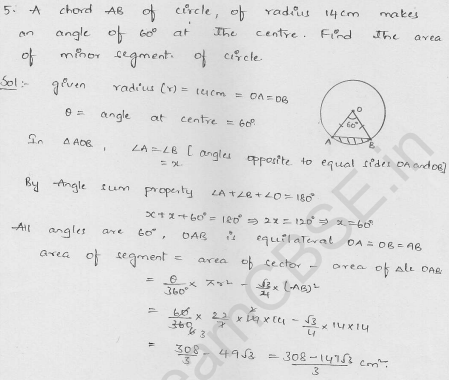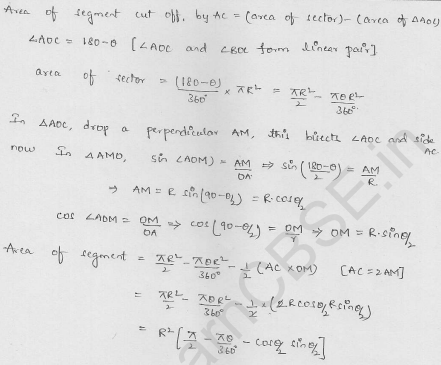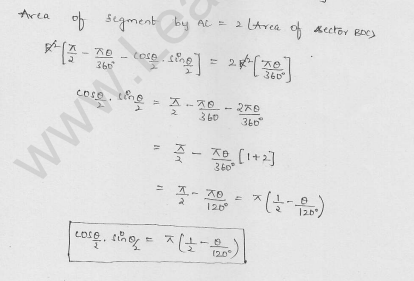RD Sharma Class 10 Solutions Areas related to Circles Ex 15.3

RD Sharma Class 10 Solutions Areas related to Circles Ex 15.3

RD Sharma Class 10 Solutions Areas related to Circles Exercise 15.3

Question 1.
AB is a chord of a circle with centre O and radius 4 cm. AB is of length 4 cm and divides the circle into two segments. Find the area of the minor segment.
Solution:
Radius of the circle (r) = 4 cm
Length of the chord AB = 4 cm
∴  In ΔOAB
OA = OB = AB    (each = 4 cm)

Question 2.
A chord PQ of length 12 cm subtends an angle of 120° at the centre of a circle. Find the area of the minor segment cut off by the chord PQ.
Solution:
Length of chord PQ = 12 cm
Angle at the centre (θ) = 120°
∵  Draw OD ⊥ DQ
which bisects PQ at D and also bisects ∠POQ

Question 3.
A chord of a circle of radius 14 cm makes a right angle at the centre. Find the areas of the minor and major segments of the circle.
Solution:
Radius of the circle (r) = 14 cm
Angle at the centre (θ) = 90°

Question 4.
A ehord 10 cm long is drawn in a circle whose radius is 5\(\sqrt { 2 } \)
cm. Find area of both the segments. (Take π = 3.14).
Solution:
Radius of the circle (r) = 5\(\sqrt { 2 } \)  cm
And length of chord AB = 10 cm

Question 5.
A chord AB of a circle, of radius 14 cm makes an angle of 60° at the centre of the circle. Find the area of the minor segment of the circle. (Use π = 22/7)
Solution:
Radius of the circle (r) – 14 cm
Angle at the centre subtended in the fnui
AB = 60°

Question 6.
Find the area of the minor segment of a circle of radius 14 cm, when the angle of the corresponding sector is 60°. [NCERT Exemplar]
Solution:
Given that, radius of circle (r) = 14 cm

Question 7.
A chord of a circle of radius 20 cm subtends an angle of 90° at the centre. Find the area of the corresponding major segment of the circle. (Use π = 3.14) [NCERT Exemplar]
Solution:
Let AB be the chord of a circle of radius 10 cm,
with O as the centre of the circle.

Question 8.
The radius of a circle with centre O is 5 cm (see figure). Two radii OA and OB are drawn at right angles to each other. Find the areas of the segments made by the chord AB (Take π = 3.14).

Solution:
Radius of the circle (r) = 5 cm
∵   OA and OB are at right angle
∴ ∠AOB = 90°
∵  Chord AB makes two segments which are minor segment and major segment Now area of minor segment

Question 9.
AB is the diameter of a circle, centre O. C is a point on the circumference such that ∠COB = 0. The area of the minor segment cut off by AC is equal to twice the area of the sector BOC. Prove that

Solution:

Question 10.
A chord of a circle subtends an angle of 0 at the centre of the circle. The area of the minor segment cut off by the chord is one eighth of the area of the circle. Prove that

Solution:
Let chord AB subtends angle 0 at the centre
of a circle with radius r
Now area of the circle = nr¹
and area of the minor segment ACB

Exercise 15.3

RD Sharma Class 10 Solutions

• Chapter 15 Areas related to Circles Ex 15.1
• Chapter 15 Areas related to Circles Ex 15.2
• Chapter 15 Areas related to Circles Ex 15.3
• Chapter 15 Areas related to Circles Ex 15.4