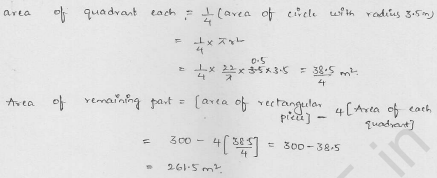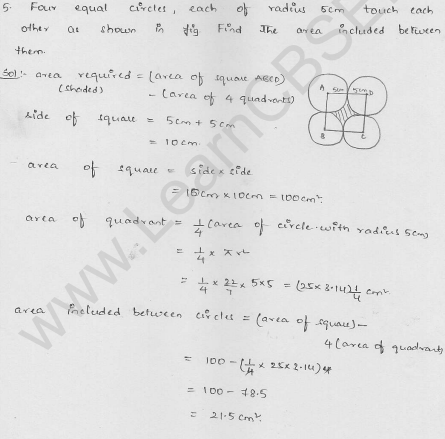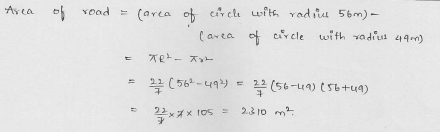RD Sharma Class 10 Solutions Areas related to Circles Ex 15.4
RD Sharma Class 10 Solutions Areas related to Circles Exercise 15.4
Question 1.
A plot is in the form of a rectangle ABCD having semi-circle on BC as shown in the figure. If AB = 60 m and BC = 28 m, find the area of the plot.

Solution:
Plot is formed of a rectangle ABCD and one semicircle on BC as diameter
∴ AB (l) = 60 m,
BC (b) = 28 m
∴ Radius of semicircle (r) = \(\frac { 1 }{ 2 }\) BC
= \(\frac { 1 }{ 2 }\) x 28 = 14m
Area of plot = area of rectangle ABCD + area of semicircle


Question 2.
A play ground has the shape of a rectangle, with two semi-circles on its smaller sides as diameters, added to its outside. If the sides of the rectangle are 36 m and 24.5 m, find the area of the playground. (Take π = 22/7).
Solution:
Length of rectangle (l) = 36 m 49
and width (b) = 24.5 = \(\frac { 49 }{ 2 }\) m

Question 3.
Find the area of the circle in which a square of area 64 cm2 is inscribed. (Use π = 3.14)
Solution:
Area of square = 64 cm²
∴ Side of square = \(\sqrt { Area } \) = \(\sqrt { 64 } \) = 8 cm
∵ The square in inscribed in the circle
∴ Radius of the circle will be = \(\frac { 1 }{ 2 }\) diagonal of
the square (r)=\(\frac { 1 }{ 2 }\) x \(\sqrt { 2 } \)a = \(\frac { 1 }{ 2 }\) x \(\sqrt { 2 } \) x 8 cm = 4\(\sqrt { 2 } \)
∴ Area of the circle = πr²
= 3.14 x (4\(\frac { 1 }{ 2 }\) x \(\sqrt { 2 } \) x 8 cm = 4\(\sqrt { 2 } \))² cm²
= 3.14 x 32 = 100.48 cm²
Question 4.
A rectangular piece is 20 m long and 15 m wide. From its four corners, quadrants of radii 3.5 m have been cut. Find the area of the remaining part.
Solution:
Length of rectangular piece (l) = 20 m
and width (b) = 15m

Radius of each quadrant (r) = 3.5 m = \(\frac { 7 }{ 2 }\) m
Now area of the rectangle = l x b = 20 x 15 = 300 m²
and area of 4 quadrants = 4 x \(\frac { 1 }{ 4 }\) πr²

Question 5.
In the figure, PQRS is a square of side 4 cm. Find the area of the shaded square.

Solution:
Side of the square PQRS (a) = 4 cm
∴ Area of total square = a² = 4×4=16 cm²
Radius of each of the four quadrants at the corners = 1 cm

Question 6.
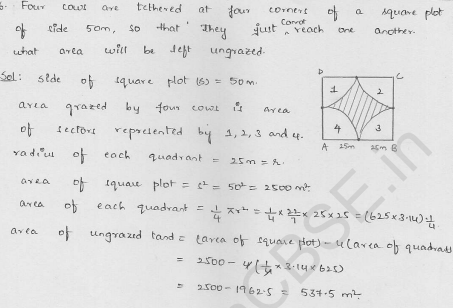
Four cows are tethered at four corners of a square plot of side 50 m, so that they just cannot reach one another. What area will be left ungrazed ? (See figure)

Solution:
side of square (a) = 50 m
∴ Area of the square field = a² = (50)² m² = 2500 m²
Radius of each quadrant (r) = \(\frac { 50 }{ 2 }\) = 25 m

Question 7.
A cow is tied with a rope of length 14 m at the corner of a rectangular field of dimensions 20 m x 16 m, find the area of the field in which the cow can graze. [NCERT Exemplar]
Solution:
Let ABCD be a rectangular field of dimensions 20 m x 16 m.
Suppose, a cow is tied at a point A. Let length of rope AE = 14m =r (say).

Question 8.
A calf is teid with a rope of length 6 m at the corner of a square grassy lawn of side 20 m. If the length of the rope is increased by 5.5 m, find the increase in area of the grassy lawn in which the calf can graze. [NCERT Exemplar]
Solution:
Let the calf be tied at the corner A of the square lawn.

Then, the increase in area = Difference of the two sectors of central angle 90° each and radii 11.5 m (6 m + 5.5 m) and 6 m, which is the shaded region in the figure.

Question 9.
A square water tank has its side equal to 40 m. There are four semi-circular grassy plots all round it. Find the cost of turfing the plot at ?1.25 per square metre (Take π = 3.14).
Solution:
Side of square tank (a) = 40 m
Radius of each semicircular grassy plots = \(\frac { 40 }{ 2 }\) = 20

Question 10.
A rectangular park is 100 m by 50 m. It is surrounded by semi-circular flower beds all round. Find the cost of levelling the semi-circular flower beds at 60 paise per square metre. (Use π = 3.14).
Solution:
Length of rectangular park (l) = 100 m
and width (b) = 50 m

Radius of each semicircular beds along the
lengths side (R) = \(\frac { 100 }{ 2 }\) = 50 m
and radius of each semicircular beds along
the width side (r) = \(\frac { 50 }{ 2 }\) = 25 m

Question 11.
The inside perimeter of a running track (shown in the figure) is 400 m. The length of each of the straight portion is 90 m and the ends are semi-circles. If the track is everywhere 14 m wide, find the area of the track. Also find the length of the outer running track.

Solution:


Question 12.
Find the area of the figure, in square cm, correct to one place of decimal. (Take π = 22/7).

Solution:
Join AD
ABCD is a square whose each side = 10 cm

Area of square = a² = (10)² = 100 cm²
Area of half semicircle whose radius is \(\frac { 10 }{ 2 }\) = 5


Question 13.
In the figure, from a rectangular region ABCD with AB = 20 cm, a right triangle AED with AE = 9 cm and DE = 12 cm, is cut off. On the other end, taking BC as diameter, a semicircle is added on outside the region. Find the area of the shaded region. (Use π = 22/7). [CBSE 2014]

Solution:
AB = 20 cm, AE = 9 cm, DE = 12 cm
∠AED = 90°


Question 14.
From each of the two opposite corners of a square of side 8 cm, a quadrant of a cirlce of radius 1.4 cm is cut. Another circle of diameter 4.2 cm is also cut from the centre as shown in the figure. Find the area of the remaining (shaded) portion of the square. (Use π = 22/7). [CBSE 2010]

Solution:
Side of a square ABCD = 8 cm


Question 15.
In the figure, ABCD is a rectangle with AB = 14 cm and BC = 7 cm. Taking DC, BC and AD as diameters, three semi¬circles are drawn as shown in the figure. Find the area of the shaded region.

Solution:
In the figure, ABCD is a rectangle AB = 14 cm abd BC = 7 cm

Two semicircles are draw on AD and BC as diameter and thid semicircle is drawn on Cd as diameter
Now area of rectangle ABCD = l x b = 14 x 7 = 98 cm²
Area of two semicircles on AD and BC

Question 16.
In the figure, ABCD is a rectangle, having AB = 20 cm and BC = 14 cm. Two sectors of 180° have been cut off. Calculate :
(i) the area of the shaded region.
(ii) the length of the boundary of the shaded region.

Solution:
ABCD is a rectangle whose Length AB = 20 cm
and width BC = 14 cm
∴ Area of the rectangle = l x b = 20 x 14 = 280 cm²

Question 17.
In the figure, the square ABCD is divided into five equal parts, all having same area. The central part is circular and the lines AE, GC, BF and HD lie along the diagonals AC and BD of the square. If AB = 22 cm, find :
(i) the circumference of the central part.
(ii) the perimeter of the part ABEF.

Solution:
Side of the square ABCD = 22 cm
∴ Area = (side)² = (22)² = 484 cm²
∵ The squre is divided into 5 parts equal in area
∴ Area of each part = \(\frac { 484 }{ 5 }\) cm²

Question 18.
In the given figure, Find the area of the shaded region. (Use π = 3.14). [CBSE 2015]

Solution:
Side of large square = 14 cm
Radius of each semicircle = \(\frac { 4 }{ 2 }\) = 2 cm
Side of square = 4 cm
Area of square = 4 x 4=16 cm²
∴ Area of semicircles = 4 x \(\frac { 1 }{ 2 }\) πr²
= 2 x 3.14 x 2 x 2
= 8 x 3.14
= 25.12 cm²
∴ Area of shaded region = Area of large square – Area of central portion
= (14)2-(16+ 25.12) cm²
= 196-41.12 cm²
= 154.88 .cm²
Question 19.
In the Figure, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the
(i) quadrant OACB
(ii) shaded region.

Solution:
Radius of outer quadrant (R) = 3.5 cm
and radius of inner quadrant = 2 cm
∴ Area of shaded portion
= Area of outer quadrant – area of inner quadrant


Question 20.
In the figure, a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 21 cm, find the area of the shaded region.[CBSE 2013]

Solution:
In the figure, OPQ is a quadrant in which
OABC is a square OA = 21 cm
Join OB,


Question 21.
In the figure, OABC is a square of side 7 cm. If OAPC is a quadrant of a cirice with centre O, then find the area of the shaded region. (Use π = 22/7) [CBSE 2012]

Solution:
In square OABC, whose side is 7 cm, OAPC
is a quadrant
Area of square = (side)²
= (7)² = 49 cm²
and radius of quadrant = 7 cm

Question 22.
In the figure, OE = 20 cm. In sector OSFT, square OEFG is inscribed. Find the area of the shaded region.

Solution:
In the figure OSFT is a quadrant and OEFG
is a square inscribed in it
The side of the square is OE = 20 cm


Question 23.
Find the area of the shaded region in the figure, if AC = 24 cm, BC = 10 cm and O is the centre of the circle. (Use π = 3.14)

Solution:
In right AABC
AB²=AC² + BC² (Pythagoras Theorem)
= (24)²+ (10)²
= 576 + 100 = 676
= (26)²
∴ AB = 26 cm
∴ Diameter of circle = 26 cm
and radius (r)= \(\frac { 26 }{ 2 }\) = 13 cm
Now area of shaded portion
= Area of semicircle – area of right triangle ABC

Question 24.
A circle is inscribed in an equilateral triangle ABC is side 12 cm, touching its sides (see figure). Find the radius of the inscribed circle and the area of the shaded part.

Solution:
Each side of the equilateral triangle ABC (a) = 12 cm

Question 25.
In the figure, an equilateral triangle ABC of side 6 cm has been inscribed in a circle. Find the area of the shaded region. (Take π = 3.14)

Solution:

Question 26.
A circular field has a perimeter of 650 m. A square plot having its vertices on the circumference of the field is marked in the field. Calculate the area of the square plot.
Solution:
Perimeter of the circular field = 650 m

Question 27.
Find the area of a shaded region in the figure, where a circular arc of radius 7 cm has been drawn with vertex A of an equilateral triangle ABC of side 14 cm as centre, (use π = 22/7 and \(\sqrt { 3 } \) = 1.73) [CBSE 2015]

Solution:
Radius of circular arc (r) = 7 cm
and side of equilateral AABC (a) = 14 cm and each angle = 60°

Area of shaded region
=Area of circle + Area of equilateral triangle – 2 area of sector EAF

Question 28.
A regular hexagon is inscribed in a circle. If the area of hexagon is 24\(\sqrt { 3 } \) cm², find the area of the circle. (Use π = 3.14) [CBSE 2015]
Solution:
A regular hexagon ABCDEF is inscribed in a circle
Area of hexagon = 24 \(\sqrt { 3 } \) cm²
Let r be the radius of circle
∴ Side of regular hexagon = r
Area of equilateral ΔOAB = \(\frac { \sqrt { 3 } }{ 3 }\) r² sq. units

Question 29.
ABCDEF is a regular hexagon with centre O (see figure). If the area of triangle OAB is 9 cm², find the area of :
(i) the hexagon and
(ii) the circle in which the hexagon is inscribed.

Solution:
O is the centre of the regular hexagon ABCDEF and area of the AOAB = 9 cm²
∵ By joining the vertices of the hexagon with O,
(i) We get 6 equal equilateral triangles
∴ Area of hexagon = 9 cm² x 6 = 54 cm²
(ii) Radius of the circle when this hexagon is inscribed in it will be = OB =AB =r

Question 30.
Four equal circles, each of radius 5 cm, touch each other as shown in the figure. Find the area included between them. (Take π = 3.14).

Solution:
Radius of each circle = 5 cm
∵ The four circles touch eachother externally
∴ By joining their centres, we get a square whose side will be 5 + 5 = 10 cm

Now area of square so formed = a² = (10)² = 100 cm²
and area of 4 quadrants = 4 x \(\frac { 1 }{ 4 }\) πr²= πr²
= 3.14 x (5)2 cm² = 3.14 x 25 cm² = 78.5 cm²
∴ Area of the part included between the circles
= 100 – 78.5
= 21.5 cm²
Question 31.
Four equal circles, each of radius ‘a’ touch each other. Show that the area between them is \(\frac { 6 }{ 7 }\)a² . (Take π = \(\frac { 22 }{ 7 }\)
Solution:
Four circles each of radius ‘a’ touch each other at A, B, C and D respectively.
Their centes are P, Q, R and S respectively
By joining PQ, QR, RS, SD


Question 32.
A child makes a poster on a chart paper drawing a square ABCD of side 14 cm. She draws four circles with centre A, B, C and D in which she suggests different ways to save energy. The circles are drawn in such a way that each circle touches externally two of the three remaining circles in the given figure. In the shaded region she write a message ‘Save Energy’. Find the perimeter and area of the shaded region. (Use π = 22/7) [CBSE 2015]

Solution:
Radius of circular arc (r) = 7 cm
Side of square ABCD (a) = 14 cm


Question 33.
The diameter of a coin is 1 cm (see figure). If four such coins be placed on a table so that the rim of each touches that of the other two, find the area of the shaded region (Take π = 3.1416).

Solution:
Diameter of each coin = 1 cm
∴ Radius (r) = \(\frac { 1 }{ 2 }\) cm = 0.5 cm


Question 34.
Two circular pieces of equal radii and maximum area, touching each other are cut out from a rectangular card board of dimensions 14 cm x 7 cm. Find the area of the remaining card board. (Use π = 22/7) [CBSE 2013]
Solution:
Length of rectangle = 14 cm
and breadth = 7 cm

Question 35.
In the figure, AB and CD are two diameters of a circle perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region.

Solution:
Radius of larger circle (R) = 7 cm
and radius of smaller circle (r) =\(\frac { 7 }{ 2 }\) cm
Area of shaded portion = Area of larger circle – area of smaller circle

Question 36.
In the figure, PSR, RTQ and PAQ are three semi-circles of diameters 10 cm, 3 cm and 7 cm respectively. Find the perimeter of the shaded region. [CBSE 2014]

Solution:
Radius of larger semicircle (r1) =\(\frac { 10 }{ 2 }\) = 5 cm
Radius of large semicircle = (r2) = \(\frac { 7 }{ 2 }\) cm
Radius of small semicircle (r3) = \(\frac { 3 }{ 2 }\) cm

Question 37.
In the figure, two circles with centres A and B touch each other at the point C. If AC = 8 cm and AB = 3 cm, find the area of the shaded region.

Solution:
In the figure, two circles with centres A and B touch each-other internally at C
AC = 8 cm and AB = 3 cm
∴ BC = 8 – 3 = 5 cm
∴ Radius of bigger circle (R) = 8 cm
and of smaller circle (r) = 5 cm
∴ Area of shaded portion =Area of bigger circle – area of smaller circle

Question 38.
In the figure, ABCD is a square of side 2a. Find the ratio between
(i) the circumferences
(ii) the areas of the incircle and the circum- circle of the square.

Solution:
A square ABCD is inscribed a circle
The side of the square = 2a
and one circle is inscribed in the square ABCD
Now diameter of the outer circle is AC


Question 39.
In the figure, there are three semicircles, A, B and C having diameter 3 cm each, and another semicircle E having a circle D with diameter 4.5 cm are shown. Calculate :
(i) the area of the shaded region
(ii) the cost of painting the shaded region at the rate of 25 paise per cm², to the nearest rupee.

Solution:



Question 40.
In the figure, ABC is a right-angled triangle, ∠B = 90°, AB = 28 cm and BC = 21 cm. With AC as diameter a semicircle is drawn and with BC as radius a quarter circle is drawn. Find the area of the shaded region correct to two decimal places.

Solution:
In right ΔABC,
AB = 28 cm, BC = 21 cm


Question 41.
In the figure, O is the centre of a circular arc and AOB is a straight line. Find the perimeter and the area of the shaded region correct to one decimal place. (Take π = 3.142)

Solution:
A semicircle is drawn on the diameter AB
ΔACB is drawn in this semicircle in right ΔACB
AC = 12 cm and BC = 16 cm


Question 42.
In the figure, the boundary of the shaded region consists of four semi-circular arcs, the smallest two being equal. If the diameter of the largest is 14 cm and of the smallest is 3.5 cm, find
(i) the length of the boundary,
(ii) the area of the shaded region.

Solution:
Diameter of the biggest semicircle = 14 cm 14
∴ Radius (R) = \(\frac { 14 }{ 2 }\) = 7 cm
Diameter of the small semicircle = 7 cm 7
∴ Radius (r1) = \(\frac { 7 }{ 2 }\) cm
and diameter of each smaller circles = 3.5 cm

Question 43.
In the figure, AB = 36 cm and M is mid¬point of AB. Semi-circles are drawn on AB, AM and MB as diameters. A circle with centre C touches all the three circles. Find the area of the shaded region.

Solution:
In the figure, there are three semicircles one bigger and two smaller There is one small circle also
Now diameter of bigger semicircle = 36 cm
∴ Radius (R) = \(\frac { 36 }{ 2 }\) = 18 cm
and diameter of each smaller semicircle = 18 cm


Question 44.
In the figure, ABC is a right angled triangle in which ∠A = 90°, AB = 21 cm and AC = 28 cm. Semi-circles are described on AB, BC and AC as diameters. Find the area of the shaded region.

Solution:
In the figure, ABC is a right triangle in a semicircle ∠A = 90°, AB = 21 cm and AC = 28 cm

Semicircles are drawn on BC and AC as diameters
In right ΔABC
BC² = AB²+AC² (Pythagoras Theorem)
= 21²+ 28²
= 441 + 784= 1225 = (35)²
∴ BC = 35 cm
Now radius of bigger semicircle (R) = \(\frac { 35 }{ 2 }\) cm,
of semicircle at AB = \(\frac { 21 }{ 2 }\) cm and of
semicircle on AC = \(\frac { 28 }{ 2 }\) cm = 14 cm
Now area of shaded portion
= Area of semicircle on AB as diameter + area of semicircle on AC as diameter + area of ΔABC – area of semicircle on BC as diameter

Question 45.
In the figure, shows the cross-section of railway tunnel. The radius OA of the circular part is 2 m. If ∠AOB = 90°, calculate :
(i) the height of the tunnel
(ii) the perimeter of the cross-section
(iii) the area of the cross-section.

Solution:
Radius of the circular part of the tunnel = 2 m
i.e. OA = OB = 2 m
and ∠AOB = 90°
OD ⊥ AB
∴ D in mid-point of AB
∴ In right ΔAOB,


Question 46.
In the figure, shows a kite in which BCD is the shape of a quadrant of a circle of radius 42 cm. ABCD is a square and ΔCEF is an isosceles right angled triangle whose equal sides are 6 cm long. Find the area of the shaded region.

Solution:
ABCD is a square with side = 42 cm
BCD is a quadrant in which ∠BCD = 90° and radius = 42 cm
ΔCEF is an isosceles right triangle in which CE = CF = 6 cm

Question 47.
In the figure, ABCD is a trapezium of area 24.5 cm2. In it, AD || BC, ∠DAB = 90°, AD = 10 cm and BC = 4 cm. If ABE is a quadrant of a circle, find the area of the shaded region. (Take π – (22/7). [ cbse2014]

Solution:
In the figure, ABCD is a trapezium
Area = 24.5 cm2, AD || BC
∠DAB = 90°, AD = 10 cm BC = 4 cm


Question 48.
In the figure, ABCD is a trapezium with AB || DC, AB = 18 cm, DC = 32 cm and the distance between AB and DC is 14 cm. Circles of equal radii 7 cm with centres A, B, C and D have been drawn. Then, find the area of the shaded region of the figure. (Use π = 22/7). [CBSE 2014]

Solution:
In trapezium ABCD
AB || DC
AB = 18 cm, DC = 32 cm Height = 14 cm
Radius of each at the corner of trapezium = 7 cm


Question 49.
From a thin metallic piece, in the shape of a trapezium ABCD, in which AB || CD and ∠BCD = 90°, a quarter circle BEFC is removed (see figure). Given AB = BC = 3.5 cm and DE = 2 cm, calculate the area of the remaining piece of the metal sheet.

Solution:
ABCD is a trapezium in shape in which
AB || CD and ∠BCD = 90°
AB = BC = 3.5 cm, DE = 2 cm
∴ DC = DE + EC = DE + BC = 2 + 3.5 = 5.5 cm
Now area of trapezium ABCD = \(\frac { 1 }{ 2 }\) (AB + CD) x BC (∵ BC is height)


Question 50.
In the figure, ABC is an equilateral triangle of side 8 cm. A, B and C are the centres of circular arcs of radius 4 cm. Find the area of the shaded region correct upto 2 decimal places. (Take π = 3.142
and \(\sqrt { 3 } \) = 1.732).

Solution:
In the figure, ABC is an equilateral triangle with 8 cm as side with centres A, B and C,
circular arcs drawn of radius 4 cm
Each side of ΔABC = 8 cm


Question 51.
Sides of a triangular field are 15 m, 16 m and 17 m. With the three corners of the field a cow, a buffalo and a horse are tied separately with ropes of length 7 m each to graze in the field. Find the area of the field which cannot be grazed by three animals. (NCERT Exemplar)
Solution:
Given that, a triangular field with the three comers of the field a cow, a buffalo and a horse are tied separately with ropes. So, each animal grazed the field in each corner of triangular field as a sectorial form.
Given, radius of each sector (r) = 7m





Question 52.
In the given figure, the side of a square is 28 cm, and radius of each circle is half of the length of the side of the square where O and O’ are centres of the circles. Find the area of shaded region. [CBSE 2017]

Solution:

Question 53.
In a hospital used water is collected in a cylindrical tank of diameter 2 m and height 5 m. After recycling, this water is used to irrigate a park to hospital whose length is 25 m and breadth is 20 m. If tank is filled completely then what will be the height of standing water used for irrigating the park? [CBSE 2017]
Solution:
Diameter of cylinder (d) = 2 m
Radius of cylinder (r) = 1 m
Height of cylinder (H) = 5 m
Volume of cylindrical tank, Vc = = πr²H = π X (1) 2 X 5= 5πm
Length of the park (L) = 25 m
Now water from the tank is used to irrigated the park. So, volume of cylindrical tank = Volume of water in the park.
⇒ 5π = 25 x 20 x h
⇒ 5π/25 x 20 = h
⇒ h = π/100 m
⇒ h = 0.0314 m
Through recycling of water, better use of the natural resource occurs without wastage. It helps in reducing and preventing pollution.
It thus helps in conserving water. This keeps the greenery alive in urban areas like in parks gardens etc.
Exercise 15.4
RD Sharma Class 10 Solutions
- Chapter 15 Areas related to Circles Ex 15.1
- Chapter 15 Areas related to Circles Ex 15.2
- Chapter 15 Areas related to Circles Ex 15.3
- Chapter 15 Areas related to Circles Ex 15.4