NCERT Exemplar Class 11 Maths Chapter 6 Linear Inequalities are part of NCERT Exemplar Class 11 Maths. Here we have given NCERT Exemplar Class 11 Maths Chapter 6 Linear Inequalities.
NCERT Exemplar Class 11 Maths Chapter 6 Linear Inequalities
Q1. \(\frac { 4 }{ x+1 } \le 3\le \frac { 6 }{ x+1 } \)

Q2. \(\frac { |x-2|-1 }{ |x-2|-2 } \le 0 \)
Sol: Let |x-2| = y
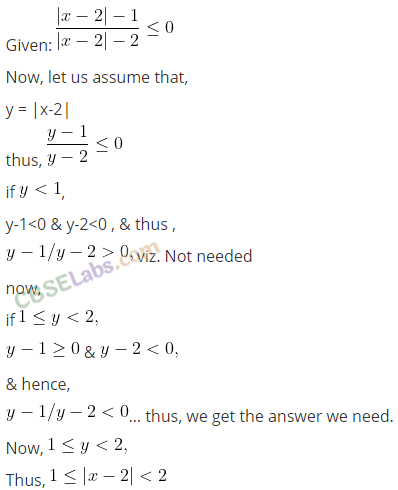

Q3. \(\frac { 1 }{ |x|-3 } \le \frac { 1 }{ 2 } \)
Sol: We have \(\frac { 1 }{ |x|-3 } \le \frac { 1 }{ 2 } \)

Q4. |x-1|≤ 5, |x| ≥ 2
Sol: |x-1|≤ 5
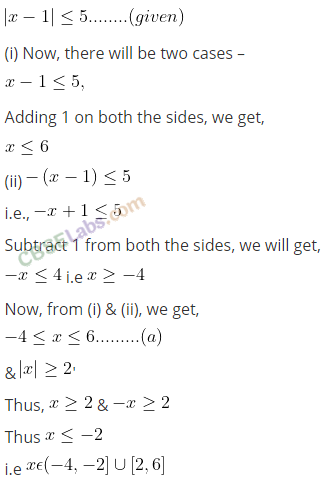
Q5. \(-5\le \frac { 2-3x }{ 4 } \le 9 \)
Sol: we have \(-5\le \frac { 2-3x }{ 4 } \le 9 \)

Q6. 4x + 3≥2x + 17, 3x – 5 < -2.
Sol: We have 4x + 3≥2x + 17

Q7. A company manufactures cassettes. Its cost and revenue functions are C(x) = 26000 + 30x and R(x) = 43x, respectively, where x is the number of cassettes produced and sold in a week How many cassettes must be sold by the company to realise some profit?
Sol. Cost function: C(x) = 26000 + 3Ox Revenue function: R(x) = 43x For profit, R(x) > C(x)
⟹ 26000 + 30x < 43x
⟹43x – 30x > 26000
⟹ 13x> 26000
⟹ x > 2000
Hence, more than 2000 cassettes must be produced to get profit.
Q8. The water acidity in a pool is considered normal when the average pH reading of three daily measurements is between 8.2 and 8.5. If the first two pH readings are 8.48 and 8.35, find the range of pH value for the third reading that will result in the acidity level being normal.
Sol: Given, first pH value = 8.48
And second pH value = 8.35
Let third pH value be x.
Since it is given that average pH value lies between 8.2 and 8.5, we get

Q9. A solution of 9% acid is to be diluted by adding 3% acid solution to it. The resulting mixture is to be more than 5% but less than 7% acid. If there is 460 litres of the 9% solution, how many litres of 3% solution will have to be added?
Sol: Let x Lof 3% solution be added to 460 L of 9% solution of acid.
Then, total quantity of mixture = (460 + x) L

Q10. A solution is to be kept between 40°C and 45°C. What is the range of temperature in degree Fahrenheit, if the conversion formula is F= 9/5 C + 32?
Sol. Let the required temperature be x° F

Q11. The longest side of a triangle is twice the shortest side and the third side is 2 cm longer than the shortest side. If the perimeter of the triangle is more than 166 cm then find the minimum length of the shortest side.
Sol: Let the length of shortest side be x cm.
According to the given information,
Longest side = 2 x Shortest side = 2x cm
And third side = 2 + Shortest side = (2 + x) cm
Perimeter of triangle = x + 2x + (x + 2) = 4x + 2
But it is given that,
Perimeter > 166 cm
=> 4x + 2 > 166 => 4x> 166-2 => 4x>164
x>164/4 =41 cm
Hence, the minimum length of shortest side is 41 cm.
Q12. In drilling world’s deepest hole it was found that the temperature T in degree Celsius, jc km below the earth’s surface was given by T = 30 + 25 (x – 3), 3 ≤ x≤ At what depth will the temperature be between 155°C and 205°C?

Q13. \(\frac { 2x+1 }{ 7x-1 } >5,\frac { x+7 }{ x-8 } >2 \)


Q14. Find the linear inequalities for which the shaded region in the given figure is the solution set.
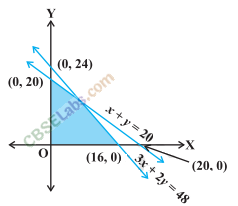
Sol: We observe that the shaded region and the origin are on the same side of the line 3x + 2y = 48.
For (0, 0), we have 3(0) + 2(0) – 48 < 0. So, the shaded region satisfies the inequality 3x + 2y≤ 48.
Also, the shaded region and the origin are on the same side of the line x+y = 20.
For (0,0), we have 0 + 0 – 20 < 0. So, the shaded region satisfies the inequality x +y ≤ 20.
Also, the shaded region lies in the first quadrant. So, x ≥0,y≥0.
Thus, the linear inequation corresponding to the given solution set are 3x + 2y ≤ 48, x + y ≤ 20 and x ≥ 0, y ≥0.
Q15Find the linear inequalities for which the shaded region in the given figure is the solution set.
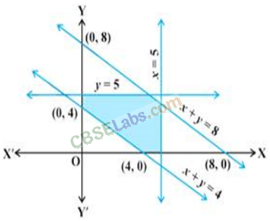
Sol: We observe that the shaded region and the origin are on the same side of the linex+y = 8.
For (0,0), we have 0 + 0 – 8 < 0. So, the shaded region satisfies the inequality x + 2≤8.
The shaded region and the origin are on the opposite side of the line x+y = 4.
For (0,0), we have 0 + 0 – 4 < 0. So, the shaded region satisfies the inequality x + 2≥4.
Further, the shaded region and the origin are on the same side of the lines x = 5 andy = 5.
So, it satisfies the inequality x ≤ 5 andy < 5.
Also, the shaded region lies in the first quadrant. So, x > 0, y > 0.
Thus, the linear inequation comprising the given solution set are: x+y≥4;x+y≤ 8;x≤ 5;y < 5;x≥ 0 andy ≥ 0.
Q16. Show that the following system of linear inequalities has no solution: x + 2y≤3, 3x + 4y> 12,x≥0,y≥ 1
Sol: We have x + 2y ≤ 3, 3x + 4y > 12, x > 0, y ≥ 1
Now let’s plot lines x + 2y = 3, 3x + 4y = 12, x = 0 and y = 1 in coordinate plane.
Line x + 2y = 3 passes through the points (0, 3/2) and (3, 0).
Line 3jc + 4y = 12 passes through points (4, 0) and (0, 3).
For (0, 0), 0 + 2(0) – 3 < 0.
Therefore, the region satisfying the inequality x + 2y ≤ 3 and (0,0) lie on the same side of the line x + 2y = 3.
For (0, 0), 3(0) + 4(0)- 12 ≤0.
Therefore, the region satisfying the inequality 3x + 4y ≥ 12 and (0, 0) lie on the opposite side of the line 3x + 4y = 12.
The region satisfying x > 0 lies to the right hand side of the y-axis.
The region satisfying y > 1 lies above the line y = 1.
These regions are plotted as shown in the following figure
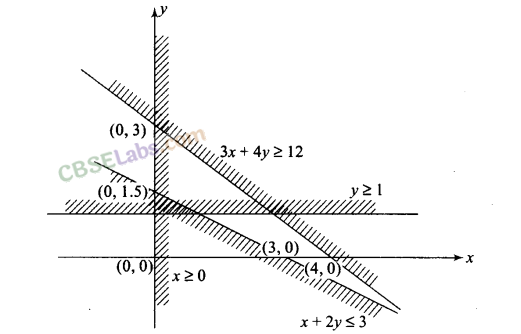
It is clear from the graph that the Shaded portions do not have common region. So, solution set is null set.
Q17. Solve the following system of linear inequalities:
3x+2y≥24,3x+y≤ 15,x≥4
Sol: We have, 3x + 2y ≥24,
3x +y ≤ 15, x ≥ 4
Now let’s plot lines 3x + 2y = 24, 3x + y = 15 and x = 4 on the coordinate plane.
Line 3x + 2y = 24 passes through the points (0, 12) and (8, 0).
Line 3x+y = 15 passes through points (5,0) and (0, 15).
Also line x = 4 is passing through the point (4, 0) and vertical.
For (0, 0), 3(0) + 2(0) – 24 < 0.
Therefore, the region satisfying the inequality 3x + 2y≥ 24 and (0, 0) lie on the opposite of the line 3x + 2y = 24.
For (0), 3(0) + (0) – 15 ≤ 0.
Therefore, the region satisfying the inequality 3x +y ≤ 15 and (0,0) lie on the same side of the line 3x +y = 15.
The region satisfying x ≥ 4 lies to the right hand side of the line x = 4.
These regions are plotted as shown in the following figure
It is clear from the graph that there is no common region corresponding to these inequalities.

Hence, the gi ven system of inequalities has no solution.
Q18. Show that the solution set of the following system of linear inequalities is an unbounded region:
2x +y ≥ 8, x + 2y > 10, x ≥ 0, y ≥ 0
Sol: We have 2x+y≥8,x + 2y> 10, x ≥ 0, y ≥ 0
Line 2x + y = 8 passes through the points (0, 8) and (4, 0).
Line x + 2y = 10 passes through points (10, 0) and (0, 5).\
For (0, 0), 2(0) + (0) – 8 < 0.
Therefore, the region satisfying the inequality 2x+y ≥ 8 and (0, 0) lie on the opposite side of the line 2x +y = 8.
For (0,0), (0) + 2(0)- 10 <0.
Therefore, the region satisfying the inequality x + 2y≥ 10 and (0,0) lie on the opposite side of the line x + 2y = 10.
Also, for x ≥ 0, y ≥0, region lies in the first quadrant.
The common region is plotted as shown in the following figure.
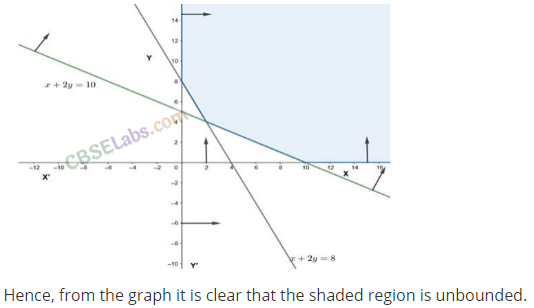
NCERT Exemplar Class 11 Maths Solutions
- Chapter 1 Sets
- Chapter 2 Relations and Functions
- Chapter 3 Trigonometric Functions
- Chapter 4 Principle of Mathematical Induction
- Chapter 5 Complex Numbers and Quadratic Equations
- Chapter 6 Linear Inequalities
- Chapter 7 Permutations and Combinations
- Chapter 8 Binomial Theorem
- Chapter 9 Sequence and Series
- Chapter 10 Straight Lines
- Chapter 11 Conic Sections
- Chapter 12 Introduction to Three-Dimensional Geometry
- Chapter 13 Limits and Derivatives
- Chapter 14 Mathematical Reasoning
- Chapter 15 Statistics
- Chapter 16 Probability
NCERT Exemplar ProblemsMathsPhysicsChemistryBiology</
We hope the NCERT Exemplar Class 11 Maths Chapter 6 Linear Inequalities help you. If you have any query regarding NCERT Exemplar Class 11 Maths Chapter 6 Linear Inequalities, drop a comment below and we will get back to you at the earliest.