NCERT Exemplar Class 11 Maths Chapter 4 Principle of Mathematical Induction

NCERT Exemplar Class 11 Maths Chapter 4 Principle of Mathematical Induction are part of NCERT Exemplar Class 11 Maths. Here we have given NCERT Exemplar Class 11 Maths Chapter 4 Principle of Mathematical Induction.

NCERT Exemplar Class 11 Maths Chapter 4 Principle of Mathematical Induction

Short Answer Type Questions
Q1. Give an example of a statement P(n) which is true for all n≥ 4 but P(l), P(2) and P(3) are not true. Justify your answer.

Sol. Consider the statement P(n): 3n < n!

For n = 1, 3 x 1 < 1!, which is not true
For n = 2, 3 x 2 < 2!, which is not true
For n = 3, 3 x 3 < 3!, which is not true
For n = 4, 3 x 4 < 4!, which is true
For n = 5, 3 x 5 < 5!, which is true

Q2. Give an example of a statement P(n) which is true for all Justify your answer.

Instruction for Exercises 3-16: Prove each of the statements in these Exercises by the Principle of Mathematical Induction.

Q3. 4ⁿ – 1 is divisible by 3, for each natural number
Sol: Let P(n): 4ⁿ – 1 is divisible by 3 for each natural number n.
Now, P(l): 4¹ – 1 = 3, which is divisible by 3 Hence, P(l) is true.
Let us assume that P(n) is true for some natural number n = k.
P(k): 4^k – 1 is divisible by 3
or               4^k – 1 = 3m, m∈ N  (i)
Now, we have to prove that P(k + 1) is true.
P(k+ 1): 4^k+1 – 1
= 4^k-4-l
= 4(3m + 1) – 1  [Using (i)]
= 12 m + 3
= 3(4m + 1), which is divisible by 3 Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction P(n) is true for all natural numbers n.

Q4. 2³ⁿ – 1 is divisible by 7, for all natural numbers
Sol: Let P(n): 2³ⁿ – 1 is divisible by 7
Now, P( 1): 2³ — 1 = 7, which is divisible by 7.
Hence, P(l) is true.
Let us assume that P(n) is true for some natural number n = k.
P(k): 2^3k – 1 is divisible by 7.
or               2^3k -1 = 7m, m∈ N  (i)
Now, we have to prove that P(k + 1) is true.
P(k+ 1): 2^3(k+1)– 1
= 2^3k.2³– 1
= 8(7 m + 1) – 1
= 56 m + 7
= 7(8m + 1), which is divisible by 7.
Thus, P(k + 1) is true whenever P(k) is true.
So, by the principle of mathematical induction P(n) is true for all natural numbers n.

Q5. n³ – 7n + 3 is divisible by 3, for all natural numbers
Sol: Let P(n): n³ – 7n + 3 is divisible by 3, for all natural numbers n.
Now P(l): (l)³ – 7(1) + 3 = -3, which is divisible by 3.
Hence, P(l) is true.
Let us assume that P(n) is true for some natural number n = k.
P(k) = K³ – 7k + 3 is divisible by 3
or K³ – 7k + 3 = 3m, m∈ N         (i)
Now, we have to prove that P(k + 1) is true.
P(k+ 1 ):(k + l)³ – 7(k + 1) + 3
= k³ + 1 + 3k(k + 1) – 7k— 7 + 3 = k³ -7k + 3 + 3k(k + l)-6
= 3m + 3[k(k+l)-2]  [Using (i)]
= 3[m + (k(k + 1) – 2)], which is divisible by 3 Thus, P(k + 1) is true whenever P(k) is true.
So, by the principle of mathematical induction P(n) is true for all natural numbers n.

Q6. 3²ⁿ – 1 is divisible by 8, for all natural numbers
Sol: Let P(n): 3²ⁿ – 1 is divisible by 8, for all natural numbers n.
Now, P(l): 3² – 1 = 8, which is divisible by 8.
Hence, P(l) is true.
Let us assume that, P(n) is true for some natural number n = k.
P(k): 3^2k – 1 is divisible by 8
or               3^2k -1 = 8m, m ∈ N  (i)
Now, we have to prove that P(k + 1) is true.
P(k+ 1): 3^2(k+1)– l
= 3^2k • 3² — 1
= 9(8m + 1) – 1     (using (i))
= 72m + 9 – 1
= 72m + 8
= 8(9m +1), which is divisible by 8 Thus P(k + 1) is true whenever P(k) is true.
So, by the principle of mathematical induction P(n) is true for all natural numbers n.

Q7. For any natural number n, 7ⁿ – 2ⁿ is divisible by 5.
Sol: Let P(n): 7ⁿ – 2ⁿ is divisible by 5, for any natural number n.
Now, P(l) = 7¹-2¹ = 5, which is divisible by 5.
Hence, P(l) is true.
Let us assume that, P(n) is true for some natural number n = k.

.’.  P(k) = 7^k -2^k is divisible by 5
or  7^k – 2^k = 5m, m∈ N                                                                           (i)
Now, we have to prove that P(k + 1) is true.
P(k+ 1): 7^k+1 -2^k+1
= 7^k-7-2^k-2
= (5 + 2)7^k -2^k-2
= 5.7^k + 2.7^k-2-2^k
= 5.7^k + 2(7^k – 2^k)
= 5 • 7^k + 2(5 m)     (using (i))
= 5(7^k + 2m), which divisible by 5.
Thus, P(k + 1) is true whenever P(k) is true.
So, by the principle of mathematical induction P(n) is true for all natural numbers n.

Q8. For any natural number n, xⁿ -yⁿ is divisible by x -y, where x and y are any integers with x ≠y
Sol: Let P(n) : xⁿ – yⁿ is divisible by x – y, where x and y are any integers with x≠y.
Now, P(l): x¹ -y¹ = x-y, which is divisible by (x-y)
Hence, P(l) is true.
Let us assume that, P(n) is true for some natural number n = k.
P(k): x^k -y^k is divisible by (x – y)
or   x^k-y^k = m(x-y),m ∈ N …(i)
Now, we have to prove that P(k + 1) is true.
P(k+l):x^k+l-y^k+l
= x^k-x-x^k-y + x^k-y-y^ky
= x^k(x-y) +y(x^k-y^k)
= x^k(x – y) + ym(x – y)  (using (i))
= (x -y) [x^k+ym], which is divisible by (x-y)
Hence, P(k + 1) is true whenever P(k) is true.
So, by the principle of mathematical induction P(n) is true for any natural number n.

Q9. n³ -n is divisible by 6, for each natural number n≥
Sol: Let P(n): n³ – n is divisible by 6, for each natural number n> 2.
Now, P(2): (2)³ -2 = 6, which is divisible by 6.
Hence, P(2) is true.
Let us assume that, P(n) is true for some natural number n = k.
P(k): k³ – k is divisible by 6
or    k³ -k= 6m, m∈ N       (i)
Now, we have to prove that P(k + 1) is true.
P(k+ 1): (k+ l)³-(k+ 1)
= k³+ 1 +3k(k+ l)-(k+ 1)
= k³+ 1 +3k² + 3k-k- 1 = (k³-k) + 3k(k+ 1)
= 6m + 3 k(k +1)  (using (i))
Above is divisible by 6.   (∴ k(k + 1) is even)
Hence, P(k + 1) is true whenever P(k) is true.
So, by the principle of mathematical induction P(n) is true for any natural number n,n≥ 2.

Q10. n(n² + 5) is divisible by 6, for each natural number
Sol: Let P(n): n(n² + 5) is divisible by 6, for each natural number.
Now P(l): 1 (l² + 5) = 6, which is divisible by 6.
Hence, P(l) is true.
Let us assume that P(n) is true for some natural number n = k.
P(k): k( k² + 5) is divisible by 6.
or K (k²+ 5) = 6m, m∈ N         (i)
Now, we have to prove that P(k + 1) is true.
P(K+l):(K+l)[(K+l)² + 5]
= (K + l)[K² + 2K+6]
= K³ + 3 K² + 8K + 6
= (K² + 5K) + 3 K² + 3K + 6 =K(K² + 5) + 3(K² + K + 2)
= (6m) + 3(K² + K + 2)        (using (i))
Now, K² + K + 2 is always even if A is odd or even.
So, 3(K² + K + 2) is divisible by 6 and hence, (6m) + 3(K² + K + 2) is divisible by 6.
Hence, P(k + 1) is true whenever P(k) is true.
So, by the principle of mathematical induction P(n) is true for any natural number n.

Q11. n² < 2ⁿ, for all natural numbers n ≥
Sol: Let P(n): n² < 2ⁿ for all natural numbers n≥ 5.
Now P(5): 5² < 2⁵ or 25 < 32, which is true.
Hence, P(5) is true.
Let us assume that P(n) is true for some natural number n = k.
∴ P(k): k² < 2^k  (i)
Now, to prove that P(k + 1) is true, we have to show that P(k+ 1): (k+ l)² <2^k+1
Using (i), we get
(k + l)² = k² + 2k + 1 < 2^k + 2k + 1         (ii)
Now let, 2^k + 2k + 1 < 2^k+1     (iii)
∴ 2^k + 2k + 1 < 2 • 2^k
2k + 1 < 2^k, which is true for all k > 5 Using (ii) and (iii), we get (k + l)² < 2^k+1 Hence, P(k + 1) is true whenever P(k) is true.
So, by the principle of mathematical induction P(n) is true for any natural number n,n≥ 5.

Q12. 2n<(n + 2)! for all natural numbers
Sol: Let P(n): 2n < (n + 2)! for all natural numbers n.
P( 1): 2 < (1 + 2)! or 2 < 3! or 2 < 6, which is true.
Hence,P(l) is true.
Let us assume that P(n) is true for some natural number n = k.
P(k) :2k<(k + 2)!  (i)
To prove that P(k + 1) is true, we have to show that
P(k + 1): 2(k+ 1) < (k + 1 + 2)!
or 2(k+ 1) < (k + 3)!
Using (i), we get
2(k + 1) = 2k + 2<(k+2) !  +2  (ii)
Now let, (k + 2)! + 2 < (k + 3)!  (iii)
=>  2 < (k+ 3)! – (k+2) !
=> 2 < (k + 2) ! [k+ 3-1]
=>2<(k+ 2) ! (k + 2), which is true for any natural number.
Using (ii) and (iii), we get 2(k + 1) < (k + 3)!
Hence, P(k + 1) is true whenever P(k) is true.
So, by the principle of mathematical induction P(n) is true for any natural number n.

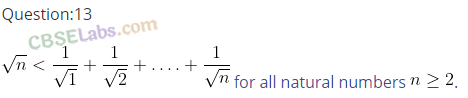
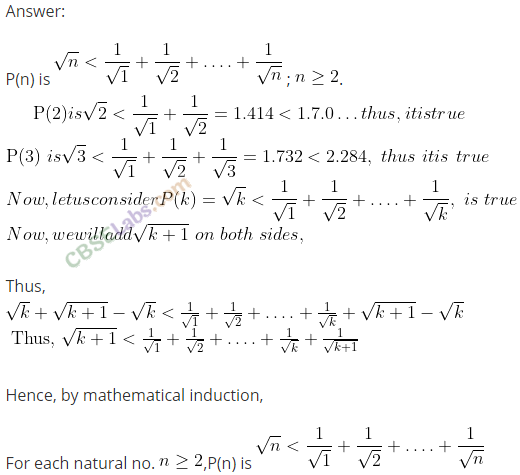
Q14. 2 + 4 + 6+… + 2n = n² + n, for all natural numbers
Sol: Let P(n) :2 + 4 + 6+ …+2 n = n² + n
P(l): 2 = l² + 1 = 2, which is true
Hence, P(l) is true.
Let us assume that P(n) is true for some natural number n = k.
∴ P(k): 2 + 4 + 6 + .,.+2k = k² + k  (i)
Now, we have to prove that P(k + 1) is true.
P(k + l):2 + 4 + 6 + 8+ …+2k+ 2 (k +1)
= k² + k + 2(k+ 1)  [Using (i)]
= k² + k + 2k + 2
= k² + 2k+1+k+1
= (k + 1)² + k+ 1
Hence, P(k + 1) is true whenever P(k) is true.
So, by the principle of mathematical induction P(n) is true for any natural number n.

Q15. 1 + 2 + 2² + … + 2ⁿ = 2^{n +1} – 1 for all natural numbers
Sol: Let P(n): 1 + 2 + 2² + … + 2ⁿ = 2^{n +1} – 1, for all natural numbers n
P(1): 1 =2^{0 + 1} — 1 = 2 — 1 = 1, which is true.
Hence, ,P(1) is true.
Let us assume that P(n) is true for some natural number n = k.

P(k): l+2 + 2²+…+2^k = 2^k+1-l              (i)

Now, we have to prove that P(k + 1) is true.

P(k+1): 1+2 + 2²+ …+2^k + 2^k+1
= 2^{k +1} – 1 + 2^k+1  [Using (i)]
= 2.2^k+l– 1 = 1
₌ 2^(k+1)+1-1
Hence, P(k + 1) is true whenever P(k) is true.
So, by the principle of mathematical induction P(n) is true for any natural number n.

Q16. 1 + 5 + 9 + … + (4n – 3) = n(2n – 1), for all natural numbers
Sol: Let P(n): 1 + 5 + 9 + … + (4n – 3) = n(2n – 1), for all natural numbers n.
P(1): 1 = 1(2 x 1 – 1) = 1, which is true.
Hence, P(l) is true.
Let us assume that P(n) is true for some natural number n = k.
∴ P(k):l+5 + 9 +…+(4k-3) = k(2k-1)  (i)
Now, we have to prove that P(k + 1) is true.
P(k+ 1): 1 + 5 + 9 + … +  (4k- 3) + [4(k+ 1) – 3]
= 2k² -k+4k+ 4-3
= 2k² + 3k + 1
= (k+ 1)( 2k + 1)

= (k+l)[2(k+l)-l]

Hence, P(k + 1) is true whenever P(k) is true.

So, by the principle of mathematical induction P(n) is true for any natural number n.

Long Answer Type Questions
Q17. A sequence a_x, a₂, a₃, … is defined by letting a₁=3 and a_k = 7a_k–₁ for all natural numbers k≥ Show that a_n = 3 • 7 ^n-1 for all natural numbers.
Sol: We have a sequence a_x, a₂, a₃… defined by letting a, = 3 and a_k = 7a_k–₁, for all natural numbers k≥2.

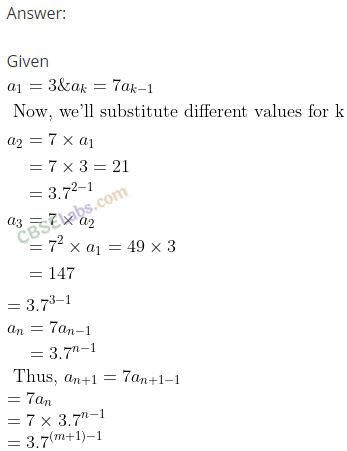
Q18. A sequence b₀, b₁, b₂, … is defined by letting b₀ = 5 and b_k = 4 + b_k–₁, for all natural numbers Show that b_n = 5 + 4n, for all natural number n using mathematical induction.
Sol. We have a sequence b₀, b₁, b₂,… defined by letting b₀ = 5 and b_k = 4 + b_k–₁,, for all natural numbers k.

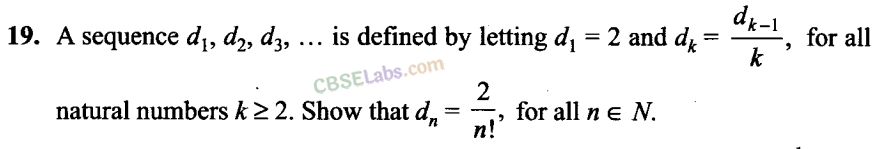
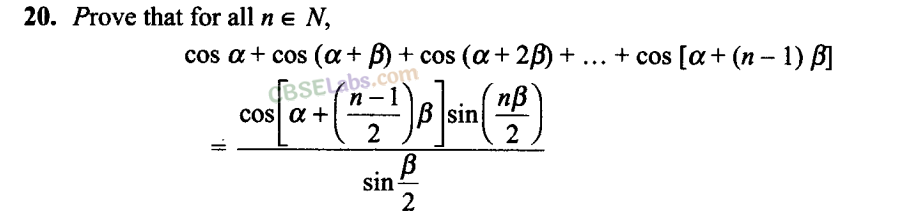
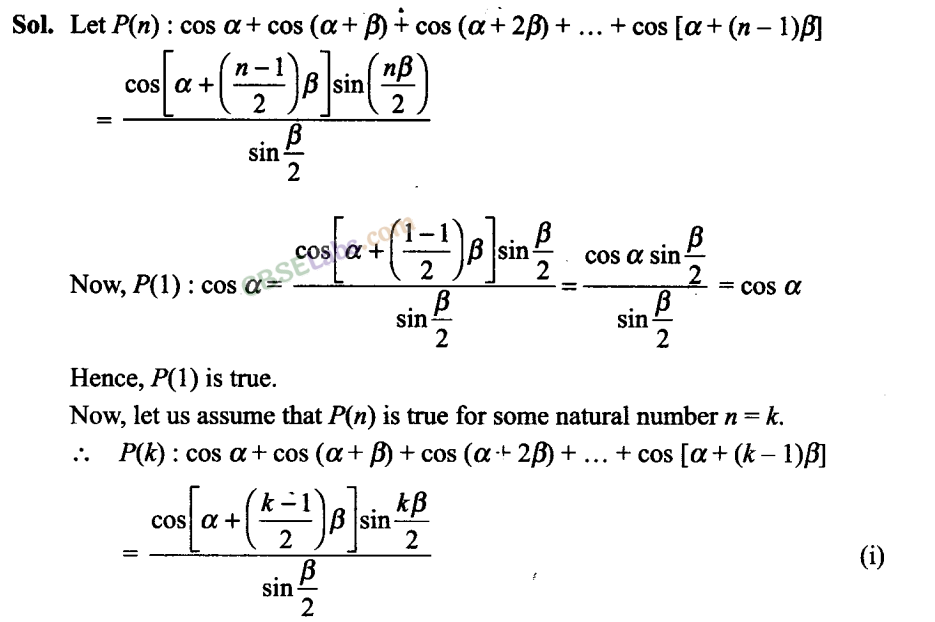
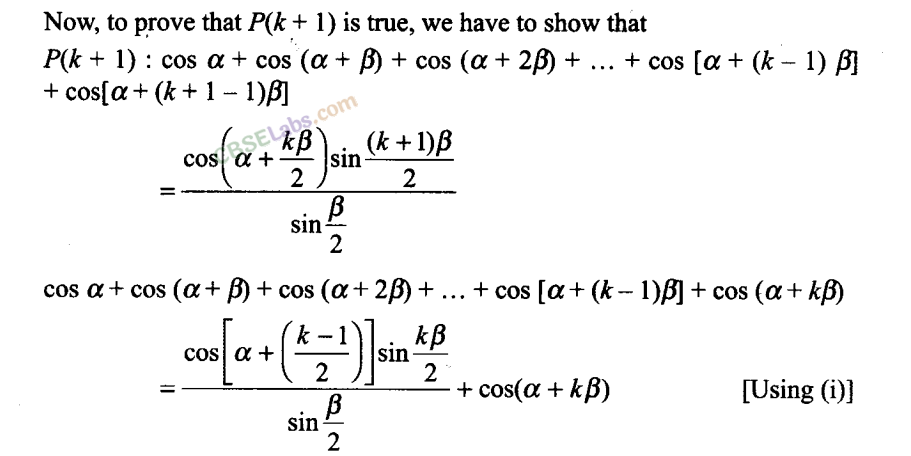
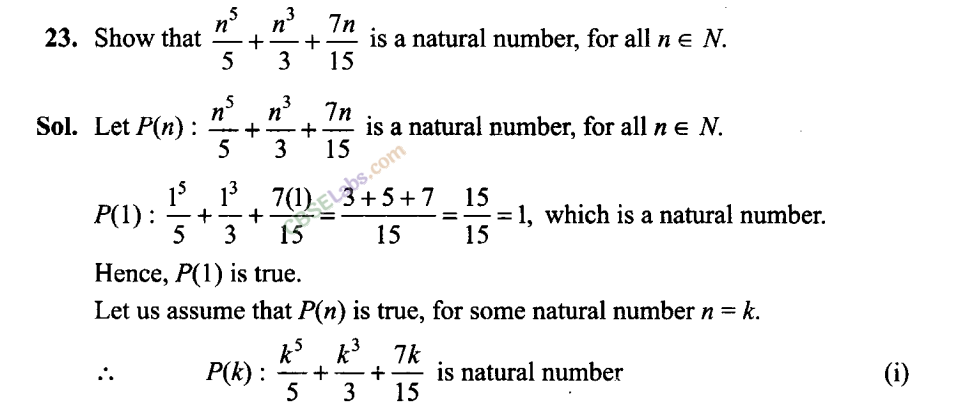
So, by the principle of mathematical induction P(n) is true for any natural number rt,n> 1.

Q25. Prove that number of subsets of a set containing n distinct elements is 2″, for all n ∈
Sol: Let P(n): Number of subset of a set containing n distinct elements is 2″, for all ne N.
For n = 1, consider set A = {1}. So, set of subsets is {{1}, ∅}, which contains 2¹ elements.
So, P(1) is true.
Let us assume that P(n) is true, for some natural number n = k.
P(k): Number of subsets of a set containing k distinct elements is 2^k To prove that P(k + 1) is true,
we have to show that P(k + 1): Number of subsets of a set containing (k + 1) distinct elements is 2^k+1
We know that, with the addition of one element in the set, the number of subsets become double.
Number of subsets of a set containing (k+ 1) distinct elements = 2×2^k = 2^k+1
So, P(k + 1) is true. Hence, P(n) is true.

NCERT Exemplar ProblemsMathsPhysicsChemistryBiology

We hope the NCERT Exemplar Class 11 Maths Chapter 4 Principle of Mathematical Induction help you. If you have any query regarding NCERT Exemplar Class 11 Maths Chapter 4 Principle of Mathematical Induction, drop a comment below and we will get back to you at the earliest.