NCERT Exemplar Class 11 Maths Chapter 11 Conic Sections of NCERT Exemplar Class 11 Maths. Here we have given NCERT Exemplar Class 11 Maths Chapter 11 Conic Sections.
NCERT Exemplar Class 11 Maths Chapter 11 Conic Sections
Short Answer Type Questions
Q1. Find the equation of the circle which touches the both axes in first quadrant and whose radius is a.
Sol: Given that the circle of radius ‘a’ touches both axis. So, its centre is (a, a).

Q2. Show that the point (x, y) given by \(x=\frac { 2at }{ 1+{ t }^{ 2 } } \) and \(y=\frac { 1-{ t }^{ 2 } }{ 1+{ t }^{ 2 } } \) lies on a circle .
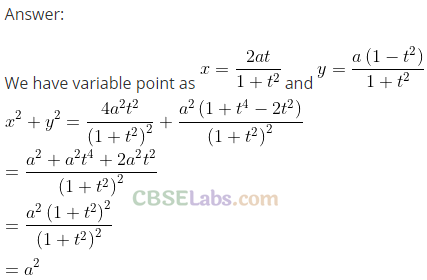
Q3. If a circle passes through the point (0, 0) (a, 0), (0, b) then find the coordinates of its centre.
Sol: We have circle through the point A(0, 0), B(a, 0) and C(0, b).
Clearly triangle is right angled at vertex A.
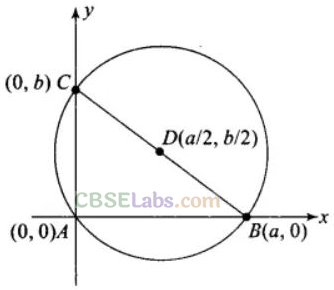
So, centre of the circle is the mid point of hypotenuse BC which is (a/2, b/2)
Q4. Find the equation of the circle which touches x-axis and whose centre is (1,2).
Sol: Given that, circle with centre (1,2) touches x-axis.
Radius of the circle is, r = 2
So, the equation of the required circle is:
(x – l)2 + (y – 2)2 = 22
=>x2-2x + 1 + y2-4y + 4 = 4
=> x2 + y2 – 2x-4y + 1 = 0
Q5. If the lines 3x – 4y + 4 = 0 and 6x – 8y – 7 = 0 are tangents to a circle, then find the radius of the circle.
Sol: Given lines are 6x – 8y + 8 = 0 and 6x – 8y – 7 = 0.
These parallel lines are tangent to a circle.

Q6. Find the equation of a circle which touches both the axes and the line 3x – 4y + 8 = 0 and lies in the third quadrant.

Q7. If one end of a diameter of the circle x2 + y2 -4x -6y + 11 = 0 is (3,4), then find the coordinate of the other end of the diameter.
Sol: Given equation of the circle is:

Q8. Find the equation of the circle having (1, -2) as its centre and passing through 3x +y= 14, 2x + 5y = 18.
Sol: Given lines are 3x + y = 14 and 2x + 5y= 18.

Q9. If the line y= √3 x + k touches the circle x2 + y2 = 16, then find the value of
Sol: Given line is y = √3 x + k and the circle is x2 + y2 = 16.

Q10. Find the equation of a circle concentric with the circle x2 +y2 – 6x + 12y + 15 = 0 and has double of its area.
Sol: Given equation of the circle is:

Q11. If the latus rectum of an ellipse is equal to half of minor axis, then find its eccentricity.
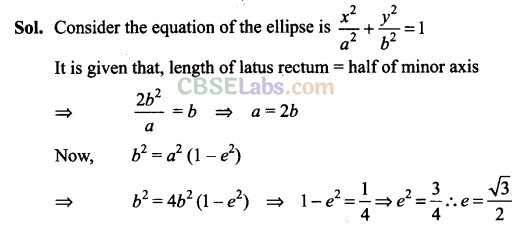
Q12. Given the ellipse with equation 9X2 + 25y2 = 225, find the eccentricity and foci.

Q13. If the eccentricity of an ellipse is 5/8 and the distance between its foci is 10, then find latus rectum of the ellipse.

Q14. Find the equation of ellipse whose eccentricity is 2/3, latus rectum is 5 and thecentre is (0, 0).

Q15. Find the distance between the directrices of the ellipse \(\frac { { x }^{ 2 } }{ 36 } +\quad \frac { { y }^{ 2 } }{ 20 } \quad =\quad 1 \)

Q16. Find the coordinates of a point on the parabola y2 = 8x whose focal distance is 4.
Sol: Given parabola is y2 = 8x

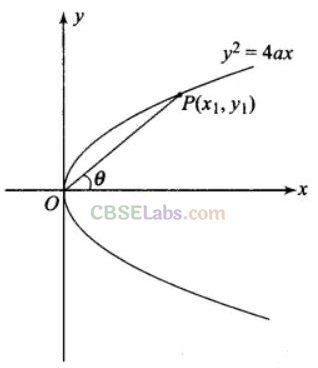
Q17. Find the length of the line-segment joining the vertex of the parabola y2 = 4ax and a point on the parabola where the line-segment makes an angle 6 to the x-axis.
Sol: Given equation of the parabola isy2 = 4ax.
Let the point on the parabola be P(x1,,y1).

Q18. If the points (0, 4) and (0, 2) are respectively the vertex and focus of a parabola, then find the equation of the parabola.

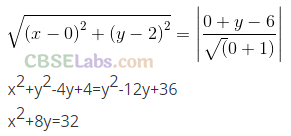
Q19. If the line y = mx + 1 is tangent to the parabola y2 = 4x then find the value of m.
Sol: Given that, liney = mx + 1 is tangent to the parabola y2 = 4x.

Q20. If the distance between the foci of a hyperbola is 16 and its eccentricity is √2, then obtain the equation of the hyperbola.

Q21. Find the eccentricity of the hyperbola 9y2 – 4x2 =36
Sol: We have the hyperbola:9y2 – 4x2 = 36
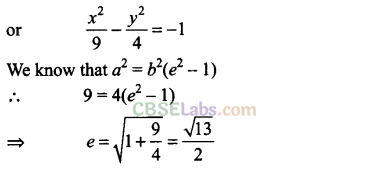
Q22. Find the equation of the hyperbola with eccentricity 3/2 and foci at (±2, 0).

Long Answer Type Questions
Q23. If the lines 2x – 3y = 5 and 3x-4y = 7 are the diameters of a circle of area 154 square units, then obtain the equation of the circle.
Sol: Given that lines 2x – 3y – 5 = 0 and 3x – 4y -1 = 0 are diameters of the circle. Solving these lines we get point of intersection as (1, -1), which is centre of the circle.
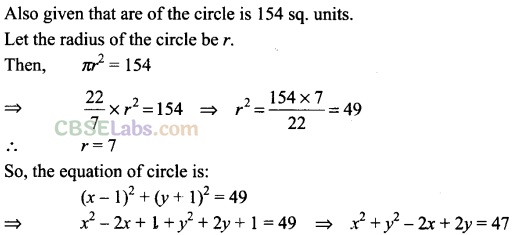
Q24. Find the equation of the circle which passes through the points (2, 3) and (4, 5) and the centre lies on the straight line y – 4x + 3 = 0.

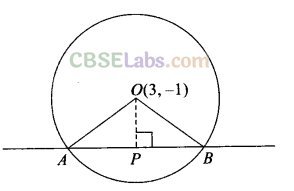
Q25. Find the equation of a circle whose centre is (3, -1) and which cuts off a chord of length 6 units on the line 2x — 5y+ 18 = 0.
Sol: Given centre of the circle 0(3, -1)
Chord of the circle is AB.

Q26. Find the equation of a circle of radius 5 which is touching another circle x2 + y2 – 2x – 4y – 20 = 0 at (5, 5).

Q27. Find the equation of a circle passing through the point (7, 3) having radius 3 units and whose centre lies on the line y = x -1.
Sol: Given that circle passes through the point A(7, 3) and its radius is 3.

Q28. Find the equation of each of the following parabolas.
(i) Directrix, x = 0, focus at (6, 0)
(ii) Vertex at (0,4), focus at (0, 2)
(iii) Focus at (-1, -2), directrix x – 2y + 3 = 0
Sol: We know that the distance of any point on the parabola from its focus and its directrix is same.
(i) Given that, directrix, x = 0 and focus = (6, 0)
So, for any point P(x, y) on the parabola
Distance of P from directrix = Distance of P from focus => x2 = (x — 6)2 + y2
=> y2– 12x + 36 = 0
(ii) Given that, vertex = (0,4) and focus = (0, 2)
Now distance between the vertex and directrix is same as the distance between the vertex and focus.
Directrix is y – 6 = 0
For any point of P(x, y) on the parabola
Distance of P from directrix = Distance of P from focus

Q29. Find the equation of the set of all points the sum of whose distances from the points (3, 0) and (9, 0) is 12.
Sol: Let the coordinates of the variable point be (x, y).
Then according to the question,

Q30. Find the equation of the set of all points whose distance from (0,4) are 2/3 of their distance from the line y = 9.
Sol: Let the point be P(x, y).
According to the question
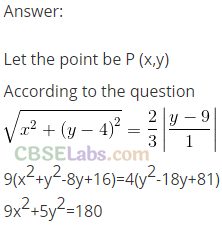
Q31. Show that the set of all points such that the difference of their distances from (4, 0)and (-4, 0) is always equal to 2 represent a hyperbola.



True/False Type Questions
Q33. The line x + 3y = 0 is a diameter of the circle x2 + y2 + 6x + 2y = 0.
Sol: False
Given equation of the circle is x2 + y2 + 6x + 2y = 0
Centre = (-3, -1)
Clearly, it does not lie on the line x + 3y = 0 as -3 + 3(-l) = -6.
So, this line is not diameter of the circle.
Q34. The shortest distance from the point (2, -7) to the circle x +y2 – 1 4jc – lOy- 151 = 0 is equal to 5.
Sol: False

Q35. If the line lx + my = 1 is a tangent to the circle x2 + y2 = a2, then the point (1, m) lies on a circle.

Q36. The point (1,2) lies inside the circle x2 + y2 – 2x + 6y + 1 = 0.
Sol: False

Q37. The line lx+ my + n = 0 will touch the parabola^2 = 4 ax if In = am2.
Sol: True




Fill in the Blanks Type Questions
Q41. The equation of the circle having centre at (3, -4) and touching the line 5x + 12y- 12 = 0 is ______.
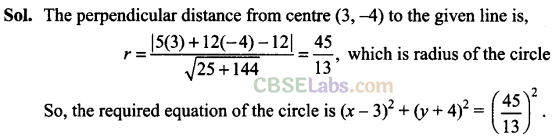
Q42. The equation of the circle circumscribing the triangle whose sides are the lines y = x + 2, 3y = 4x, 2y = 3x is _______.
Given equation of line are:

Q43. An ellipse is described by using an endless string which is passed over two pins. If the axes are 6 cm and 4 cm, the length of the string and distance between the pins are _____ .

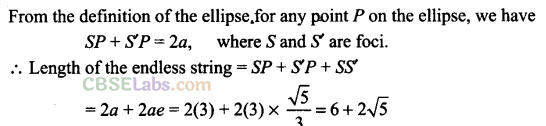
Q44. The equation of the ellipse having foci (0,1), (0, -1) and minor axis of length 1 is ___ .

Q45. The equation of the parabola having focus at (-1, -2) and the directrix x – 2y + 3 = 0 is______ .
Sol: Given that, focus at S(-l, -2) and directrix is x – 2y + 3 = 0
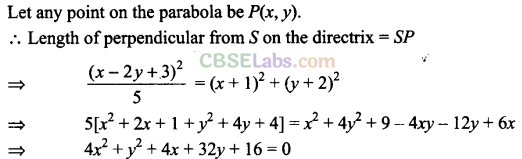
Q46. The equation of the hyperbola with vertices at (0, ±6) and eccentricity 5/3 ________ and its foci are _____ .
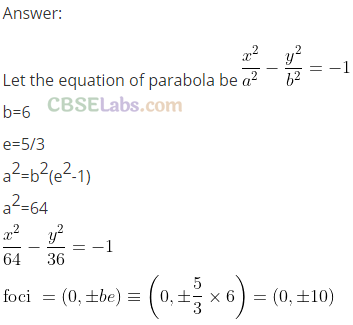
Objective Type Questions
Q47. The area of the circle centred at (1,2) and passing through (4, 6) is
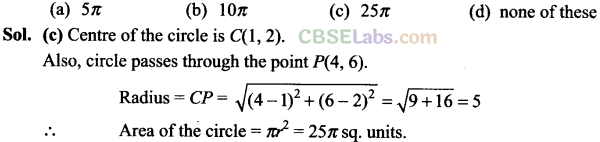
Q48. Equation of a circle which passes through (3, 6) and touches the axes is
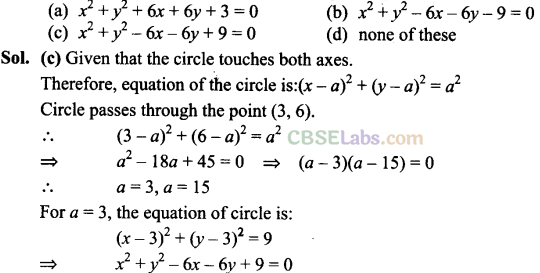
Q49. Equation of the circle with centre on the j-axis and passing through the origin and the point (2, 3) is

Q50. The equation of a circle with origin as centre and passing through the vertices of an equilateral triangle whose median is of length 3a is
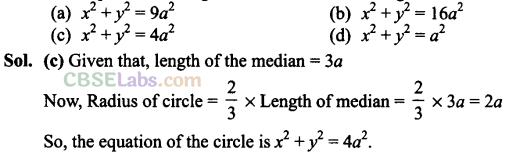
Q51. If the focus of a parabola is (0, -3) and its directrix is y = 3, then its equation is

Q52. If the parabola y2 = 4ax passes through the point (3, 2), then the length of its latus rectum is

Q53. If the vertex of the parabola is the point (-3, 0) and the directrix is the line x + 5 = 0, then its equation is
(a) y2 = 8(x + 3)
(b) x2 = 8(y + 3)
(c) y2 = -8(x + 3)
(d) y2 = 8(x + 5)

Q54. The equation of the ellipse whose focus is (1, -1), the directrix the line x-y-3 = 0 and eccentricity 1/2 is

Q55. The length of the latus rectum of the ellipse 3x2 +y2 = 12 is
(a) 4
(b) 3
(c) 8
(d) 4/√3


NCERT Exemplar Class 11 Maths Solutions
- Chapter 1 Sets
- Chapter 2 Relations and Functions
- Chapter 3 Trigonometric Functions
- Chapter 4 Principle of Mathematical Induction
- Chapter 5 Complex Numbers and Quadratic Equations
- Chapter 6 Linear Inequalities
- Chapter 7 Permutations and Combinations
- Chapter 8 Binomial Theorem
- Chapter 9 Sequence and Series
- Chapter 10 Straight Lines
- Chapter 11 Conic Sections
- Chapter 12 Introduction to Three-Dimensional Geometry
- Chapter 13 Limits and Derivatives
- Chapter 14 Mathematical Reasoning
- Chapter 15 Statistics
- Chapter 16 Probability
NCERT Exemplar ProblemsMathsPhysicsChemistryBiology
We hope the NCERT Exemplar Class 11 Maths Chapter 11 Conic Sections help you. If you have any query regarding NCERT Exemplar Class 11 Maths Chapter 11 Conic Sections, drop a comment below and we will get back to you at the earliest.