Get Free NCERT Solutions for Class 11 Maths Chapter 12 Introduction to three Dimensional Geometry Ex 12.2 PDF in Hindi and English Medium. Introduction to three Dimensional Geometry Class 11 Maths NCERT Solutions are extremely helpful while doing your homework. Introduction to three Dimensional Geometry Ex 12.2 Class 11 Maths NCERT Solutions were prepared by Experienced LearnCBSE.in Teachers. Detailed answers of all the questions in Chapter 12 Class 11 Introduction to three Dimensional Geometry Ex 12.2 provided in NCERT Textbook.
- Introduction to Three Dimensional Geometry Class 11 Ex 12.1
- Introduction to Three Dimensional Geometry Ex 12.2
- Introduction to Three Dimensional Geometry Ex 12.3
- Introduction to Three Dimensional Geometry Miscellaneous Exercise
- त्रिविमीय ज्यामिति का परिचय प्रश्नावली 12.1 का हल हिंदी में
- त्रिविमीय ज्यामिति का परिचय प्रश्नावली 12.2 का हल हिंदी में
- त्रिविमीय ज्यामिति का परिचय प्रश्नावली 12.3 का हल हिंदी में
- त्रिविमीय ज्यामिति का परिचय विविध प्रश्नावली का हल हिंदी में
- Introduction to Three Dimensional Geometry Class 11 Notes
- NCERT Exemplar Class 11 Maths Introduction to Three Dimensional Geometry
- Three Dimensional Geometry JEE Main Mathematics Previous Year Questions
Free download NCERT Solutions for Class 11 Maths Chapter 12 Introduction to three Dimensional Geometry Ex 12.2 PDF in Hindi Medium as well as in English Medium for CBSE, Uttarakhand, Bihar, MP Board, Gujarat Board, BIE, Intermediate and UP Board students, who are using NCERT Books based on updated CBSE Syllabus for the session 2019-20.
NCERT Solutions for Class 11 Maths Chapter 12 Introduction to three Dimensional Geometry Ex 12.2

Question 1.
Find the distance between the following pairs of points:
(i) (2, 3, 5) and (4, 3, 1)
(ii) (-3, 7, 2) and (2, 4, -1)
(iii) (-1, 3, -4) and (1, -3, 4)
(iv) (2, -1, 3) and (-2, 1, 3)
Solution:
(i) The distance PQ between the points P(2, 3, 5) and Q(4, 3, 1) is
\(PQ=\sqrt { \left( 4-2 \right) ^{ 2 }+\left( 3-3 \right) ^{ 2 }\left( 1-5 \right) ^{ 2 } } \)
= \(\sqrt { 4+0+16= } \sqrt { 20 } =2\sqrt { 5 } units.\)
(ii) The distance PQ between the points P(-3, 7, 2) and Q(2, 4, -1) is
\(PQ=\sqrt { \left[ 2-\left( -3 \right) \right] ^{ 2 }+\left( 4-7 \right) ^{ 2 }\left( -1-2 \right) ^{ 2 } } \)
\(=\sqrt { \left( 2+3 \right) ^{ 2 }+\left( 4-7 \right) ^{ 2 }+\left( -1-2 \right) ^{ 2 } } \)
\(=\sqrt { 25+9+9 } =\sqrt { 43 } units\)
(iii) The distance PQ between the points P(-1, 3, -4) and Q(1, -3, 4) is
\(PQ=\sqrt { \left[ 1-\left( -1 \right) \right] ^{ 2 }+\left( -3-3 \right) ^{ 2 }\left[ 4-\left( -4 \right) \right] ^{ 2 } } \)
\(=\sqrt { 4+36+64 } =\sqrt { 104 } =2\sqrt { 26 } units\)
(iv) The distance PQ between the points P(2, -1, 3) and Q(-2, 1, 3) is
\(PQ=\sqrt { \left( -2-2 \right) ^{ 2 }+\left[ 1-\left( -1 \right) \right] ^{ 2 }+\left( 3-3 \right) ^{ 2 } } \)
\(=\sqrt { 16+4+0 } =\sqrt { 20 } =2\sqrt { 5 } units\)
Question 2.
Show that the points (-2, 3, 5), (1, 2, 3) and (7, 0, -1) are collinear.
Solution:
Let A(-2, 3, 5), B(1, 2, 3) and C(7, 0, -1) be three given points.
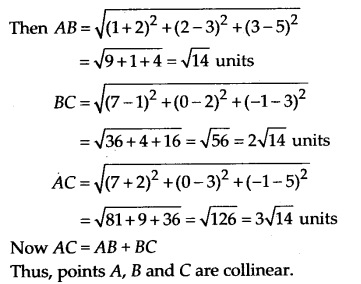
Question 3.
Verify the following:
(i) (0, 7, -10), (1, 6, -6) and (4, 9, -6) are the vertices of an isosceles triangle.
(ii) (0, 7, 10), (-1, 6, 6) and (-4, 9, 6) are the vertices of a right angled triangle.
(iii) (-1, 2, 1), (1, -2, 5), (4, -7,8) and (2, -3,4) are the vertices of a parallelogram.
Solution:
(i) Let A(0, 7, -10), B(l, 6, -6) and C(4, 9, -6) be three vertices of triangle ABC. Then
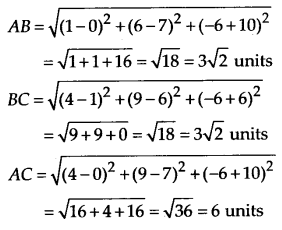
Now, AB = BC
Thus, ABC is an isosceles triangle.
(ii) Let A(0, 7,10), B(-l, 6, 6) and C(-A, 9, 6) be three vertices of triangle ABC. Then
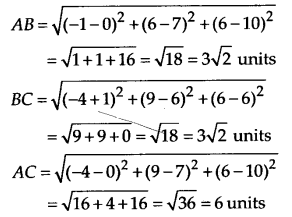
Now, AC2 = AB2 + BC2
Thus, ABC is a right angled triangle.
(iii) Let A(-1, 2, 1), B(1, -2, 5) and C(4, -7, 8) and D(2, -3,4) be four vertices of quadrilateral ABCD. Then
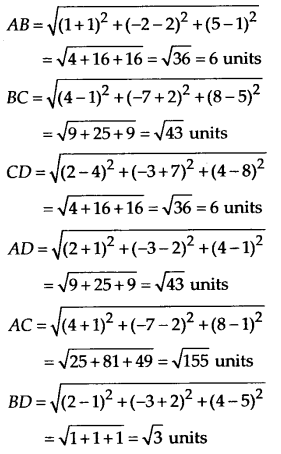
Now AB = CD, BC = AD and AC ≠ BD
Thus A, B, C and D are vertices of a parallelogram ABCD.
Question 4.
Find the equation of the set of points which are equidistant from the points (1, 2, 3) and (3, 2, -1).
Solution:
Let A(x, y, z) be any point which is equidistant from points B(1, 2, 3) and C(3, 2, -1).
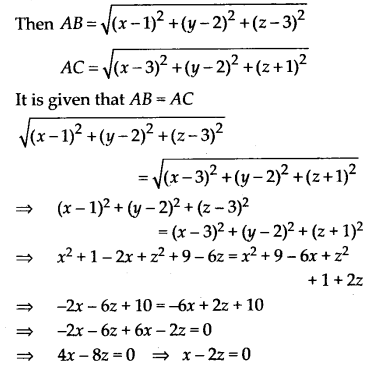
Question 5.
Find the equation of the set of points P, the sum of whose distances from A(4, 0, 0) and B(-4,0,0) is equal to 10.
Solution:
Let P(x, y, z) be any point.
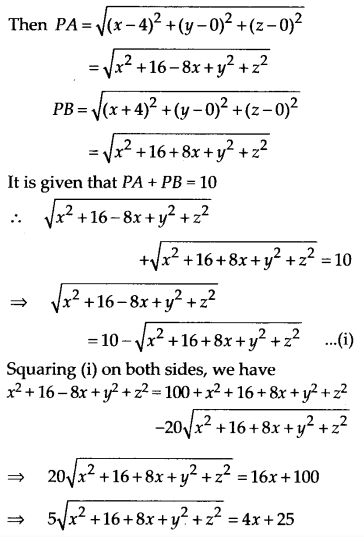
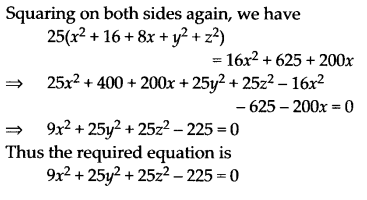
NCERT Solutions for Class 11 Maths Chapter 12 Introduction to Three Dimensional Geometry (त्रिविमीय ज्यामिति का परिचय) Hindi Medium Ex 12.2






NCERT Solutions for Class 11 Maths All Chapters
- Chapter 1 Sets
- Chapter 2 Relations and Functions
- Chapter 3 Trigonometric Functions
- Chapter 4 Principle of Mathematical Induction
- Chapter 5 Complex Numbers and Quadratic Equations
- Chapter 6 Linear Inequalities
- Chapter 7 Permutation and Combinations
- Chapter 8 Binomial Theorem
- Chapter 9 Sequences and Series
- Chapter 10 Straight Lines
- Chapter 11 Conic Sections
- Chapter 12 Introduction to Three Dimensional Geometry
- Chapter 13 Limits and Derivatives
- Chapter 14 Mathematical Reasoning
- Chapter 15 Statistics
- Chapter 16 Probability