Mathematical Reasoning Class 11 Maths NCERT Solutions are extremely helpful while doing your homework. NCERT Solutions for Class 11 Maths Chapter 14 Mathematical Reasoning All Exercises were prepared by Experienced LearnCBSE.in Teachers.
Free download NCERT Solutions for Class 11 Maths Chapter 14 Mathematical Reasoning Ex 14.1, Ex 14.2, Ex 14.3, Ex 14.4, Ex 14.5 and Miscellaneous Exercise PDF in Hindi Medium as well as in English Medium for CBSE, Uttarakhand, Bihar, MP Board, Gujarat Board, BIE, Intermediate and UP Board students, who are using NCERT Books based on updated CBSE Syllabus for the session 2019-20.
- Mathematical Reasoning Class 11 Ex 14.1
- Mathematical Reasoning Class 11 Ex 14.2
- Mathematical Reasoning Class 11 Ex 14.3
- Mathematical Reasoning Class 11 Ex 14.4
- Mathematical Reasoning Class 11 Ex 14.5
- Mathematical Reasoning Class 11 Miscellaneous Exercise
- गणितीय विवेचन प्रश्नावली 14.1 का हल हिंदी में
- गणितीय विवेचन प्रश्नावली 14.2 का हल हिंदी में
- गणितीय विवेचन प्रश्नावली 14.3 का हल हिंदी में
- गणितीय विवेचन प्रश्नावली 14.4 का हल हिंदी में
- गणितीय विवेचन प्रश्नावली 14.5 का हल हिंदी में
- गणितीय विवेचन विविध प्रश्नावली का हल हिंदी में
NCERT Solutions for Class 11 Maths Chapter 14 Mathematical Reasoning

Topics and Sub Topics in Class 11 Maths Chapter 14 Mathematical Reasoning:
| Section Name | Topic Name |
| 14 | Mathematical Reasoning |
| 14.1 | Introduction |
| 14.2 | Statements |
| 14.3 | New Statements from Old |
| 14.4 | Special Words/Phrases |
| 14.5 | Implications |
| 14 .6 | Validating Statements |
NCERT Solutions for Class 11 Maths Chapter 14 Exercise.14.1
Ex 14.1 Class 11 Maths Question-1

Ans.

Ex 14.1 Class 11 Maths Question-2
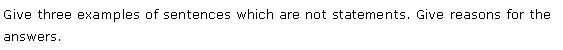
Ans.

NCERT Solutions for Class 11 Maths Chapter 14 Mathematical Reasoning (गणितीय विवेचन) Hindi Medium Ex 14.1


More Resources for CBSE Class 11
- NCERT Solutions
- NCERT Solutions Class 11 Maths
- NCERT Solutions Class 11 Physics
- NCERT Solutions Class 11 Chemistry
- NCERT Solutions Class 11 Biology
- NCERT Solutions Class 11 Hindi
- NCERT Solutions Class 11 English
- NCERT Solutions Class 11 Business Studies
- NCERT Solutions Class 11 Accountancy
- NCERT Solutions Class 11 Psychology
- NCERT Solutions Class 11 Entrepreneurship
- NCERT Solutions Class 11 Indian Economic Development
- NCERT Solutions Class 11 Computer Science
NCERT Solutions for Class 11 Maths Chapter 14 Exercise.14.2
Ex 14.2 Class 11 Maths Question-1

Ans.

Ex 14.2 Class 11 Maths Question-2

Ans.

Ex 14.2 Class 11 Maths Question-3

Ans.

NCERT Solutions for Class 11 Maths Chapter 14 Exercise.14.3
Ex 14.3 Class 11 Maths Question-1

Ans.

Ex 14.3 Class 11 Maths Question-2
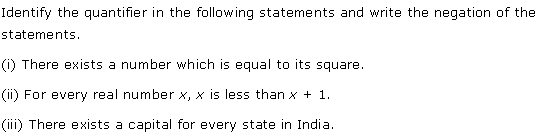
Ans.

Ex 14.3 Class 11 Maths Question-3

Ans.
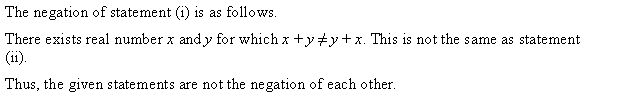
Ex 14.3 Class 11 Maths Question-4

Ans.

NCERT Solutions for Class 11 Maths Chapter 14 Exercise.14.4
Ex 14.4 Class 11 Maths Question-1

Ans.
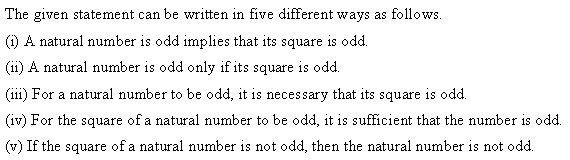
Ex 14.4 Class 11 Maths Question-2

Ans.

Ex 14.4 Class 11 Maths Question-3

Ans.

Ex 14.4 Class 11 Maths Question-4

Ans.

NCERT Solutions for Class 11 Maths Chapter 14 Exercise.14.5
Ex 14.5 Class 11 Maths Question-1
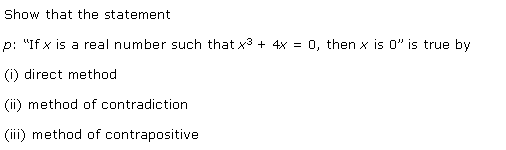
Ans.


Ex 14.5 Class 11 Maths Question-2
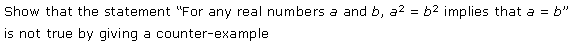
Ans.

Ex 14.5 Class 11 Maths Question-3
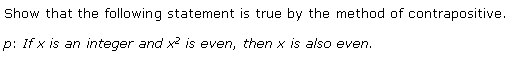
Ans.

Ex 14.5 Class 11 Maths Question-4
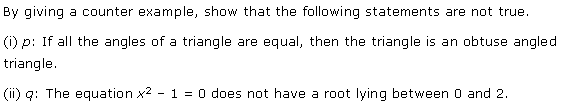
Ans.

Ex 14.5 Class 11 Maths Question-5

Ans.

Class 11 Maths NCERT Solutions – Mathematical Reasoning Miscellaneous Questions
Miscellaneous Exercise Class 11 Maths Question-1

Ans.

Miscellaneous Exercise Class 11 Maths Question-2

Ans.

Miscellaneous Exercise Class 11 Maths Question-3

Ans.

Miscellaneous Exercise Class 11 Maths Question-4

Ans.

Miscellaneous Exercise Class 11 Maths Question-5

Ans.

Miscellaneous Exercise Class 11 Maths Question-6
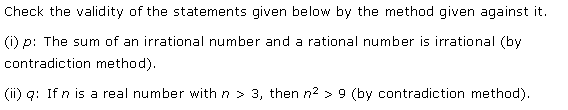
Ans.

Miscellaneous Exercise Class 11 Maths Question-7
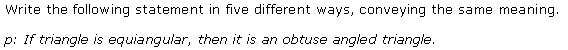
Ans.

Q.1: State whether the following sentences are statements or not, and justify your answers.
(a) A month has 35 days.
(b) Mathematics is very tough
(c) Addition of two numbers such as 5 & 7 is larger than 10.
(d) The resultant of a square of a number is always an even number.
(e) The arms of a quadrilateral are having equal length.
(f) Answer the following questions.
(g) The multiplication result of two numbers such as 8 and (-1) is 8
(h) The interior angles summed up together results in 1800 in a triangle.
(i) Yesterday was a cloudy day.
(j) The numbers which are real are always complex numbers.
Q.2: Give 3 examples of each sentence which are not statements. Give justified reasons for the answers.
Exercise 14.2
Q.1: Write the opposite of the below mentioned statements:
(a). New Delhi is the capital of India.
(b). √3+1 is a complex number.
(c). All quadrilaterals are not squares.
(d). 9 is lesser than 7
(e). The square of every natural number is a even number
Q.2: State whether the following statements are opposite to each other or not.
(a). The number 2 is not an even number
The number 2 is not an odd number.
(b). The number 2 is an even number.
The number 2 is an odd number.
Q.3: Find out the component sentences from the below-mentioned compound sentences, and determine whether they are true/ false.
(a). Number 5 is odd or it is a prime number.
(b). All integers are positive and negative.
(c). 1000 is divisible by 9 or 10
Exercise 14.3
Q.1:
(i). Every real number is not complex number and every rational number is a real number.
(ii). Square of any integer is negative or positive.
(iii). The sand easily heats up due to the sun but does not cool down easily at night
(iv). The roots for the equation x + 10 = 3x2 are x = 3 and x = 2
Q.2: Write negation for the statements after identifying the quantifier for the statements
(i). There exits one number that is equal to the square of the number
(ii). For every number that is real ‘x’, x < x + 1
(iv). There exist one capital for each state of India.
Q.3: Check if the following statements are negation for each other. Justify your answer
(i). y + x = x + y is true for real numbers x and y
(ii). There exist real numbers x, y such that y + x = x + y
Q.4: State if the “Or” in the statements is inclusive or exclusive. Justify the answer
(i) Moon sets or sun rises
(ii) You must have ration card or passport for applying a driving license.
(iii) Integers are negative or positive
Exercise – 14.4
Q.1: Rewrite the statements with ‘if & then’ in 5 different ways but the sentence should convey the meaning as before.
A natural number is odd implies that its square is odd.
Q.2: Rewrite the following sentences as the converse/contrapositive of the followings:
(a). A quadrilateral is said to be parallelogram if the diagonals bisect each other.
(b). y is an odd number that is y is divisible by 3
(c). If 2 lines do not intersect in the same plane, then they are said to be parallel.
(d). If something is having a low temperature then it implies that is cold
(e). If you are not able to deduct the reason, then you will not be able to comprehend geometry.
Q.3: Rewrite the following sentences with “if- then”:
(a). You have visited Qutub Minar implies that you live in Delhi
(b). You will pass the exam if you study hard.
(c). In order to get A+ in the class test, you have to do all the problems of that chapter.
(d). Parallel lines do not intersect each other in the same plane
Q.4: Identify the contrapositive/converse from the following sentences:
(i) If you live in Agra, then you have visited Taj Mahal
(a) If you have not visited Taj Mahal then you do not live in Agra.
(b) If you have visited Taj Mahal then you live in Agra.
(ii) If the diagonals of the quadrilateral bisect each other then that quadrilateral is a parallelogram.
(a) A quadrilateral is not said to be a parallelogram if the diagonals of a quadrilateral do not bisect each other.
(b) A quadrilateral is said to be a parallelogram if the diagonals of a quadrilateral bisect each other.
Exercise 14.5
Q.1: Prove that p: “If a is real such that a3+ 4a = 0, then a is 0″ is true
(i). by direct method
(ii). by method of contradiction
(iii). by method of contra positive
Q.2: Prove the statement “For real numbers b and a, b2 = a2 implies that b = a” isn’t true. Give a counter example.
Q3: By using contrapositive method prove the following statement is true
p: if a is an integer and a2 is even, then a is even.
NCERT Solutions for Class 11 Maths All Chapters
- Chapter 1 Sets
- Chapter 2 Relations and Functions
- Chapter 3 Trigonometric Functions
- Chapter 4 Principle of Mathematical Induction
- Chapter 5 Complex Numbers and Quadratic Equations
- Chapter 6 Linear Inequalities
- Chapter 7 Permutation and Combinations
- Chapter 8 Binomial Theorem
- Chapter 9 Sequences and Series
- Chapter 10 Straight Lines
- Chapter 11 Conic Sections
- Chapter 12 Introduction to Three Dimensional Geometry
- Chapter 13 Limits and Derivatives
- Chapter 14 Mathematical Reasoning
- Chapter 15 Statistics
- Chapter 16 Probability