NCERT Solutions for Class 11 Maths Chapter 1 Sets Miscellaneous Exercise
Get Free NCERT Solutions for Class 11 Maths Chapter 1 Sets Miscellaneous Exercise PDF in Hindi and English Medium. Sets Class 11 Maths NCERT Solutions are extremely helpful while doing your homework. Sets Miscellaneous Exercise Class 11 Maths NCERT Solutions were prepared by Experienced LearnCBSE.in Teachers. Detailed answers of all the questions in Chapter 1 Class 11 Sets Miscellaneous Exercise provided in NCERT Textbook.
- Class 11 Sets Ex 1.1
- Class 11 Sets Ex 1.1 in Hindi Medium
- Class 11 Sets Ex 1.2
- Class 11 Sets Ex 1.2 Hindi Medium
- Class 11 Sets Ex 1.3
- Class 11 Sets Ex 1.3 Hindi Medium
- Class 11 Sets Ex 1.4
- Class 11 Sets Ex 1.4 Hindi Medium
- Class 11 Sets Ex 1.5
- Class 11 Sets Ex 1.5 Hindi Medium
- Class 11 Sets Ex 1.6
- Class 11 Sets Ex 1.6 Hindi Medium
- Class 11 Sets Miscellaneous Exercise
- Class 11 Sets Miscellaneous Exercise in Hindi Medium
- Sets Class 11 Notes Maths Chapter 1
- NCERT Exemplar Class 11 Maths Chapter 1 Sets
- RD Sharma Class 11 Solutions Chapter 1 Sets
- Chapter 1: Sets Class 11 NCERT Book
- अध्याय 1: समुच्चय Class 11 NCERT Book
Free download NCERT Solutions for Class 11 Maths Chapter 1 Sets Miscellaneous Exercise PDF in Hindi Medium as well as in English Medium for CBSE, Uttarakhand, Bihar, MP Board, Gujarat Board, BIE, Intermediate and UP Board students, who are using NCERT Books based on updated CBSE Syllabus for the session 2019-20.
Class 11 Maths NCERT Solutions Chapter 1 Sets Miscellaneous Exercise
Solution 1:
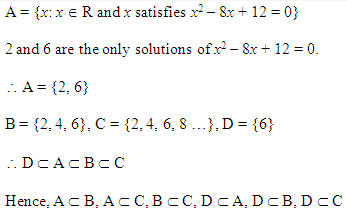
Solution 2:

Solution 3:
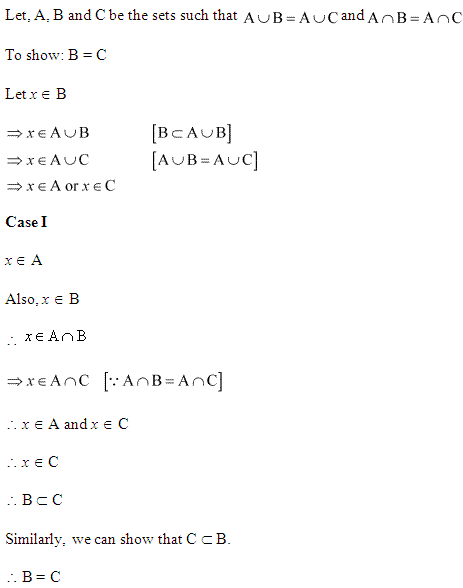
Solution 4:

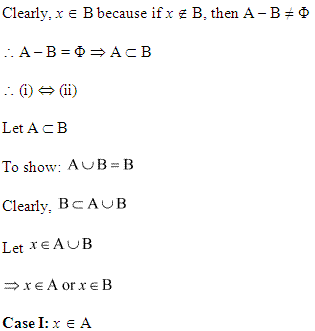

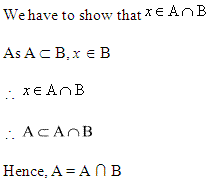
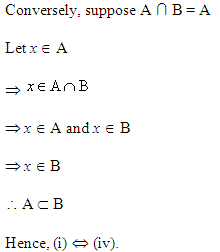
Solution 5:
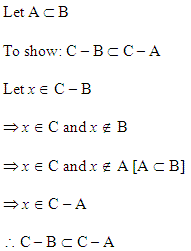
Solution 6:
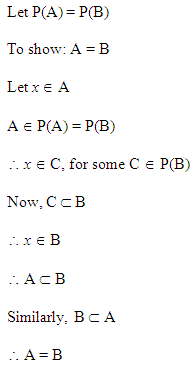
Solution 7:

Solution 8:
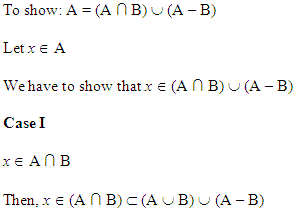
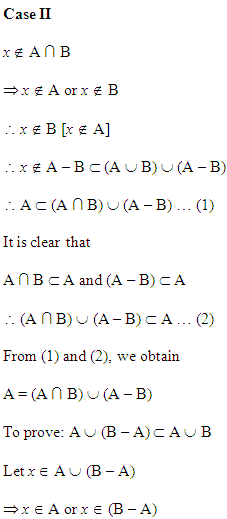
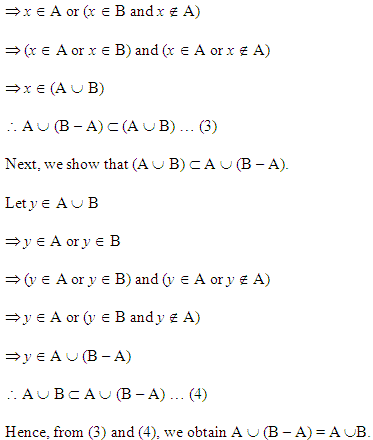
Solution 9:

Solution 10:
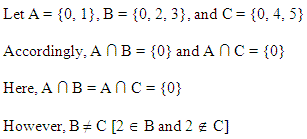
Solution 11:

Solution 12:
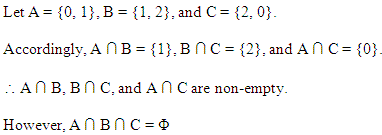
Solution 13:

Solution 14:

Solution 15:
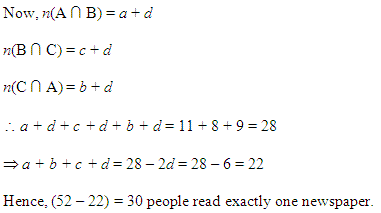
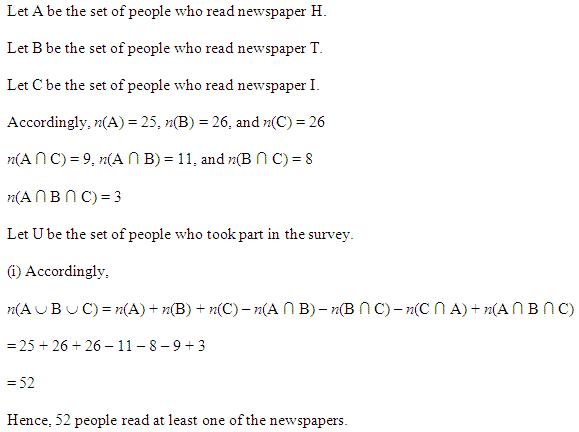
Solution 16:
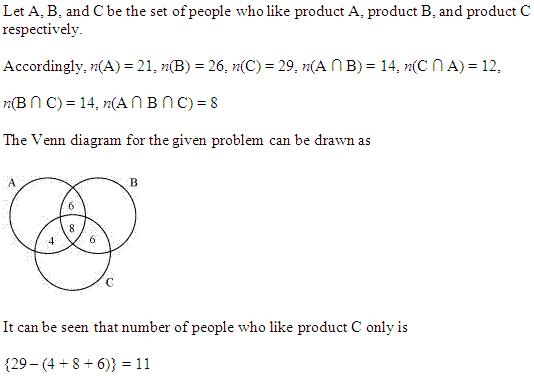
NCERT Solutions for Class 11 Maths Chapter 1 Sets Miscellaneous Exercise in Hindi


प्रश्न 3.
मान लीजिए A, B और Cऐसे समुच्चय हैं कि A ∪ B = A ∪ C तथा A ∩ B = A ∩ C, तो दर्शाइए कि B = C
हल:
दिया है:
A ∪ B = A ∪ C
(A ∪ B) ∩ C = (A ∪ C) ∩ C = C [(A ∪ C) ∩ C = C ]
(A ∩ C) ∩ (B ∩ C) = C
(A ∩ B) ∪ (B ∩ C) = C ….(i) [A ∩ C = A ∩ B = दिया है।]
A ∪ B = A ∪ C
(A ∪ B) ∩ B = (A ∪ C) ∩ B
B = (A ∪C) ∩ B = (A ∩ B) ∪ (C ∩ B)
या (A ∩ ) ∪ (B ∩ C) = B ……(ii)
(i) और (ii) से B = C प्राप्त होता है।
प्रश्न 4.
दिखाइए कि निम्नलिखित चार प्रतिबन्ध तुल्य हैं:
(i) A ⊂ B
(ii) A – B = Φ
(iii) A ∪ B = B
हल:
(i) A ⊂ B अर्थात् समुच्चय A के सभी अवयव B में हैं।
A – B = Φ अर्थात (i) ⇔ (ii)
(ii) A – B = Φ ⇔ समुच्चय A के सभी अवयव B में हैं।
A ∪ B = B
अर्थात (ii) ⇔ (iii)
(iii) A ∪ B = B ⇔ समुच्चय A के सभी अवयव B में है।
समुच्चय A और B मे समुच्चय A के अवयव उभयनिष्ठ है।
A ∩B = A
इससे स्पष्ट है सभी कथन समान हैं।
प्रश्न 5.
दिखाइए कि यदि A ⊂ B तो C – B ⊂ C – A.
हल:
मान लीजिए x ∈ C – B ⇒ x ∈ C पंरतु x ∈ B
दिया है: A ⊂ B ⇒ यदि x ∉ B ⇒ x ∉ A
अर्थात, x ∈ C और x ∉ A ⇒ x ∈ C – A
यहाँ हम पाते हैं कि
यदि x ∈ C – B तब x ∈ C – A
⇒ C – B ⊂ C – A.
प्रश्न 6.
मान लीजिए कि P(A) = P(B), सिद्ध कीजिए कि A = B.
हल:
मान लीजिए x, समुच्चय A का कोई अवयव है।
तब एक उपसमुच्चय X (मान लो) ऐसा होगा जिसमे x ∈ A जिसके अनुसार
X ⊂ A ⇒ X ∈ P(A)
X ∈ P(B) [P(A) = P(B)]
X ⊂ B या x ∈ B
अर्थात यदि
x ∈ A तब x ∈ B ⇒ A ∈ B …..(i)
y समुच्चय B का कोई अवयव हो, तब
समुच्चय B का कोई उपसमुच्चय Y (मान लो) होगा जिससे y ∈ Y
Y ⊂ B ⇒ Y ∈P(B)
Y ∈P(A) [P(A) = P(B)]
Y ⊂ A यदि y ∈ B तब y ∈ A
B ⊂ A ………(ii)
समीकरण (i) और (ii) से, हम पाते हैं।
A = B.
प्रश्न 7.
किन्हीं भी समुच्चयों A तक B के लिए क्या यह सत्य है कि P(A) ∪ P(B) = P(A ∪ B) ? अपने उत्तर का औचित्य बताइए।
हल:
मान लीजिए।
A = {a}, B = {b}, और A ∪ B = {a, b}
P(A) = {Φ, {a}}, P(B) = {Φ, {b}}
P(A) ∪ P(B) = {Φ, {4}, {5}} …(i)
अब A ∪ B = {a, b}
P(A ∪ B) = {Φ, {a}, {b}, {a, b}}
समी. (i) और (ii) से हम देखते हैं कि
अतः P(A) ∪ P(B) ≠ P(A ∪ B)
प्रश्न 8.
किन्हीं दो समुच्चयों A तथा B के लिए सिद्ध कीजिए कि
A = (A ∩ B) ∪ (A – B) और A ∪ (B – A) = A ∪ B.
हल:
(i) दायाँ पक्ष = (A ∩ B) ∪ (A – B)
= (A ∩ B) ∪ (A – B) [A – B = A ∩ B’]
= (A ∩ (B ∪ B’) (वितरण गुण से)
= A ∩ U (यहाँ U सार्वत्रिक समुच्चय)
= A
अतः (A ∩ B) ∪ (A – B) = A.
(ii) बायाँ पक्ष = A ∪ (B – A)
= A ∪ (B ∩ A’) [B – A = B ∩ A’]
= (A ∪ B) ∩ (A ∪ A’) (वितरण गुण से)
= (A ∪ B) ∩ U [यहाँ U सार्वत्रिक समुच्चय]
= A ∪ B
अतः : A ∪ (B – A) = A ∪ B
प्रश्न 9.
समुच्चयों के गुणधर्मों का प्रयोग करके सिद्ध कीजिए कि
(i) A ∪ (A ∩ B) = A
(ii) A ∩ (A ∪ B) = A.
हल:
(i) बायाँ पक्ष = A ∪ (A ∩ B)
= (A ∪ A) ∩ (A ∪ B) (वितरण गुण से)
= A ∩ (A ∪ B) (A ∪ A = A)
= A [A ⊂ A ∪ B]
A ∪ (A ∩ B) = A.
(ii) बायाँ पक्षु = A ∩ (A ∪ B)
= (A ∩ A) ∪ (A ∩ B) [वितरण गुण से]
= A ∪ (A ∩ B) [A ∩ A = A]
= A [A ∩ B ⊂ A]
अतः A ∩(A ∪ B) = A.
प्रश्न 10.
दिखलाइए कि A ∩ B = A ∩ C का तात्पर्य B = C आवश्यक रूप से नहीं होता।
हल:
मान लीजिए A = {1, 2}, B = {1, 7} तथा C = {1, 4} हो, तब
A ∩ B = {1, 2} ∩ {1, 7} = {1}
A ∩ C = {1, 2} ∩ {1, 4} = {1}
A ∩ B = A ∩ C
B ≠ C
यदि A ∩ B = A ∩ C तो आवश्यक नूह है कि B = C.
प्रश्न 11.
मान लीजिए कि A और B समुच्चय हैं। यदि किसी समुच्चय X के लिए A∪ X = B ∪ X = Φ तथा A ∪ X = B ∪ X तो सिद्ध कीजिए कि A = B.
हल:
दिया है A ∪ X = B ∪ X, जब कि X कोई समुच्चय है।
A ∩ (A ∪ X) = A ∩ (B ∪ X) [A ⊂ A ∪X, A ∩ (A ∪ X) = A]
A = A ∩ (B ∪ X)
= (A ∩ B) ∪ (A ∩ X) [वितरण गुण से]
= (A ∩ B) ∪ Φ (दिया है, A ∩ X = Φ
= A ∩ B
A ⊂ B ……(i)
A ∪ X = B ∪ X
B ∩(A ∪ X) = B ∩ (B ∪ X)
B ∩(A ∪ X) = B [B ⊂ B ∪ X]
(B ∩ A) ∪ (B ∩ X) = B [वितरण गुण से]
(B ∩ A) ∪ Φ = B [दिया है: B ∩ X = Φ]
(B ∩ A) = B
B ⊂ A …..(ii)
समी. (i) और (ii) से, हम पाते हैं कि A = B.
प्रश्न 12.
ऐसे समुच्चय A, B और C ज्ञात कीजिए ताकि A ∩ B, B ∩ C तथा A ∩ C आरिक्त समुच्चय हों और A ∩ B ∩ C = Φ.
हल:
मान लीजिए। A = {1, 2}, B = {2, 3}, C = {1, 3}
A ∩ B = {1, 2} ∩ {2, 3} = {2},
B ∩ C = {2, 3} ∩ {1, 3} = {3}
C ∩ A = {1, 3} ∩ {1, 2} = {1}
अतः A ∩ B, B ∩ C, C ∩ A रिक्त समुच्चय नहीं हैं।
A ∩ B ∩ C = (A ∩ B) ∩ C = {2} ∩ {1, 3} = Φ
इति सिद्धम्
प्रश्न 13.
किसी विद्यालय के 600 विद्यार्थियों के सर्वेक्षण से ज्ञात हुआ कि 150 विद्यार्थी चाय, 225 विद्यार्थी कॉफी तथा 100 विद्यार्थी चाय और कॉफी दोनों पीते हैं। ज्ञात कीजिए कि कितने विद्यार्थी न तो चाय पीते हैं और न कॉफी पीते हैं।
हल:
मान लीजिए 7 और C चाय तथा कॉफी पीने वाले विद्यार्थियों के समुच्चय हों, तब
n(T) = 150, n(C) = 225, n(T ∩ C) = 100
n(T ∪ C) = n(T) + n(C) – n(T ∩ C) = 150 + 225 – 100 = 275
= उन विद्यार्थियों की संख्या जो चाय या कॉफी पीते हैं या चाय और कॉफी दोनों पीते हैं।
विद्यार्थियों की कुल संख्या = 600
उन विद्यार्थियों की संख्या जो चाय या कॉफी कुछ भी नहीं पीते = 600 – 275 = 325.
प्रश्न 14.
विद्यार्थियों के समूह में, 100 विद्यार्थी हिन्दी, 50 विद्यार्थी अंग्रेजी तथा 25 विद्यार्थी दोनों भाषाओं को जानते हैं। विद्यार्थियों में से प्रत्येक या तो हिन्दी या अंग्रेजी जानता है। समूह में कुल कितने विद्यार्थी हैं?
हल:
पाना तथा क्रमशः हिन्दी और अंग्रेजी जानने वालों के समुच्चय हों, तब
n(H) = 100, n(E) = 50, n(H ∩ E) = 25
n(H ∪ E) = n(H) + n(E) – n(H ∩E) = 100 + 50 – 25 = 125
उन विद्यार्थियों की संख्या जो हिन्दी या अंग्रेजी जानते हैं = 125.
प्रश्न 15.
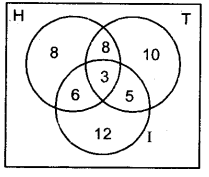
60 लोगों के सर्वेक्षण में पाया गया कि 25 लोग समाचार पत्र H, 26 लोग समाचार पत्र T, 26 लोग समाचार पत्र I, 9 लोग H तथा I दोनों, 11 लोग H तथा T दोनों, 8 लोग T तथा I दोनों और 3 लोग तीनों ही समाचार पत्र पढ़ते हैं, तो निम्नलिखित ज्ञात कीजिए:
(i) कम से कम एक समाचार पत्र पढ़ने वालों की संख्या।
(ii) ठीक ठीक केवल एक समाचार पत्र पढ़ने वालों की संख्या।
हल:
कुल लोगों की संख्या जिनका सर्वेक्षण किया गया = 60
H समाचार पत्र पढ़ने वालों की संख्या, n (H) = 25
T समाचार पत्र पढ़ने वालों की संख्या, n (T) = 26
I समाचार पत्र पढ़ने वालों की संख्या, n (I) = 26
H और I समाचार पत्र पढ़ने वालों की संख्या, n (H ∩ I) = 9
H और I समाचार पत्र पढ़ने वालों की संख्या, n (H ∩ T) = 11
T और I समाचार पत्र पढ़ने वालों की संख्या, n (T ∩ I) = 8
तीनों समाचार पत्र पढ़ने वालों की संख्या, n (H ∩ T ∩ I) = 3
H और I समाचार पत्र पढ़ने वाले तथा T समाचार पत्र न पढ़ने वालों की संख्या = 9 – 3 = 6
H और T समाचार पत्र पढ़ने वाले तथा I समाचार पत्र न पढ़ने वालों की संख्या = 11 – 3 = 8
T और I समाचार पत्र पढ़ने वाले तथा H समाचार पत्र न पढ़ने वालों की संख्या = 8 – 3 = 5
केवल H समाचार पत्र पढ़ने वालों की संख्या = 25 – 8 – 6 – 3 = 8
केवल T समाचार पत्र पढ़ने वालों की संख्या = 26 – 8 – 3 – 5 = 10
केवल I समाचार पत्रं पढ़ने वालों की संख्या = 26 – 6 – 3 – 5 = 12
कम से कम एकं समाचार पत्र पढ़ने वालों की संख्या = केवेल एक समाचार पत्र पढ़ने वालों की संख्या + केवल दो समाचार पत्र पढ़ने वालों की संख्या + तीनों समाचार पत्र पढ़ने वालों की संख्या = (8 + 10 + 12) + (8 + 6 + 5) + 3 = 30 + 19 + 3 = 52
वैकल्पिक विधि :
n(H ∪ T ∪ I) = n(H) + n(T) + n(I) – n(H ∩ T) – n(T ∩ I) – n(H∩I) + n(H ∩ T ∩ I)
= 25 + 26 + 26 – 11 – 8 – 9 + 3 = 77 – 28 + 3 = 80 – 28 = 52
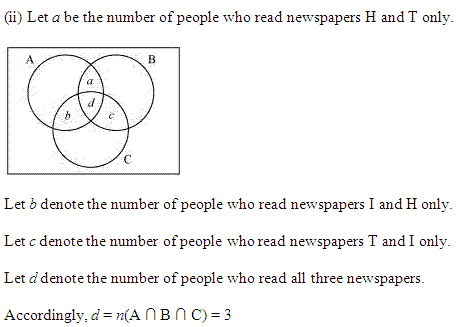
(ii) केवल H और T समाचार पत्र पढ़ने वालों की संख्या = 11 – 3 = 8
केवल T और 1 समाचार पत्र पढ़ने वालों की संख्या = 8 – 3 = 5
केवल 1 और H समाचार पत्र पढ़ने वालों की संख्या = 9 – 3 = 6
तीनों समाचार पत्र पढ़ने वालों की संख्या = 3
केवल एक समाचार पत्र पढ़ने वालों की संख्या = 52 – (8 + 5 + 6 + 3) = 52 – 22 = 30.
प्रश्न 16.
एक सर्वेक्षण में पाया गया कि 21 लोग उत्पाद A, 26 लोग उत्पाद B, 29 लोग उत्पाद C पसंद करते हैं। यदि 14 लोग उत्पाद A तथा B, 12 लोग उत्पाद C तथा A, 14 लोग उत्पाद B तथा C और 8 लोग तीनों ही उत्पादों को पसंद करते हैं। ज्ञात कीजिए कि कितने लोग केवल उत्पाद C को पसंद करते हैं?
हल:
दिया है:
n(A) = 21,
n(B) = 26,
n(C) = 29
n(A ∩ B) = 14,
n(A ∩ C) = 12
n(B ∩ C) = 14,
n(A ∩ B ∩ C) = 8
n(A ∩ C) = 12,
P(A ∩ B ∩ C) = 8
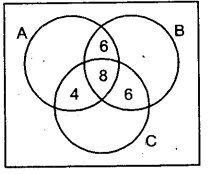
n(केवल A और C) = 12 – 8 = 4
n(केवल B और C) = 14 – 8 = 6
n(केवल C) = n(C) – n (केवल A और C) – n (केवल B और C) – n(A ∩ B ∩ C) = 29 – 4 – 6 – 8 = 29 – 18 = 11. .