NCERT Exemplar Class 8 Maths Chapter 11 Mensuration are part of NCERT Exemplar Class 8 Maths. Here we have given NCERT Exemplar Class 8 Maths Chapter 11 Mensuration.
NCERT Exemplar Class 8 Maths Chapter 11 Mensuration
Multiple Choice Questions
Question. 1 A cube of side 5 cm is painted on all its faces. If it is sliced into 1 cubic centimetre cubes, then how many 1 cubic centimetre cubes will have exactly one of their faces painted?
(a) 27 (b) 42 (c) 54 (d) 142
Solution.

Question. 2 A cube of side 4 cm is cut into 1 cm cubes. What is the ratio of the surface areas of the original cube and cut-out cubes?
(a) 1 : 2 (b) 1 : 3 (c) 1 : 4 (d) 1 : 6
Solution.

Question. 3 A circle of maximum possible size is cut from a square sheet of board. Subsequently, a square of maximum possible size is cut from the resultant circle. What will be the area of the final square?
(a) 3/4 of original square (b) 1/2 of original square
(c) 1/4 of original square (d) 2/3 of original square
Solution.
(b) Let a be the side of a square sheet.

Question.4 What is the area (in sq units) of the largest triangle, that can be fitted into a rectangle of length l units and width w units?
(a)lw/2 (b) lw/3 (c) lw/6 (d) lw/4
Solution.
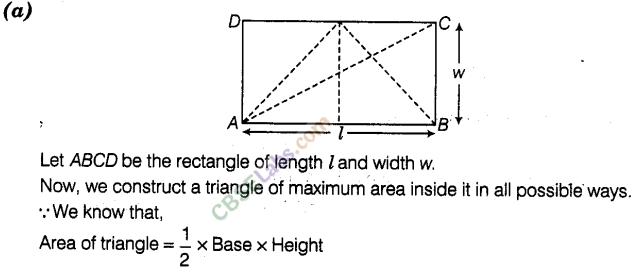
Question. 5 If the height of a cylinder becomes1/4 of the original height and the radius
is doubled, then which of the following will be true?
(a) Volume of the cylinder will be doubled
(b) Volume of the cylinder will remain unchanged
(c) Volume of the cylinder will be halved
(d) Volume of the cylinder will be 1/4 of the original volume
Solution.

Question. 6 If the height of a cylinder becomes 1/4 of the original height and the radius
is doubled, then which of the following will be true?
(a) Curved surface area of the cylinder will be doubled
(b) Curved surface area of the cylinder will remain unchanged
(c) Curved surface area of the cylinder will be halved
(d) Curved surface area will be 1/4 of the original curved surface
Solution.

Question. 7 If the height of a cylinder becomes 1/4 of the original height and the radius
is doubled, then which of the following will be true?
(a) Total surface area of the cylinder will be doubled
(b) Total surface area of the cylinder will remain unchanged
(c) Total surface area of the cylinder will be halved
(d) None of the above
Solution.

Question. 8 The surface area of the three coterminus faces of a cuboid are 6, 15 and 10 cm2, respectively. The volume of the cuboid is
(a) 30 Cm3 (b) 40 Cm3 (c) 20 Cm3 (d) 35 Cm3
Solution.

Question. 9 A regular hexagon is inscribed in a Circle of radius r. The perimeter of the regular hexagon is
(a) 3r (b) 6r (c)9r (d)12r
Solution.
(b) A regular hexagon comprises 6 equilateral triangles, each of them having one of their vertices at the centre of the hexagon.
The sides of the equilateral triangle are equal to the radius of the smallest circle inscribing the hexagon.
Hence, each side of the hexagon is equal to the radius of the hexagon and the perimeter of the hexagon is 6 r.
Question. 10 The dimensions of a godown are 40 m, 25 m and 10 m. If it is filled with . cuboidal boxes each of dimensions 2 m x 1.25 m x 1 m, then the number of boxes will be .
(a) 1800 (b) 2000 (c) 4000 (d) 8000
Solution.

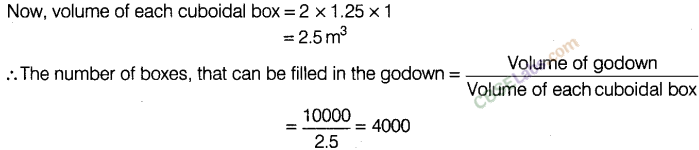
Question. 11 The volume of a cube is 64 cm3. Its surface area is
(a) 16 cm2 (b) 64 cm2
(c) 96 cm2 (d) 128 cm2
Solution.
(c) Let the side of the cube be a. Then,
Volume of cube = a3 = 64 [given]
⇒ a = 4
Now, surface area of the cube = a2 = 6 x 42 = 96 cm2
Question. 12 If the radius of a cylinder is tripled but its curved surface area is unchanged, then its height will be
(a) tripled , (b) constant
(c) one-sixth (d) one-third
Solution.

Question. 13 How many small cubes with edge of 20 cm each can be just accommodated in a cubical box of 2 m edge?
(a) 10 (b) 100 (c) 1000 (d) 10000
Solution.
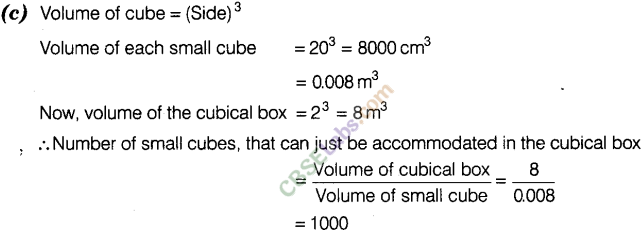
Question. 14 The volume of a cylinder whose radius r is equal to its height, is

Solution.
(c) Given, r = h
Then, volume of cylinder = πr2h = πr2r=πr3
Question. 15 The volume of a cube whose edge is 3x, is
(a) 27x3 (b) 9x3 (c)6x3 (d) 3x3
Solution.
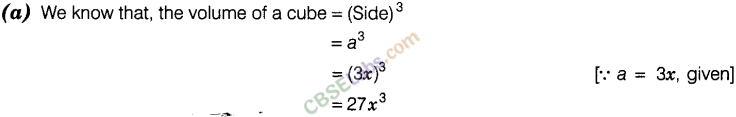
Question. 16 The figure ABCD is a quadrilateral, in which AB area is CD and BC = AD. Its area is
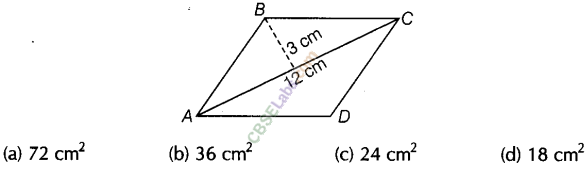
Solution.
Question. 17 What is the area of the rhombus ABCD below, if AC = 6 cm and BE = 4 cm?
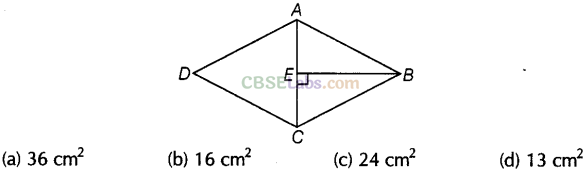
Solution.

Question. 18 The area of a parallelogram is 60 cm2 and one of its altitude is 5 cm. The length of its corresponding side is
(a) 12 cm (b)6 cm (c) 4 cm (d) 2 cm
Solution.

Question. 19 The perimeter of a trapezium is 52 cm and its each non-parallel side is equal to 10 cm with its height 8 cm. Its area is
(a) 124 cm2 (b) 118 cm2 (c) 128 cm2 (d) 112 cm2
Solution.
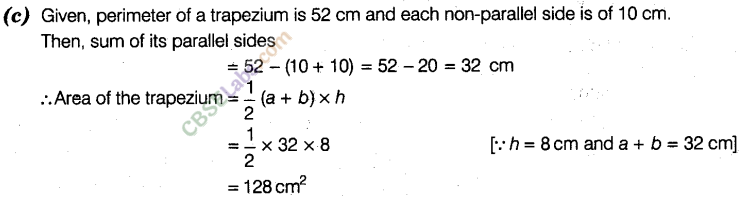
Question. 20 Area of a quadrilateral ABCD is 20 cm2 and perpendiculars on BD from opposite vertices are 1 cm and 1.5 cm. The length of BD is
(a) 4 cm (b) 15 cm (c) 16 cm (d) 18 cm
Solution.

Question. 21 A metal sheet 27 cm long, 8 cm broad and 1 cm thick is melted into a cube. The side of the cube is
(a) 6 cm (b) 8 cm (c) 12 cm (d) 24 cm
Solution.
(a) Given, a metal sheet 27 cm long, 8 cm broad and 1 cm thick.
Then, volume of the sheet (cubiodal) = l x b x h
=27 x 8 x 1 = 216 cm3
Now, since this sheet is melted to form a cube of edge length a (say).
Then, volume of the cube = Volume of the metal sheet
⇒ a3 =216 cm3
⇒ a = 6 cm
Hence, the side of the cube is 6 cm.
Question. 22 Three cubes of metal whose edges are 6 cm, 8 cm and 10 cm respectively, are melted to form a single cube. The edge of the new cube is
(a) 12 cm (b) 24 cm
(c) 18 cm (d) 20 cm
Solution.

Question. 23 A covered wooden box has the inner measures as 115 cm, 75 cm and 35 cm and thickness of wood as 2.5 cm. The volume of the wood is
(a) 85000 cm3 (b) 80000 cm3
(c) 82125 cm3 (d) 84000 cm3
Solution.

Question.24 The ratio of radii of two cylinders is 1: 2 and heights are in the ratio 2 : 3. The ratio of their volumes is
(a) 1 : 6 (b) 1 : 9 (c) 1 : 3 (d) 2 : 9
Solution.

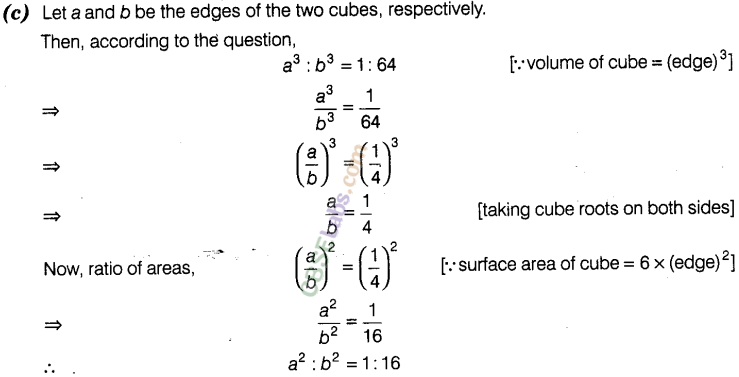
Question. 25 Two cubes have volumes in the ratio 1 : 64. The ratio of the areas of a face of first cube to that of the other is
(a) 1 : 4 (b) 1 : 8
(c) 1 : 16 (d) 1 : 32
Solution.
Question. 26 The surface areas of the six faces of a rectangular solid are 16, 16, 32, 32, 72 and 72 sq cm. The volume of the solid (in cu cm) is (a) 192 (b) 384 (c) 480 (d) 2592
Solution.

Question. 27 Ramesh has three containers.
(i) Cylindrical container A having radius r and height h.
(ii)Cylindrical container B having radius 2r and height 1/2 h.
(iii)Cuboidal container C having dimensions r x r x h.
The arrangement of the containers in the increasing order of their volumes is
(a)A,B,C (b) B, C, A
(c) C, A, B (d) Cannot be arranged
Solution.
(c) (i) The volume of the cylindrical container having radius r and height h
= πr2 h
(ii) The volume of the cylindrical container with radius 2 r and height 1/2
= π (2 r)2 x 1/2 h = π x 4 r2 x 1/2 h
‘ =2 πr2h
(iii) The volume of the cuboidal container having dimensions rxrxh
= r2 h
From parts (i), (ii) and (iii), we have the following order C, A, B.
Question. 28 If R is the radius of the base of the hat, then the total outer surface area of the hat is

Solution.

Fill in the Blanks
In questions 29 to 52, fill in the blanks to make the statements are true.
Question. 29 A cube of side 4 cm is painted on all its sides. If it is sliced in 1 cu cm cubes, then number of such cubes that will have exactly two of their faces painted, is_______.
Solution. 24
The volume of a cube of side 4 cm = 4 x 4 x 4 = 64cm3 When it is sliced into 1 cm3 cubes, we will get 64 small cubes.
In each side of the larger cube, the smaller cubes in the edges will have more than one face painted.
The cubes which are situated at the corners of the big cube, have three faces painted.
So, to each edge two small cubes are left which have two faces painted. As, the total number of edges in a cube are 12.
Hence, the number of small cubes with two faces painted = 12 x 2 = 24
Question. 30 A cube of side 5 cm is cut into 1 cm cubes. The percentage increase in volume after such cutting is_______.
Solution.

Question. 31 The surface area of a cuboid formed by joining two cubes of side a face-to-face, is_______.
Solution. 10a2
We have, two cubes of side a.
These two cubes are joined face-to-face, then the resultant solid figure is a cuboid which has same breadth and height as the joined cubes has length twice of the length of a cube, i.e. l = 2a,b= aandh = a
Thus, the total surface area of the cuboid = 2 (lb + bh + hi)
= 2 (2a x a + a x a + a x 2a)
= 2 (2 a2 + a2 + 2 a2)=2 x 5 a2 = 10a2
Question. 32 If the diagonals of a rhombus get doubled, then the area of the rhombus becomes_______its original area.
Solution.

Question. 33 If a cube fits exactly in a cylinder with height h, then the volume of the cube is_______and_______surface area of the cube is .
Solution. h3 ,6h2
Since, the cube fits exactly in the cylinder with height h, therefore each side of the cube = h
Now, volume of the cube = (Side)3 = h3
and surface area of the cube = 6 x (Side)2
=6 x h2
Question. 34 The volume of a cylinder becomes_______the original volume, if its
radius becomes half of the original radius.
Solution.

Question. 35 The curved surface area of a cylinder is reduced by_______per cent, if
the height is half of the original height.
Solution.

Question. 36 The volume of a cylinder which exactly fits in a cube of side a, is _______.
Solution.
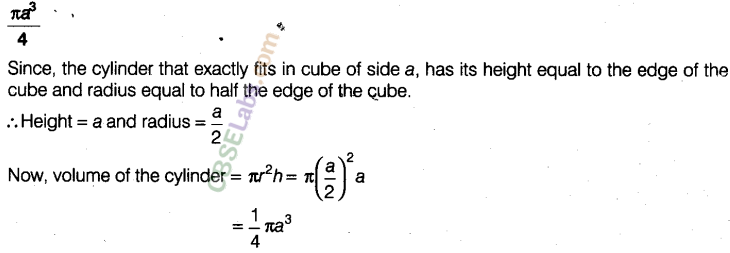
Question. 37 The curved surface area of a cylinder which exactly fits in a cube of side b, is _______.
Solution.
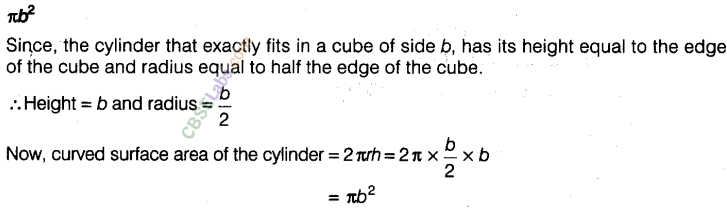
Question. 38 If the diagonal d of a quadrilateral is doubled and the heights h1 and h2
falling on d are halved, then the area of quadrilateral is _______.
Solution.

Question. 39 The perimeter of-a-rectangle becomes_______times its original
perimeter, if its length and breadth are doubled.
Solution. 2 times
Perimeter of a rectangle with length l and breadth b = 2(l + b)
If the length and the breadth are doubled, then the new perimeter
= 2(2l + 2b)
= 2[2(l + b)]
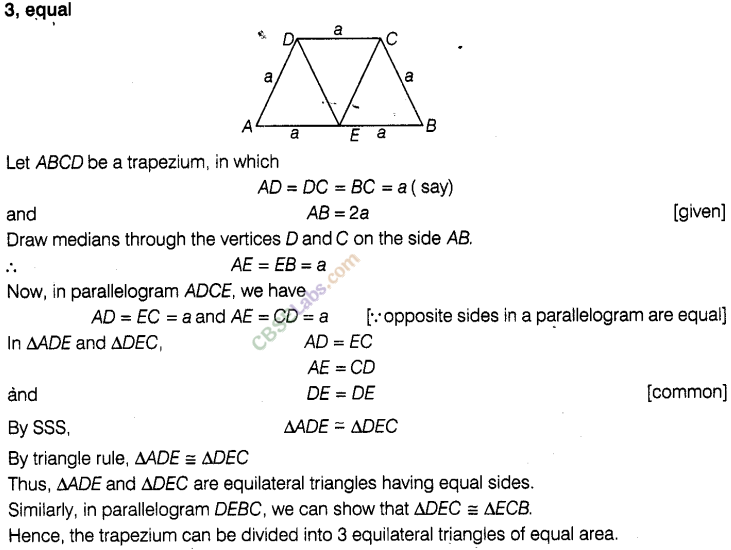
Question. 40 A trapezium with 3 equal sides and one side double the equal side, can be divided into_______ equilateral triangles of_______area.
Solution.
Question. 41 All six faces of a cuboid are_______in shape and of_______area.
Solution. rectangular, different
We know that, a cuboid is made of 6 rectangular plane regions, i.e. 6 rectangular faces, which have different lengths and breadths Therefore the area of the rectangular faces are different. .
Question.42 Opposite faces of a cuboid are_______in area.
Solution. equal
We know that, a cuboid has 6 rectangular races, of which opposite faces have the same length and breadth. Therefore, area of the opposite faces are equal.
Question.43 Curved surface area of a cylinder of radius h and height r is_______.
Solution. 2πhr (or) 2πrh
We know that, the curved surface area of a cylinder of radius h and height r
= 2π x Radius x Height .
= 2π x h x r=2πhr
= 2πrh
Question.44 Total surface area of a cylinder of radius h and height r is_______ .
Solution. 2πh(r+ h)
Given, radius of cylinder = h and height of cylinder = r
...Total surface area of a cylinder = Curved surface area + Area of top surface + Area of base
= 2 x π x Radius x Height + π (Radius)2+ π (Radius)2
= 2πhr+ πh2 + πh2
= 2πrh + 2πh2
= 2πh(r + h)
Question.45 Volume of a cylinder with radiusT? and height r is_______.
Solution. πh2r
Given, radius of cylinder = h and height of cylinder = r.
Now, volume of a cylinder
= π x (Radius)2 x Height =π x h2 x r = πh2r
Question.46 Area of a rhombus = 1/2 product of_______.
Solution. diagonals
We know that, the area of a rhombus = Half of the product of its diagonals
=1/2 [Product of diagonals]
Question. 47 Two cylinders A and B are formed by folding a rectangular sheet of dimensions 20 cm x 10 cm along its length and also along its breadth, respectively. Then, volume of A is_______of volume of B.
Solution.

Question. 48 In the above question, curved surface area of A is_______surface area of B.
Solution.

Question. 49_______of a solid is the measurement of the space occupied by it.
Solution. Volume
We know that, a solid always occupies some space and magnitude of this space region is known as the volume of the solid.
Question. 50_______surface area of room = Area of 4 walls.
Solution. Lateral
We know that, a room is in the shape of a cuboid. Its 4 walls are treated as lateral faces of the cuboid.
... Lateral surface area of room = Area of 4 walls
Question. 51 Two cylinders of equal volume have heights in the ratio 1: 9. The ratio of their radii is_______.
Solution.

Question. 52 Two cylinders of same volume have their radii in the ratio 1 : 6. Then, ratio of their heights is_______.
Solution.

True/False
In questions 53 to 61, state whether the statements are True or False.
Question. 53 The areas of any two faces of a cube are equal.
Solution. True
Since, all the faces of a cube are squares of same side length, therefore the areas of any two faces of a cube are equal.
Question. 54 The areas of any two faces of a cuboid are equefl.
Solution. False
A cuboid has rectangular faces with different lengths and breadths. Only opposite faces of cuboid have the same length and breadth.
Therefore, areas of only opposite faces of a cuboid are equal.
Question. 55 The surface area of a cuboid formed by joining face-to-face 3 cubes of side x is 3 times the surface area of a cube of side x.
Solution. False
Three cubes having side x are joined face-to-face, then the cuboid so formed has the same height and breadth as the cubes but its length will be thrice that of the cubes.
Hence, the length, breadth and height of the cuboid so formed are 3x, x and x, respectively. Then, its surface area = 2 (lb + bh + hl)
= 2(3x x x + x x x + x x 3 x )=2(3x2 + x2 + 3x2)
= 2 x 7x2 = 14x2
Now, the surface area of the cube of side x = 6 (Side)2 = 6x2 Hence, the statement is false.
Question. 56 Two cuboids with equal volume will always have equal surface area.
Solution.

Question. 57 The area of a trapezium becomes 4 times, if its height gets doubled.
Solution. False
We know that,
Area of a trapezium = 1/2 (a + b) x h
where, a and b are the lengths of parallel sides and h is the altitude (height).
Now, if the height gets doubled, then
Area of trapezium = 1/2(a + b) x 2h = 2(1/2(a + b) x h)
Hence, the area is doubled.
So, the statement is false.
Question. 58 A cube of side 3 cm painted on all its faces, when sliced into 1 cu cm cubes, will have exactly 1 cube with none of its faces painted.
Solution. True
Given, a cube of side 3 cm is painted on all its faces. Now, it is sliced into 1 cu cm cubes. Then, there will be 8 corner cubes that have 3 sides painted, 6 centre cubes with only one side painted and only 1 cube in the middle that has no side painted.
Question. 59 Two cylinders with equal volume will always have equal surface area.
Solution. False

Question. 60 The surface area of a cube formed by cutting a cuboid of dimensions 2 x 1 x 1 in 2 equal parts, is 2 sq units.
Solution. False
The dimensions of the given cuboid are 2 x 1 x 1. It is sliced into two equal parts, which are cubes.
Then, the dimensions of the cube, so formed are 1 x 1 x 1.
...The surface area of the cube so formed = 6 (Side)2 = 6 x (1)2 = 6sq units
Hence, the surface area of the sliced cube is 6 sq units.
Question.61 Ratio of area of a circle to the area of a square whose side equals radius of circle, is 1 : TC.
Solution. False
Given, side of a square equals radius of a circle.
Then, area of the square = r2
and area of the circle =πr2
where r is a radius of the circle.
Now, the ratio of area of the circle to area of the square = πr2: r2 = π : 1.
Question. 62 The area of a rectangular field is 48 m2 and one of its sides is 6m. How long will a lady take to cross the field diagonally at the rate of 20 m/min?
Solution.

Question. 63 The circumference of the front wheel of a cart is 3 m long and that of the back wheel is 4 m long. What is the distance travelled by the cart, when the front wheel makes five more revolutions than the rear wheel?
Solution.
Given, circumference of front wheel = 3 m
Now, distance covered by front wheel of the cart in 1 revolution
= Circumference of front wheel .
... Distance covered by front wheel in 5 revolutions = 3 x 5 = 15 m
Hence, the distance covered by the cart is 15 m.
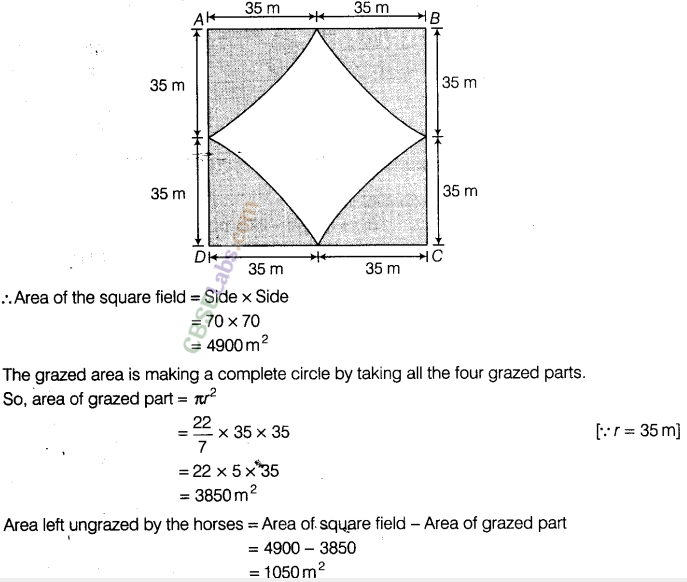
Question. 64 Four horses are tethered with equal ropes at 4 corners of a square field of side 70 m, so that they just can reach one-another. Find the area left ungrazed by the horses.
solution.
Given, side of a square = 70 m
Also, four horses are tethered with equal ropes at 4 corners of the square field. Hence, each horse can graze upto 35 m of distance along the side.
Question. 65 The walls and ceiling of a room are to be plastered. The length, breadth and height of the room are 4.5 m, 3m and 350 cm, respectively. Find the cost of plastering at the rate of ? 8 per m2.
solution.

Question. 66 Most of the sailboats have two sails, the jib and the mainsail. Assume that the sails are triangles. Find the total area of each sail of the sailboats to the nearest tenth.
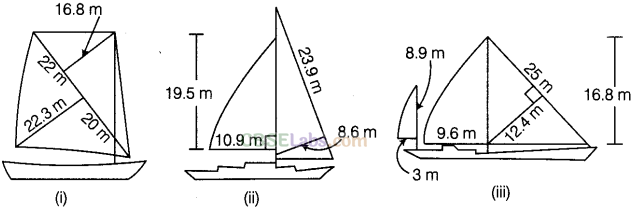
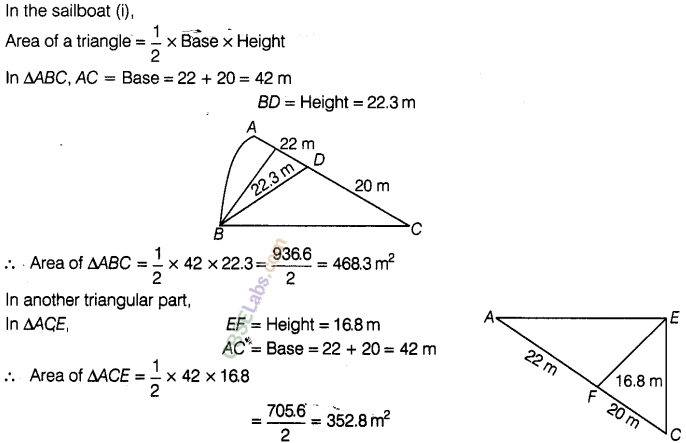
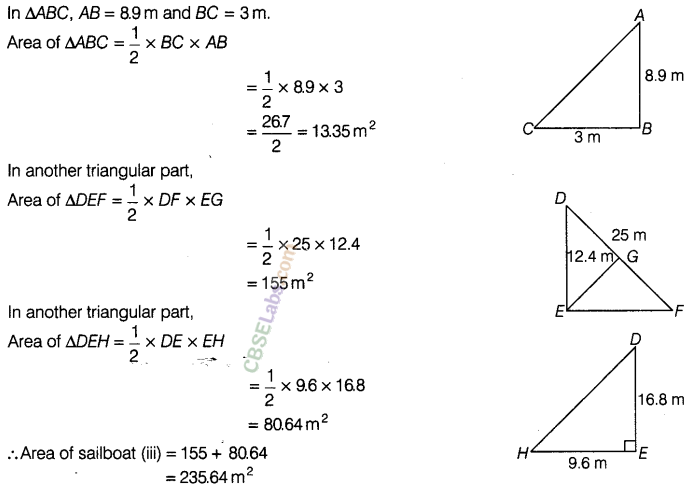
solution.

Question. 67 The area of a trapezium with equal non-parallel sides is 168 m2. If the lengths of the parallel sides are 36 m and 20 m, then find the length of the non-parallel sides.
solution.
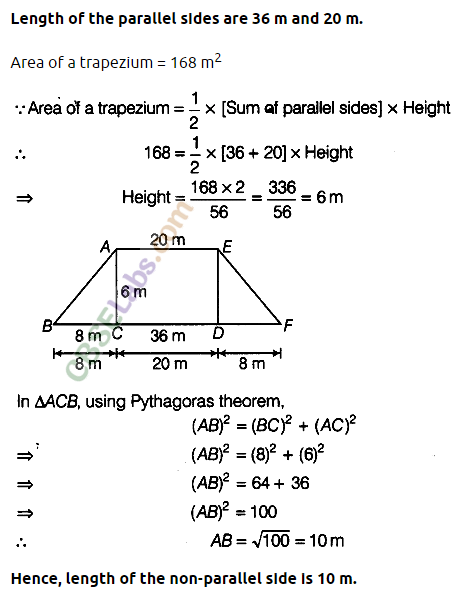
Question. 68 Mukesh walks around a circular track of radius 14 m with a speed of 4 km/h. If he takes 20 rounds of the track, for how lontj does he walk?
solution.

Question. 69 The areas of two circles are in the ratio 49 : 64. Find the ratio of their circumferences.
solution.

Question. 70 There is a circular pond and a footpath runs along its boundary. A person walks around it, exactly once keeping close to the edge. If his step is 66 cm long and he takes exactly 400 steps to go around the pond, then find the diameter of the pond.
solution.


Question. 71 A running track has 2 semi-circular ends of radius 63 m and two straight lengths. The perimeter of the track is 1000 m. Find each straight length.
solution.

Question. 72 Find the perimeter of the given figure.
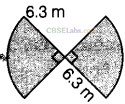
solution.

Question. 73 A bicycle wheel makes 500 revolutions in moving 1 km. Find the diameter of the wheel.
solution.

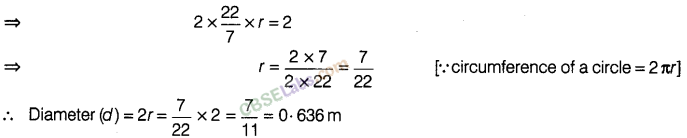
Question. 74 A boy is cycling such that the wheels of the cycle are making 140 revolutions per hour. If the diameter of the wheel is 60 cm, then calculate the speed (in km/h) with which the boy is cycling.
solution.

Question. 75 Find the length of the largest pole, that can be placed in a room of dimensions 12 mx 4 m x 43 m.
solution.
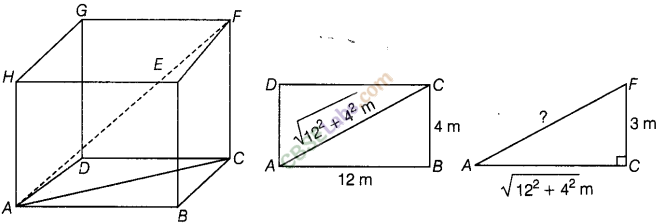
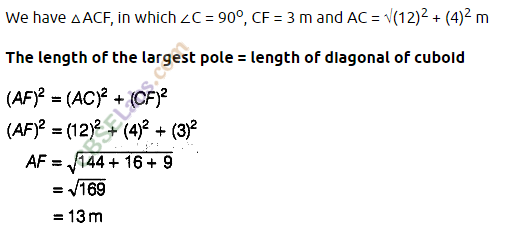
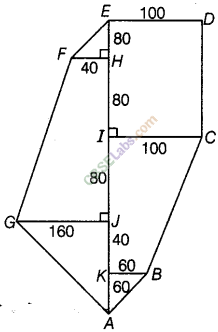
Question. 76 Find the area of the following fields. All dimensions are in metres.
solution.


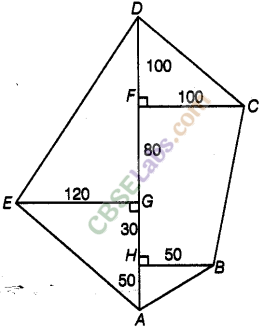
Question. 77 Find the area of the following fields. All dimensions are in metres.
solution.


In questions from 78 to 85, find the area of the shaded portion in the following figures.
Question. 78
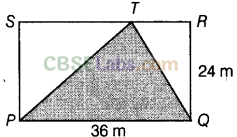
solution.

Question. 79
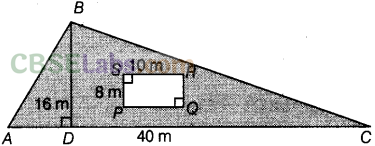
solution.

Question.80
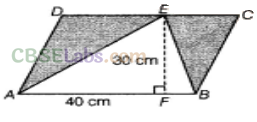
solution.

Question.81
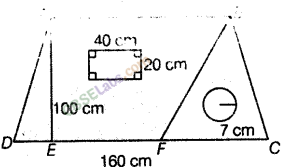
solution.

Question.82
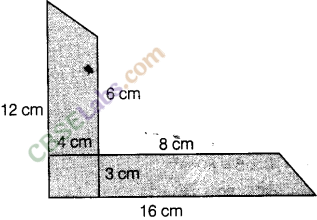
solution.
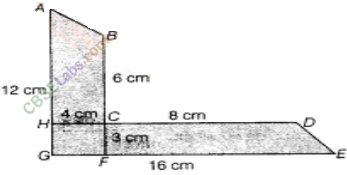

Question.83
solution.

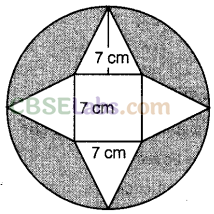
Question.84
solution.

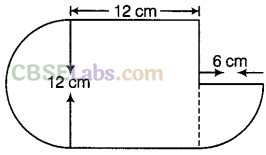
Question.85
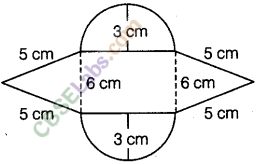
solution.

Question.86 Find the volume of each of the given figure, if Volume = Base area x Height
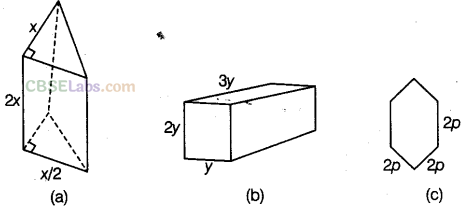
solution.

Question.87 A cube of side 5 cm is cut into as many 1 cm cubes as possible. What is the ratio of the surface areas of the original cube to that of the sum of the surface areas of the smaller cubes?
solution.
Surface area of a cube = 6 a2, where a is side of a cube.
... Side of cube = 5cm
... Surface area of the cube = 6 x (5)2 = 6 x 25
= 150cm2
Now, surface area of the cube with side 1 cm = 6 x (1)2= 6 cm2
... Surface area of 5 cubes with side 1 cm = 5 x 6 = 30 cm2
Ratio of the surface area of the original cube to that of the sum of the surface area of the smaller cubes
=30/150=3/15=1:5
Question. 88 A square sheet of paper is converted into a cylinder by rolling it along its side. What is the ratio of the base radius to the side of the square?
solution.
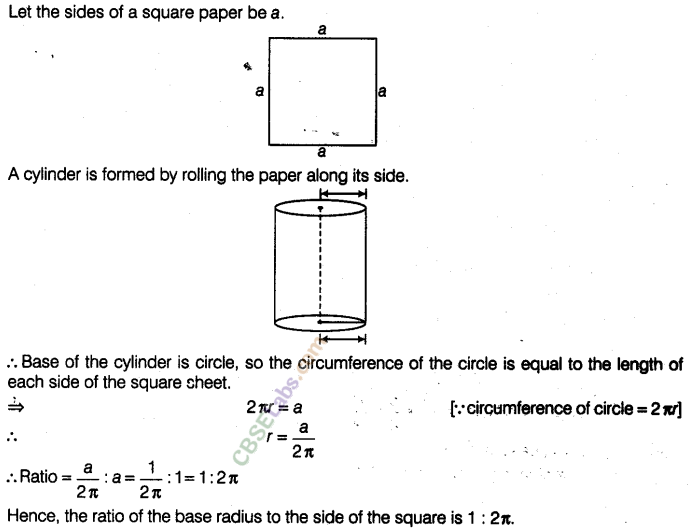
Question. 89 How many cubic metres of Earth must be dug to construct a well 7 m deep and of diameter 2.8 m?
solution.

Question. 90 The radius and height of a cylinder are in the ratio 3 : 2 and its volume is 19404 cm3. Find its radius and height.
solution.

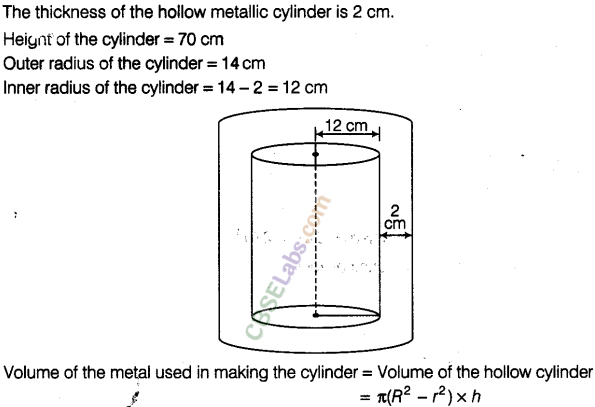
Question. 91 The thickness of a hollow metallic cylinder is 2 cm. It is 70 cm long with outer radius of 14 cm. Find the volume of the metal used in making the cylinder, assuming that it is open at both the ends. Also, find its weight if the metal weighs 8 g per cm3.
solution.
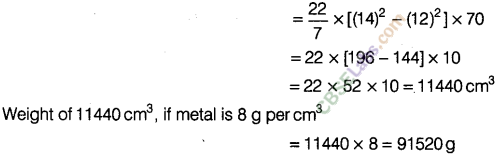
Question. 92 Radius of a cylinder is r and the height is h. Find the change in the volume if the
(i) height is doubled.
(ii)height is doubled and the radius is halved.
(iii)height remains
solution.

Question. 93 If the length of each edge of a cube is tripled, what will be the change in its volume?
solution.
Let the edge of a cube be a.
If edge of the cube became tripled i.e. a = 3 x a = 3a
... Volume of the cube = a3
... Volume of the cube with edge tripled = (3a)3 = 27 a3
Hence, volume is 27 times of the original volume.
Question. 94 A carpenter makes a box which has a volume of 13400 cm3 . The base has an area of 670 cm2 . What is the height of the box?
solution.

Question. 95 A cuboidal tin’ box opened at the top has dimensions 20 cm x 16 cm x 14 cm. What is the total area of metal sheet required to make 10 such boxes?
solution.
Dimensions of cuboidal tin box are20 cm x 16cm x 14 cm,
...Area of metal sheet for 1 box = Surface area of cuboid
= 2(lb + bh+hl)
= 2(20 x 16+16 x 14+ 14 x 20)
= 2(320 + 224 + 280)
= 2(824)
= 1648 c m2
... Area of metal sheet required to make 10 such boxes = 10 x 1648= 16460c m2
Question. 96 Find the capacity of water tank, in litres, whose dimensions are 4.2 m, 3 m and 1.8 m?
solution.

Question. 97 How many cubes each of side 0.5 cm are required to build a cube of volume 8 cm3?
solution.

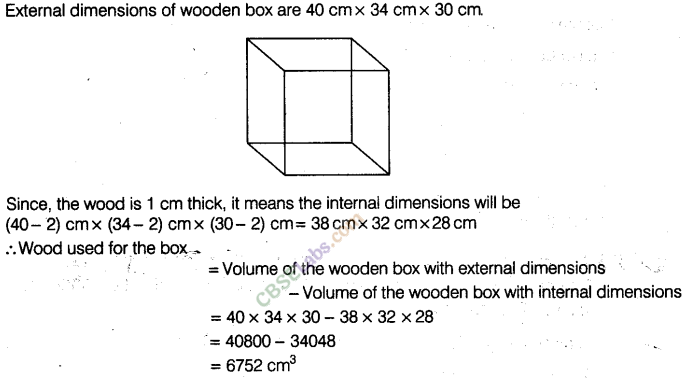
Question. 98 A wooden box (including the lid) has external dimensions
40 cm x 34 cm x 30 cm. If the wood is 1 cm thick, how many cm3 of wood is used in it?
solution.
Question.99 A river 2 m deep and 45 m wide is flowing at the rate of 3 km per hour. Find the amount of water in cubic metres that runs into the sea per minute.
solution.

Question.100 Find the area to be painted in the following block with cylindrical hole. Given that, length is 15cm, width 12cm, height 20cfn and radius of the hole 2.8 Cm.
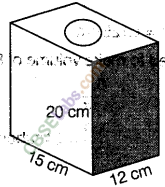
solution.

Question. 101 A truck carrying 7.8 m3 concrete arrives at a job site. A platform of width 5 m and height 2 m is being constructed at the site. Find the length of the platform, constructed from the amount of concrete on the truck?
solution.

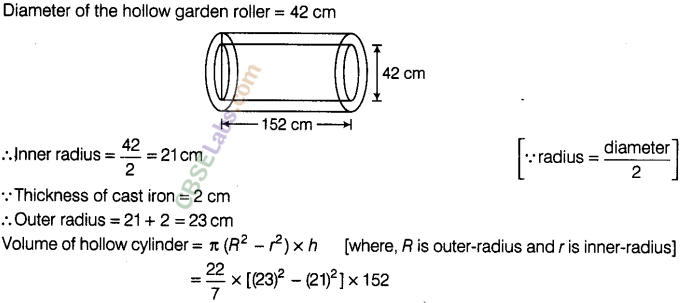
Question. 102 A hollow garden roller of 42 cm diameter and length 152 cm is made of cast iron 2 cm thick. Find the volume of iron used in the roller.
solution.
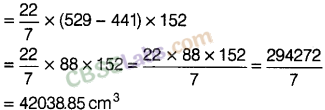
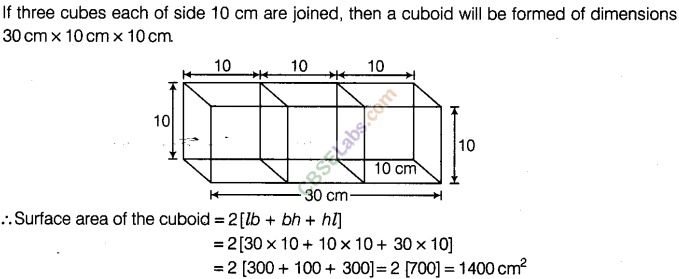
Question. 103 Three cubes each of side 10 cm are joined end to end. Find the surface area of the resultant figure.
solution.
Question. 104 Below are the drawings of cross sections of two different pipes used to fill swimming pools. Figure A is a combination of 2 pipes each having a radius of 8 cm. Figure B is a pipe having a radius of 15 cm. If the force of the flow of water coming out of the pipes is the same in both the cases, which will fill the swimming pool faster?
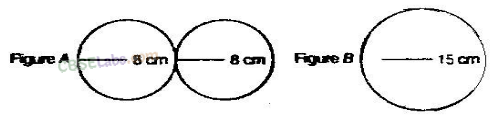
solution.

Question. 105 A swimming pool is 200 m x 50 m and has an average depth of 2 m. By the end of a summer day, the water level drops by 2 cm. How many cubic metres of water is lost on the day?
solution.

Question. 106 A housing society consisting of 5500 peoples needs 100 L of water per person per day. The cylindrical supply tank is 7 m high and has a diameter 10 m. For how many days will the water in the tank last for
the society?
solution.

Question. 107 Metallic discs of radius 0.75 cm and thickness 0.2 cm are melted to
obtain 508.68 cm3 of metal. Find the number of disc melted (Use π = 3.14)
Solution.


Question. 108 The ratio of the radius and height of a cylinder is 2:3. If its volume is 12936 cm3 find the the total surface area of the cylinder.
solution.

Question. 109 External dimensions of a closed wooden box are in the ratio 5:4:3. If the cost of painting its outer surface at the rate of Rs 5 per dm2is Rs 11750, find the dimensions of the box.
solution.

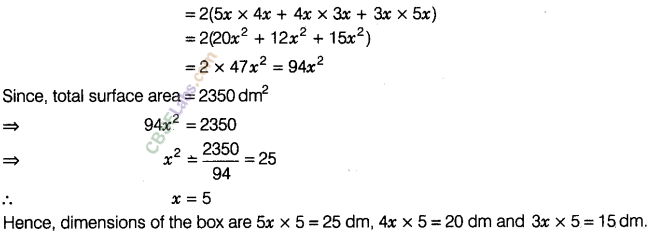
Question. 110 The capacity of a closed cylindrical vessel of height 1 m is 15.4 L. How many square metres of metal sheet would be needed to make it?
solution.

Question. 111. What will happen to the volume of the cube, if its edge
(a) tripled (b) reduced to one-fourth?
solution.
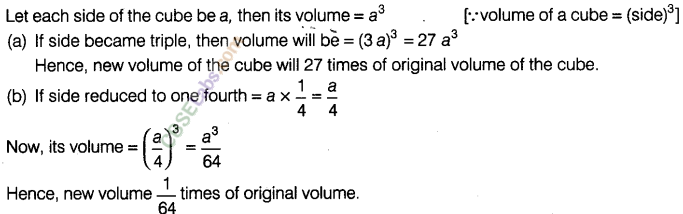
Question. 112 A rectangular sheet of dimensions 25 cm x 7 cm is rotated about its . longer side. Find the volume and the whole surface area of the solid thus generated.
solution.

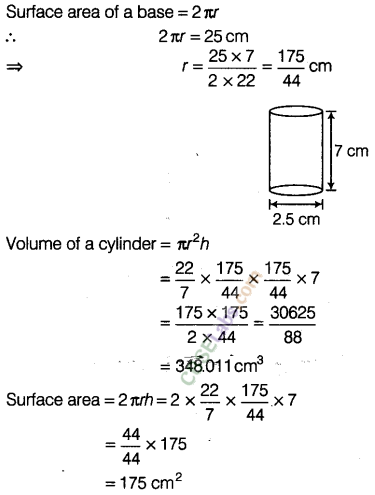
Question. 113 From a pipe of inner radius 0.75 cm, water flows at the rate of 7 m per second. Find the volume in litres of water delivered by the pipe in 1 h.
solution.

Question. 114 Four times the area of the curved surface of a cylinder is equal to 6 times the sum of the areas of its bases. If its height is 12 cm, find its curved surface area.
solution.
Let the radius and height of the cylinder be r and h, respectively.
Curved surface area of cylinder = 2 πrh
Area of base = πr2
Sum of areas of bases = 2 πr2

Question. 115 A cylindrical tank lias a radius of 154 cm. It is filled with water to a height of 3 m. If water to a height of 4.5 m is poured into it, what will be the increase in the volume of water in kL?
solution.

Question. 116 The length, breadth and height of a cuboidal reservoir is 7 m, 6 m and 15 m respectively. 8400 L of water is pumped out from the reservoir. Find the fall in the water level in the reservoir.
solution.

Question. 117 How many bricks of size 22 cm x 10 cm x 7 cm are required to
construct a wall 11 m long, 3.5 m high and 40 cm thick, if the cement and sand used in the construction occupy (1/10)th part of
the wall?
solution.

Question. 118 A rectangular examination hall having seats for 500 candidates has to be built so, as to allow 4 cubic metres of air and 0.5 square metres of floor area per candidate. If the length of hall be 25 m, find the height and breadth of the hall.
solution.

Question. 119 The ratio between the curved surface area and the total surface area of ‘ a right circular cylinder is 1: 2. Find the ratio between the height and
radius of the cylinder.
solution.

Question. 120 A birthday cake has two tiers as shown in the figure below. Find the volume of the cake.
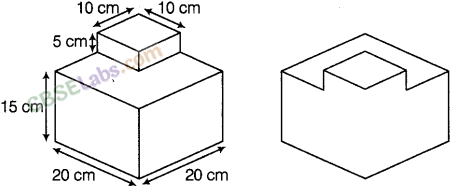
solution.
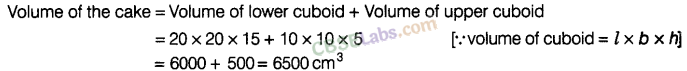
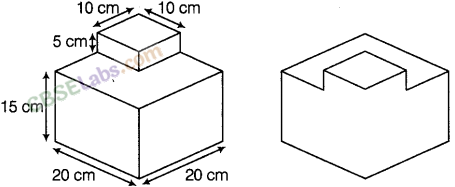
Question. 121
Solution.
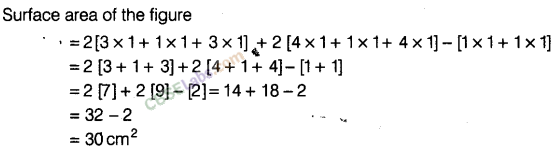
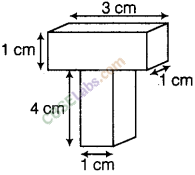
Question. 122
Solution.

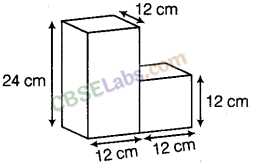
Question. 123
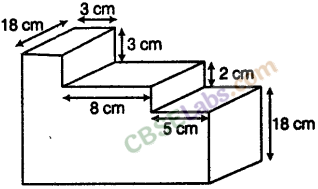
Solution.
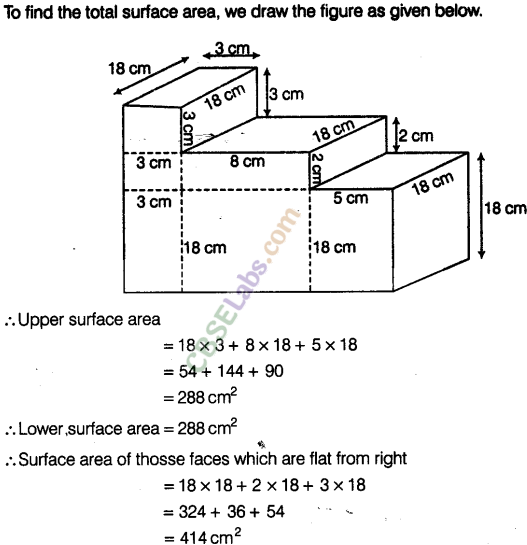
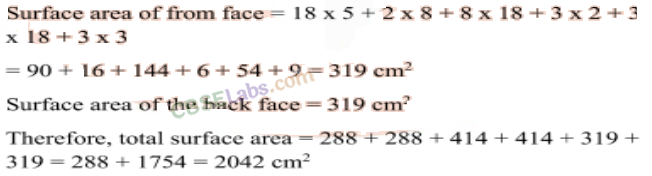
Question. 124
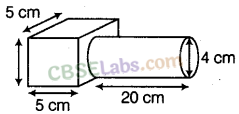
Solution.

Question. 125 Water flows from a tank with a rectangular base measuring 80 cm x 70 cm into another tank with a square base of side 60 cm. If the water in the first tank is 45 cm deep, how deep will it be in the second tank?
solution.

Question. 126 A rectangular sheet of paper is rolled in two different ways to form two different cylinders. Find the volume of cylinders in each case if the sheet measures 44 cm x 33 cm.
solution.
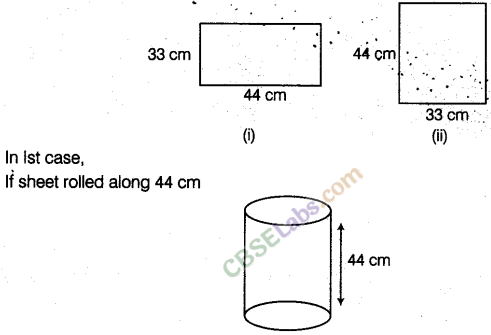
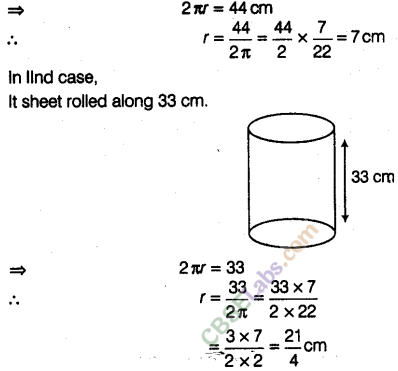
NCERT Exemplar Class 8 Maths Solutions
- Chapter 1 Rational Numbers
- Chapter 2 Data Handling
- Chapter 3 Square-Square Root and Cube-Cube Root
- Chapter 4 Linear Equations in One Variable
- Chapter 5 Understanding Quadrilaterals and Practical Geometry
- Chapter 6 Visualising Solid Shapes
- Chapter 7 Algebraic Expressions, Identities and Factorisation
- Chapter 8 Exponents and Powers
- Chapter 9 Comparing Quantities
- Chapter 10 Direct and Inverse Proportion
- Chapter 11 Mensuration
- Chapter 12 Introduction to Graphs
- Chapter 13 Playing with Numbers
We hope the NCERT Exemplar Class 8 Maths Chapter 11 Mensuration help you. If you have any query regarding NCERT Exemplar Class 8 Maths Chapter 11 Mensuration, drop a comment below and we will get back to you at the earliest.