NCERT Exemplar Problems Class 12 Mathematics Chapter 3 Matrices
Short Answer Type Questions
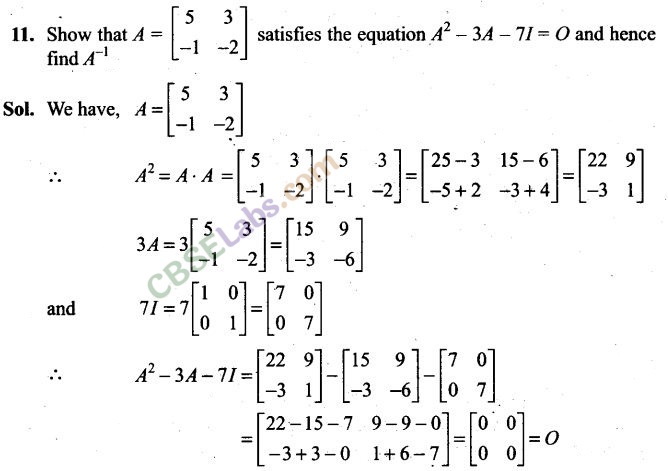
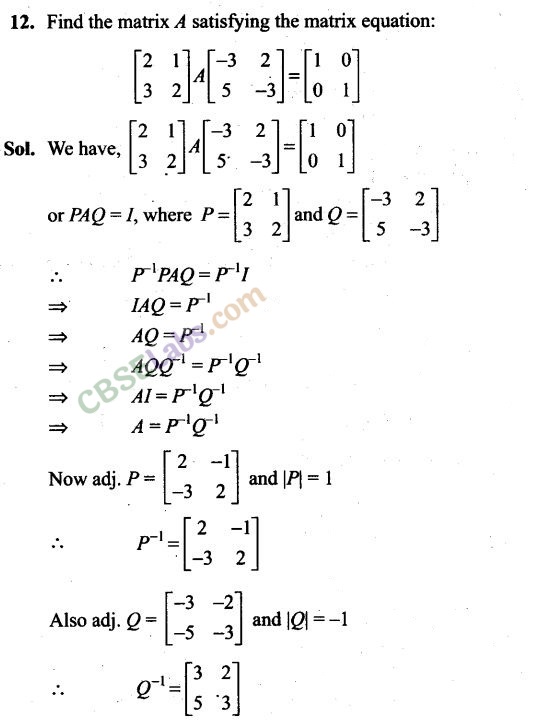
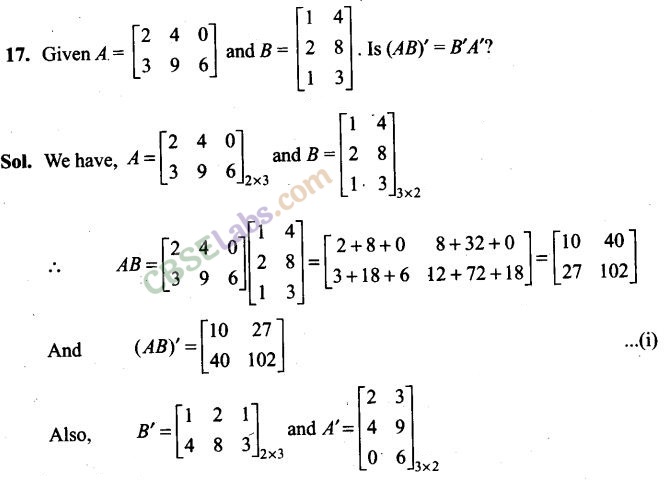
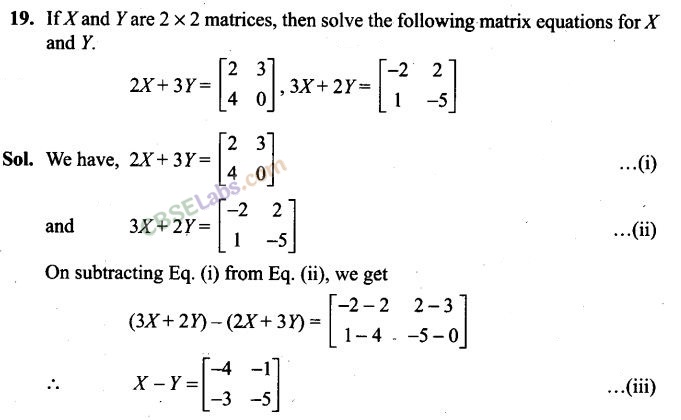
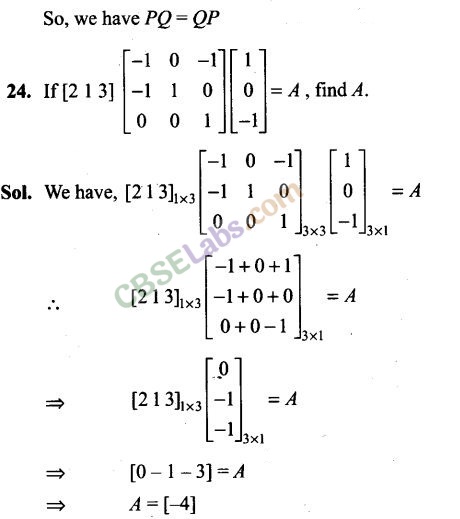
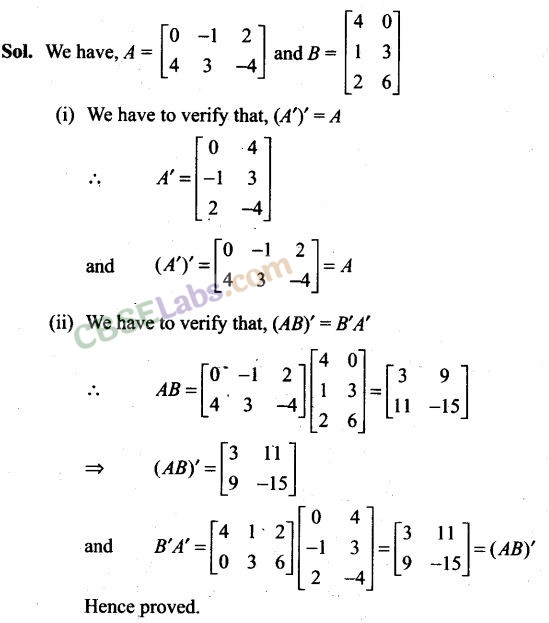
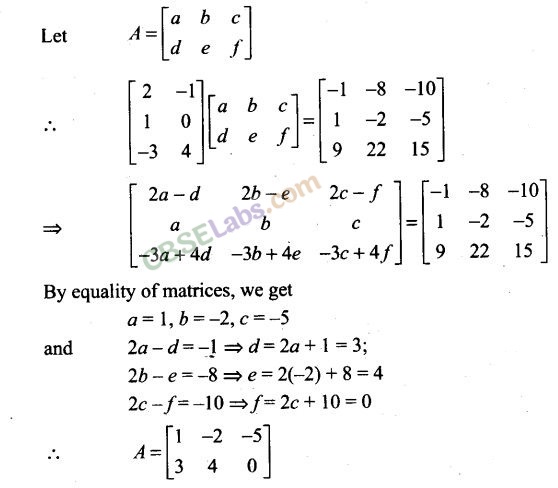
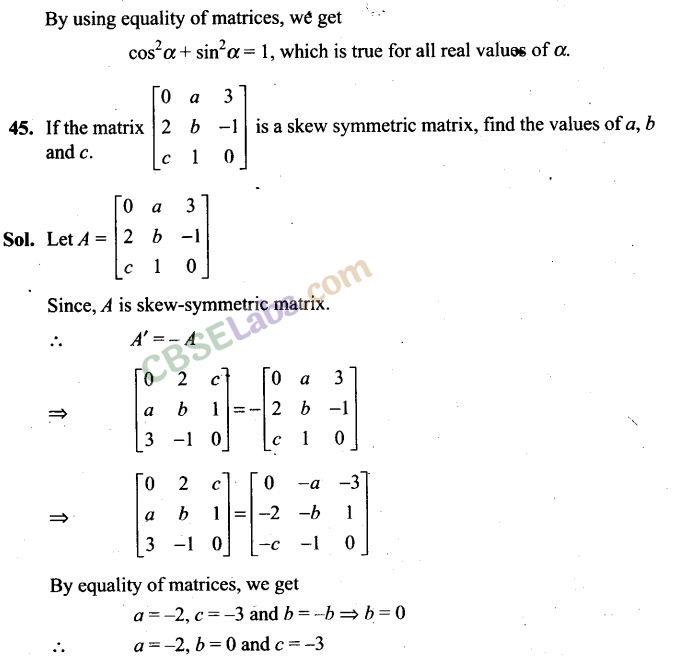
Long Answer Type Questions
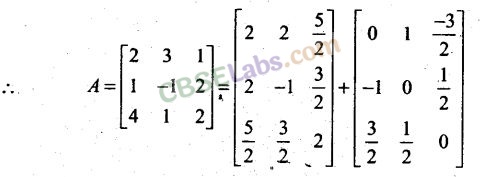
Objective Type Questions
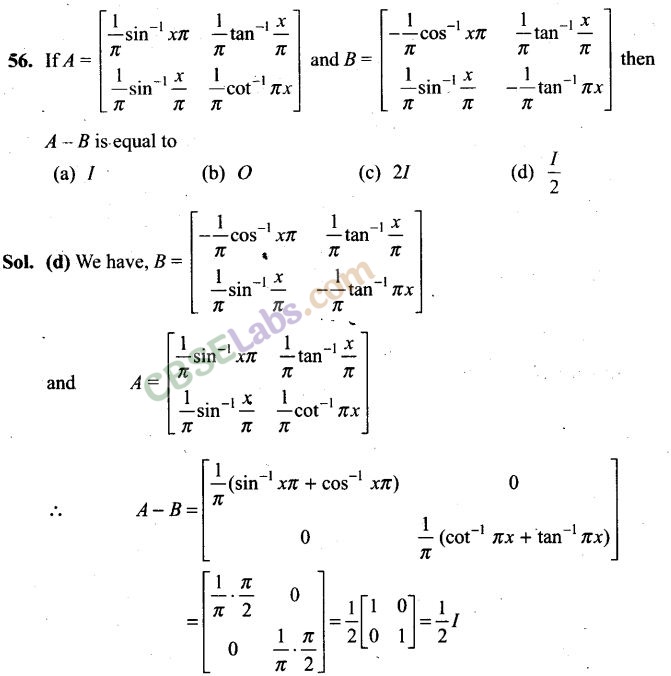
Fill In the Blanks Type Questions
True/False Type Questions
82. A matrix denotes a number.
Sol. False
A matrix is an ordered rectangular array of numbers of functions.
83. Matrices of any order can be added.
Sol. False
Two matrices are added, if they are of the same order.
84. Two matrices are equal if they have same number of rows and same number of columns.
Sol. False
If two matrices have same number of rows and same number of columns, we cannot say two matrices are equal as their corresponding elements may be different.
85. Matrices of different order cannot be subtracted.
Sol. True
Two matrices of same order can be subtracted
86. Matrix addition is associative as well as commutative.
Sol. True
Matrix addition is associative as well as commutative i.e.,
(A + B) + C = A + (B + C) and A + B = B + A, where A, B and C are matrices of same order.
87. Matrix multiplication is commutative.
Sol. False
If AB is defined, it is not necessary that BA is defined.
Also if AB and BA are defined, it not”necessary that they have same order. Further if AB and BA are defined and have same order, it is not necessary their corresponding elements are equal.
So, in general AB^BA
88. A square matrix where every element is unity is called an identity matrix.
Sol. False
Since, in an identity matrix, the diagonal elements are one and rest are all zero.
89. If A and B are two square matrices of the same order, then A + B = B + A.
Sol. True
Since, matrix addition is commutative i.e., A + B = B +A, where A and B are two square matrices.
90. If A and B are two matrices of the same order, then A-B = B-A.
Sol. False
A-B = -(B-A)
Thus A-B≠B-A
However when A – B = B – A
A-B = 0 or A =B
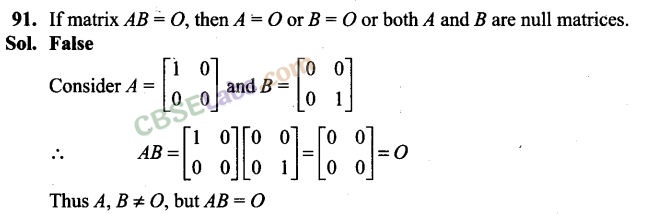
92. Transpose of a column matrix is a column matrix. False
Sol.Transpose of a column matrix is a row matrix.
93. If A and B are two square matrices of the same order, then AB = BA. False
Sol.For two square matrices of same order it is not always true that AB = BA.
NCERT Exemplar ProblemsMathsPhysicsChemistryBiology