NCERT Exemplar Class 12 Maths Chapter 12 Linear Programming are part of NCERT Exemplar Class 12 Maths. Here we have given Exemplar Problems for Class 12 Maths Chapter 12 Linear Programming PDF.
NCERT Exemplar Class 12 Maths Chapter 12 Linear Programming
NCERT Exemplar Class 12 Maths Chapter 12 Linear Programming Solutions is given below.
Short Answer Type Questions
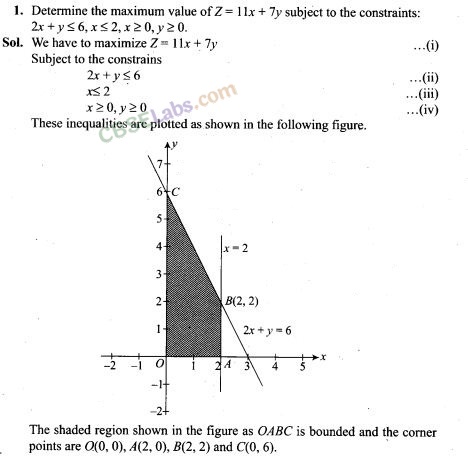
4. Minimize Z = 13x- 15y subject to the constraints: x+y≤ 7,2x-3y + 6 ≥ 0, x ≥ 0, y ≥ 0.
Sol. We have to Minimize Z = 13x – 15y subject to the constraints x + y ≤7, 2x – 3y + 6 ≥ 0, x ≥ 0, y ≥ 0. These inequalities are plotted as shown in the following figure.
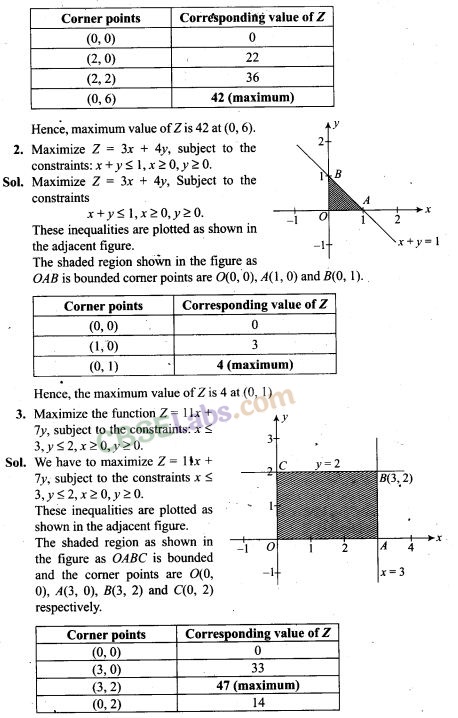
8. Refer to Exercise 7 above. Find the maximum value of Z.
Sol. Z is maximum at (3,2) and its maximum value is 47.
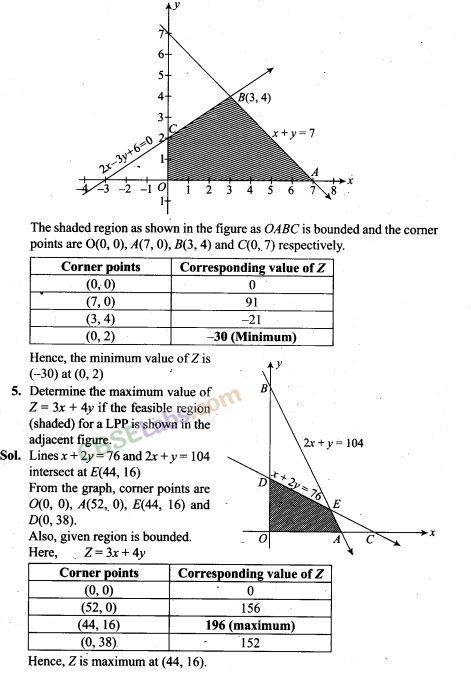
9. The feasible region for a LPP is shown in the following figure. Evaluate Z = 4x+y at each of the comer points of this region. Find the minimum value of Z, if it exists.
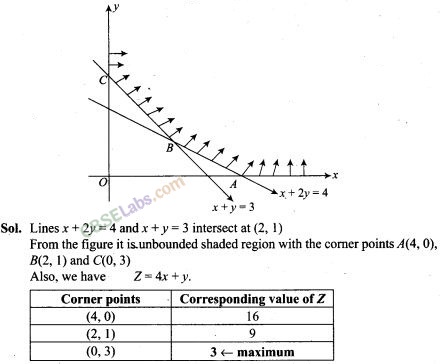
Now, we see that 3 is the smallest value of Z the comer point (0, 3). Note that here we see that, the region is unbounded, therefore 3 may not be the minimum value of Z. To decide this issue, we graph the inequality 4x + y < 3 and check whether the resulting open half plane has no point in common with feasible region otherwise, Z has no minimum value.
From the shown graph above, it is clear that there is no point in common with feasible region and hence Z has minimum value 3 at (0, 3).
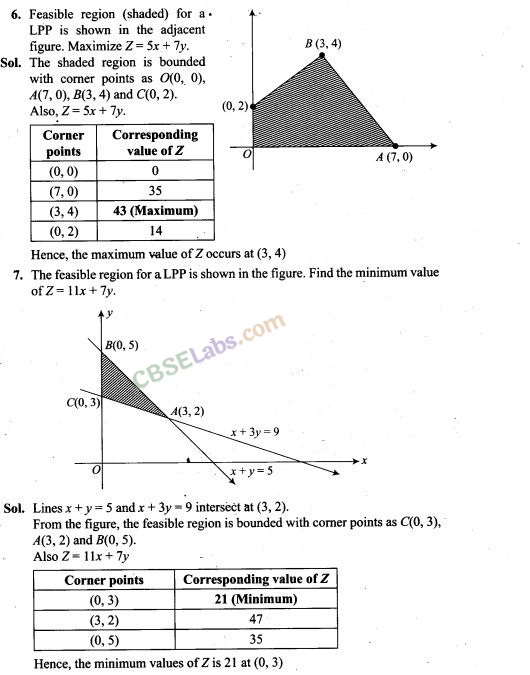
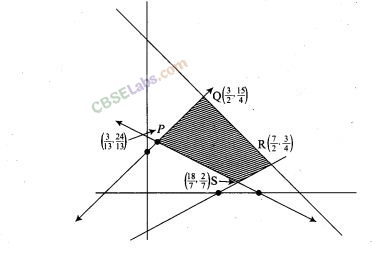
10. In the following figure, the feasible region (shaded) for a LPP is shown. Determine the maximum and minimum value of Z = x + 2y

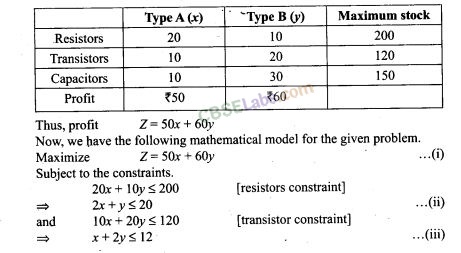
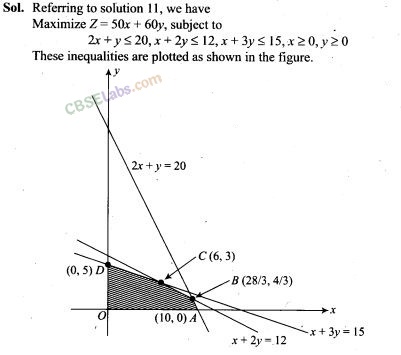
11. A manufacturer of electronic circuits has a stock of 200 resistors, 120 transistors and 150 capacitors and is required to produce two types of circuits A and B. Type A requires 20 resistors, 10 transistors and 10 capacitors. Type B requires 10 resistors, 20 transistors and 30 capacitors. If the profit on type A circuit is Rs 50 and that on type B circuit is Rs 60, formulate this problem as a LPP so that the manufacturer can maximise his profit.
Sol. Let the manufacture produces x units of type A circuits and y units of type B circuits. Form the given information, we have following corresponding constraint table.

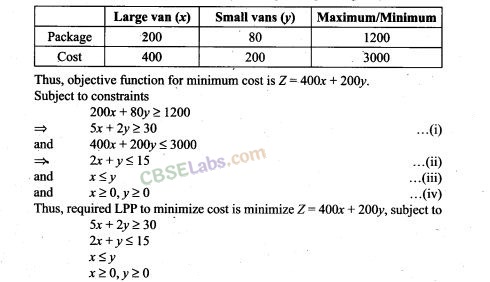
12. A firm has to transport 1200 packages using large vans which can carry 200 packages each and small vans which can take 80 packages each. The cost for engaging each large van is Rs 400 and each small van is Rs 200. Not more than Rs 3000 is to be spent on the job and the number of large vans can not exceed the number of small vans. Formulate this problem as a LPP given that the objective is to minimise cost.
Sol. Let the firm has x number of large vans and y number of small vans.
From the given information, we have following corresponding constraint table.
13. A company manufactures two types of screws A and B. All the screws have to pass through a threading machine and a slotting machine. A box of Type A screws requires 2 minutes on the threading machine and 3 minutes on the slotting machine. A box of type B screws requires 8 minutes of threading on the threading machine and 2 minutes on the slotting machine. In a week, each machine is available for 60 hours. On selling these screws, the company gets a profit of Rs 100 per box on type A screws and Rs 170 per box on type B screws. Formulate this problem as a LPP given that the objective is to maximise profit.
Sol. Let the company manufactures x boxes of type A screws and y boxes of type B screws.
From the given information, we have following corresponding constraint table.
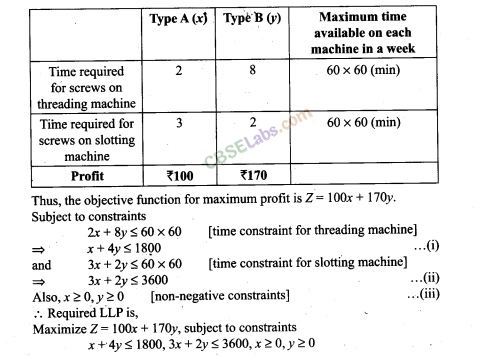
14. A company manufactures two types of sweaters: type A and type B. It costs Rs 360 to make a type A sweater and Rs 120 to make a type B sweater. The company can make at most 300 sweaters and spend at most Rs 72000 a day. The number of sweaters of type B cannot exceed the number of sweaters of type A by more than 100. The company makes a profit of Rs 200 for each sweater of type A and ?120 for every sweater of type B. Formulate this problem as a LPP to maximise the profit to the company.
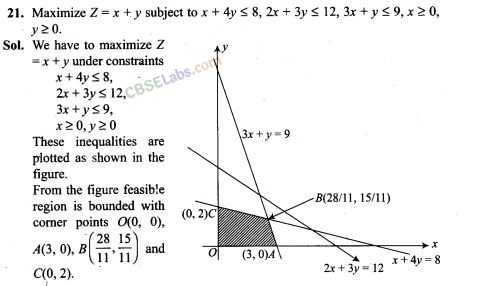
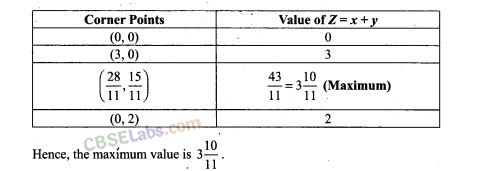
Sol. Let the company manufactures x number of type A sweaters and y number of type B.
The company spend at most Rs 72000 a day.
∴ 360x + 120y ≤ 72000
=> 3x+y≤ 600 …(i)
Also, company can make at most 300 sweaters.
∴ x+y≤ 300 …(ii)
Also, the number of sweaters of type B cannot exceed the number of sweaters of type A by more than 100 i.e., y-x≤ 100
The company makes a profit of Rs 200 for each sweater of type A and Rs 120 for every sweater of type B
So, the objective function for maximum profit is Z = 200x + 120y subject to constraints.
3x+y≤ 600
x+y ≤ 300
x-y ≥ -100
x ≥ 0, y ≥ 0
15. A,man rides his motorcycle at the speed of 50 km/hour. He has to spend Rs 2 per km on petrol. If he rides it at a faster speed of 80 km/hour, the petrol cost increases to Rs 3 per km. He has atmost Rs120 to spend on petrol and one hour’s time. He wishes to find the maximum distance that he can travel. Express this problem as a linear programming problem.
Sol. Let the man rides to his motorcycle to a distance x km at the speed of 50 km/h and to a distance y km at the speed of 80 km/h.
Therefore, cost on petrol is 2x + 3y.
Since, he has to spend Rs120 atmost on petrol.
∴ 2x + 3y ≤ 120 …(i)
Also, he has at most one hour’s time.
![]()
![]()
Long Answer Type Questions
16. Refer to Exercise 11. How many of circuits of Type A and of Type B, should be produced by the manufacturer so as to maximize his profit? Determine the maximum profit.




22. A manufacturer produces two Models of bikes’-Model X and Model Y. Model X takes a 6 man-hours to make per unit, while Model Y takes 10 man-hours per unit. There is a total of 450 man-hour available per week. Handling and Marketing costs are Rs 2000 and Rs 1000 per unit for Models X and Y respectively. The total funds available for these purposes are Rs 80,000 per week. Profits per unit for Models X and Y are Rs 1000 and Rs 500, respectively. How many bikes of each model should the manufacturer produce so as to yield a maximum profit? Find the maximum profit.

So, for maximum profit manufacture must produces 25 number of models X and 30 number of model Y bikes.
23. In order to supplement daily diet, a person wishes to take some X and some Y tablets. The contents of iron, calcium and vitamins in X and Y (in milligrams per tablet) are given as below:
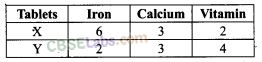
The person needs at least 18 milligrams of iron, 21 milligrams of calcium and 16 milligram of vitamins. The price of each tablet of X and Y is Rs 2 and Rs 1 respectively. How many tablets of each should the person take in order to satisfy the above requirement at the minimum cost?
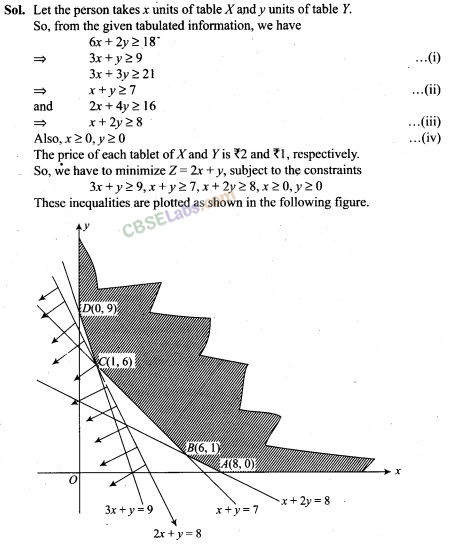
From the figure, we can see the feasible region is unbounded region, with comer points as A(%, 0), B(6,1), C(I, 6), and D(0, 9)

Thus, the minimum value of Z is ‘8’ occurring at B( 1, 6). Since the feasible region is unbounded, ‘8’ may not be the minimum value of Z. To decide this, we plot the inequality 2x+y < 8 and check whether the resulting open half has points common with feasible region or not If it has common point, then 8 will not be the minimum value of Z, otherwise 8 will be the minimum value of Z. Thus, from the graph it is clear that, it has no common point.
Therefore, Z= 2x+y-has 8 as minimum value subject to the given constrains. Hence, the person should take 1 unit of X tablet and 6 units of Y tablets to satisfy the given requirements and at the minimum cost of Rs 8.
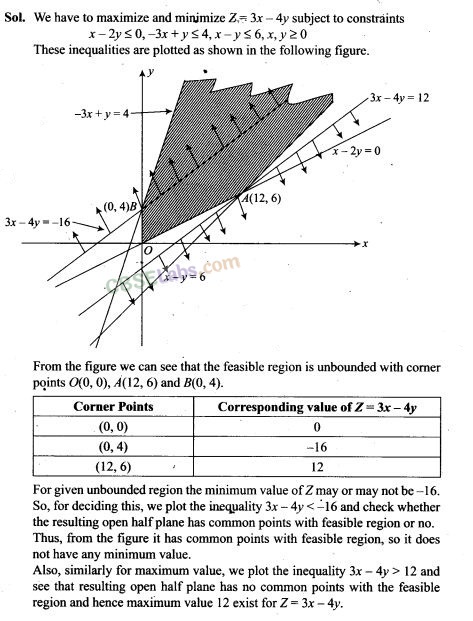
24. A company makes 3 models of calculators: A, B and C at factory I and factory II. The company has orders for at least 6400 calculators of model A, 4000 calculator of model B and 4800 calculator of model C. At factory I, 50 calculators of model A, 50 of model B and 30 of model C are made every day; at factory II, 40 calculators of model A, 20 of model B and 40 of model C are made everyday. It costs Rs 12000 and Rs 15000 each day to operate factory I and II, respectively. Find the number of days each factory should operate to minimize the operating costs and still meet the demand.


Objective Type Questions
26. The comer points of the feasible region determined by the system of linear constraints are (0,0), (0,40), (20,40), (60,20), (60,0). The objective function is Z=4x + 3y.
Compare the quantity in Column A and Column B
Column A Column B
Maximum of Z 325
(a) The quantity in column A is greater
(b) The quantity in column B is greater
(c) The two quantities are equal
(d) The relationship can not be determined on the basis of the information supplied .
Sol. (b)

28. Refer to Exercise 27. Maximum of Z occurs at
(a) (5,0) (b) (6,5) (c) (6, 8) (d) (4, 10)
Sol. (a) Refer to solution 27, maximum of Z occurs at (5, 0)
29. Refer to Exercise 27. (Maximum value of Z + Minimum value of Z) is equal to
(a) 13 (b) 1 (c) -13
Sol. (d) Refer to solution 27,
maximum value of Z + minimum value of Z = 15-32 = -17

31. Refer to Exercise 30. Minimum value of F is
(a) 0 (b) -16 . (c) 12 (d) does not exist
Sol. (b) Referring to solution 30, minimum value of F is -16 at (0,4).
32. Comer points of the feasible region for an LPP are (0, 2), (3, 0), (6,0), (6, 8) and (0,5).
Let F = 4x + 6y be the objective function.
The Minimum value of F occurs at
(a) (0,2) only
(b) (3,0) only
(c) the mid point of the line segment joining the points (0,2) and (3,0) only
(d) any point on the line segment joining the points (0,2) and (3, 0).
Sol. (d)
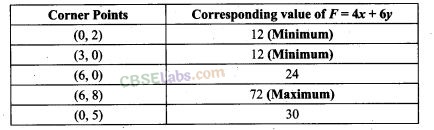
33. Refer to Exercise 32, Maximum of F – Minimum of F=
(a) 60 (b) 48 (c) 42 (d) 18
Sol. (a) Referring to the solution 32, maximum,of F-minimum of F= 72- 12 = 60
34. Comer points of the feasible region determined by the system of linear constraints are (0, 3), (1, 1) and (3, 0). Let Z = px + qy, where p,q>0. Condition on p and q so that the minimum of Z occurs at (3, 0) and (1,1) is
(a) p = 2q (b )P=q\2 (c)p = 3q (d) p = q
Sol. (b)

Fill in the Blanks Type Questions
35. In a LPP, the linear inequalities or restrictions on the variables are called————-.
Sol. In a LPP, the linear inequalities or restrictions on the variables are called linear constraints.
36. In a LPP, the objective function is always————.
Sol. In a LPP, objective function is always linear.
37. If the feasible region for a LPP is————, then the optimal value of the objective function Z= axH-fiy may or may not exist.
Sol. If the feasible region for a LPP is unbounded, then the optimal value of the objective function Z = ax + by may or may not exist.
38. In a LPP if the objective function Z=ax+ by has the same maximum value on two comer points of the feasible region, then every point on the line segment joining these two points give the same————value.
Sol. In a LPP, if the objective function Z = ax + by has the same maximum value on two comer points of the feasible region, then every point on the line segment joining these two points gives the same maximum value.
39. A feasible region of a system of linear inequalities is said to be————if it can be enclosed within a circle.
Sol. A feasible region of a system of linear inequalities is said to be bounded, if it can be enclosed within a circle.
40. A comer point of a feasible region is a point in the region which is the———— of two boundary lines.
Sol. A comer point of a feasible region is a point in the region which is the intersection of two boundary lines.
41. The feasible region for an LPP is always a————polygon.
Sol. The feasible region for an LPP is always a convex polygon.
True/False Type Questions
42. If the feasible region for a LPP is unbounded, maximum or minimum of the objective function Z = ax+ by may or may not exist.
Sol. True
43. Maximum value of the objective function Z = ax+ by in a LPP always occurs
at only one comer point of the feasible region. ,
Sol. False
44. In a LPP, the minimum value of the objective function Z = ax+ by is always 0 if origin is one of the comer point of the feasible region.
Sol. False
45. In a LPP, the maximum value of the objective function Z = ax+ by is always finite.
Sol. True
NCERT Exemplar Class 12 Maths Solutions
- Chapter 1 Relations and Functions
- Chapter 2 Inverse Trigonometric Functions
- Chapter 3 Matrices
- Chapter 4 Determinants
- Chapter 5 Continuity and Differentiability
- Chapter 6 Application of Derivatives
- Chapter 7 Integrals
- Chapter 8 Applications of Integrals
- Chapter 9 Differential Equations
- Chapter 10 Vector Algebra
- Chapter 11 Three Dimensional Geometry
- Chapter 12 Linear Programming
- Chapter 13 Probability
More Resources for Class 12 Maths
- NCERT Exemplar
- NCERT Exemplar Class 12 Maths Solutions
- Class 12 Maths NCERT Solutions
- RD Sharma Class 12 Solutions
- Class 12 Maths Important Questions
We hope the NCERT Exemplar Class 12 Maths Chapter 12 Linear Programming help you. If you have any query regarding NCERT Exemplar Class 12 Maths Chapter 12 Linear Programming, drop a comment below and we will get back to you at the earliest.