A Relation is an Important Concept in Set Theory. Sets, Relations, and Functions are all interlinked. Relations define the Operations Performed on Sets. You can know the connection between given sets using Relations. Get to know about various types of Relations, Representation of Relations in Different Forms, etc. in detail.
- Relations and Mapping
- Ordered Pair
- Cartesian Product of Two Sets
- Domain and Range of a Relation
- Practice Test on Math Relation
- Functions or Mapping
- Domain Co-domain and Range of Function
- Math Practice Test on Functions
Relation Definition
A Relation in math defines the relationship between two different sets of information. If there are two sets then the relation between them is built if there is a connection between elements of two or more non-empty sets.
Types of Relations
There are 8 major types of Relations. We have listed the definitions of each relation along with a Solved Example in the coming modules.
- Empty Relation
- Universal Relation
- Identity Relation
- Inverse Relation
- Reflexive Relation
- Symmetric Relation
- Transitive Relation
- Equivalence Relation
Empty Relation:
In Empty Relation, there will be no relation between any elements of the set. It is also known as Empty Relation and is denoted by R = φ ⊂ A × A
Universal Relation:
In the case of a Universal Relation, every element of the set is associated with each other. Let us assume a set A = { a, b, c}. Universal Relation is given by R = {x, y} where |x – y| ≥ 0. For Universal Relation R = AxA.
Identity Relation:
Every element of a set is related to itself. Consider the Set A = {a, b, c} then Identity Relation is given by I = {a, a}, {b, b}, {c, c}. Identity Relation is given by I = {(a, a), a ∈ A}.
Inverse Relation:
If a set has elements that are inverse pairs of another set then they are said to be in Inverse Relation. If Set A = {(u, v), (w,x)} then inverse relation R-1 = {(v, u), (x, w)}. For an inverse relation R-1 = {(b, a): (a, b) ∈ R}.
Reflexive Relation:
Every element mapped to itself is called a Reflexive Relation. Consider a Set A = {3, 4} then reflexive relation is given by R = {(3,3), (4, 4) (3, 4), (4, 3)}. In general, Reflexive Relation is denoted by (a, a) ∈ R.
Symmetric Relation:
If a= b is true, then b = a is also true in the case of a Symmetric Relation. You can say that a Relation is Symmetric if (a, b) ∈ R is true then (b, a) ∈ R is true. Symmetric Relation is denoted by
aRb ⇒ bRa, ∀ a, b ∈ A
Transitive Relation:
A Relation is said to be transitive if (x, y) ∈ R, (y, z) ∈ R, then (x, z) ∈ R. Transitive Relation is denoted by aRb and bRc ⇒ aRc ∀ a, b, c ∈ A
Equivalence Relation:
If a Relation is Transitive, Symmetric and Reflexive at the Same Time is Known as Equivalence Relation.
Representation of Relation
The relationship between Set A to Set B can be expressed in different forms and they are as under
- Roster Form
- Set Builder Form
- Arrow Diagram
Roster Form: In this form, the relation from one set to the other set is expressed using the ordered pairs. Consider two sets A and B then the first component in each ordered pair is from Set A whereas the second component is from Set B. Remember the Relation dealing with is (>, <, etc.)
Example
If A ={x, y, z} B = {4, 5, 6}
then R = {(x, 4), ((y,5), (z,6)}
Thus, R ⊆ A × B.
Set Builder Form: In the Set Builder Form relation between Set A and Set B is given by R = {(a, b): a ∈ A, b ∈ B, a…b} where blank space denotes the rule that associates a and b.
Example
Let A = { 2, 3, 4, 5, 6} B = { 6, 7, 8, 9} then R = {(2,6), (3, 7), (4,8), (5, 9)}. Here R is in the Set Builder Form in which R = {a, b} : a ∈ A, b ∈ B, a is 4 less than b.
Arrow Diagram:
- Draw two circles denoting Set A and Set B.
- Note down the corresponding elements of the Set A in Circle A and elements of the Set B in the Circle B.
- Draw Arrows from A to B that satisfy the relation and indicate the ordered pairs too.
Example:
If A = {1, 2, 3} and B ={5, 7, 9} then Relation R from Set A to Set B is denoted by the arrow diagram as such
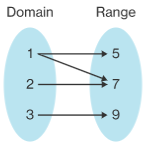
Here R = {(1,5), (1,7), (2, 7), (3, 9)}
Relation from Set A to Set B is shown by drawing arrows from the 1st components to the 2nd components of all ordered pairs that belong to R.