RD Sharma Class 10 Solutions Chapter 14 Coordinate Geometry Ex 14.3

RD Sharma Class 10 Solutions Chapter 14 Coordinate Geometry Ex 14.3

RD Sharma Class 10 Solutions Co-Ordinate Geometry Exercise 14.3

Question 1.
Find the coordinates of the point which divides the line segment joining (-1, 3) and (4, -7) internally in the ratio 3 : 4.
Solution:
The line segment joining the points A (-1,3) and B (4, -7) is divided into the ratio 3 : 4
Let P (x, y) divides AB in the ratio 3 : 4

Question 2.
Find the points of trisection of the line segment joining the points :
(i) (5, -6) and (-7, 5)
(ii) (3, -2) and (-3, -4)
(iii) (2, -2) and (-7, 4) [NCERT]
Solution:
(i) The line segment whose end points are A (5, -6) and B (-7,5) which is trisected at C and D
C divides it in the ratio 1 : 2
i.e., AC : CB = 1 : 2

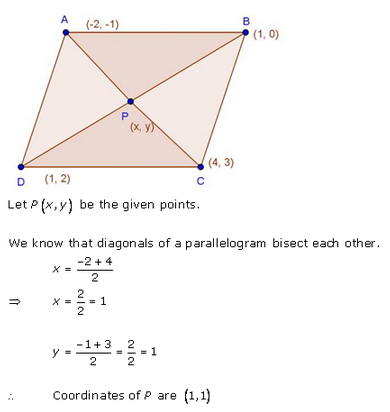
Question 3.
Find the coordinates of the point where the diagonals of the parallelogram formed by joining the points (-2, -1), (1, 0) (4,3) and (1, 2) meet.
Solution:
Let the vertices of the parallelogram ABCD be A (-2, -1), B (1, 0), C (4, 3) and D (1, 2) in which AC and BD are its diagonals which bisect each other at O

Question 4.
Prove that the points (3, -2), (4, 0), (6, -3) and (5, -5) are the vertices of a parallelogram.
Solution:
Let the vertices of the quadrilateral ABCD be A (3, -2), B (4, 0), C (6, -3) and D (5, -5)
Now co-ordinates of the mid-point of AC

Question 5.
If P (9a – 2, -b) divides the line segment joining A (3a + 1, -3) and B (8a, 5) in the ratio 3 : 1, find the values of a and b. [NCERT Exemplar]
Solution:
Let P (9a – 2, -b) divides AB internally in the ratio 3 : 1.
By section formula,

=> 9a – 9 = 0
a = 1

Question 6.
If (a, b) is the mid-point of the line segment joining the points A (10, -6), B (k, 4) and a – 2b = 18, find the value of k and the distance AB. [NCERT Exemplar]
Solution:
Since, (a, b) is the mid-point of line segment AB.

Question 7.
Find the ratio in which the points (2, y) divides the line segment joining the points A (-2, 2) and B (3, 7). Also, find the value of y. (C.B.S.E. 2009)
Solution:
Let the point P (2, y) divides the line segment joining the points A (-2, 2) and B (3, 7) in the ratio m₁ : m₂

Question 8.
If A (-1, 3), B (1, -1) and C (5, 1) are the vertices of a triangle ABC, find the length of the median through A.
Solution:
In ∆ABC, the vertices are A (-1, 3), B (1, -1) and C (5, 1)
D is the mid-point of BC
Co-ordinates of D will be (\(\frac { 1 + 5 }{ 2 }\) , \(\frac { -1 + 1 }{ 2 }\))

Question 9.
If the points P, Q (x, 7), R, S (6, y) in this order divide the line segment joining A (2, p) and B (7,10) in 5 equal parts, find x, y and p. [CBSE 2015]
Solution:
Points P, Q (x, 7), R, S (6, y) in order divides a line segment joining A (2, p) and B (7, 10) in 5 equal parts
i.e., AP = PQ = QR = RS = SB
Q is the mid point of A and S

Question 10.
If a vertex of a triangle be (1, 1) and the middle points of the sides through it be (-2, 3) and (5, 2), find the other vertices.
Solution:
Let co-ordinates of one vertex A are (1, 1) and mid-points of AB and AC are D (-2, 3) and E (5, 2)
Let the co-ordinates of B be (x₁, y₁) and C be (x₂, y₂)

Question 11.
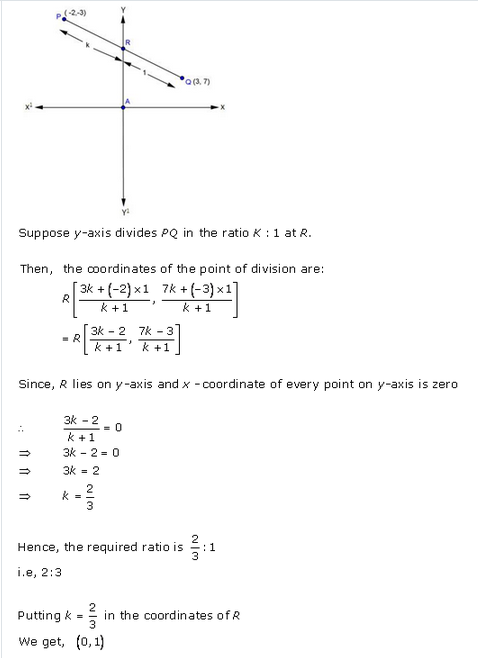
(i) In what ratio is the line segment joining the points (-2, -3) and (3, 7) divided by the y-axis ? Also find the co-ordinates of the point of division. [CBSE 2006C]
(ii) In what ratio is the line segment joining (-3, -1) and (-8, -9) divided at the point (-5, \(\frac { -21 }{ 5 }\)) ?
Solution:
(i) The point lies on y-axis
Its abscissa is O
Let the point (0, y) intersects the line joining the points (-2, -3) and (3, 7) in the ratio m : n

Question 12.
If the mid-point of the line joining (3, 4) and (k, 7) is (x, y) and 2x + 2y + 1 = 0, find the value of k.
Solution:
Mid-point of the line joining the points (3, 4) and (k, 7) is (x, y)

Question 13.
Find the ratio in which the points P (\(\frac { 3 }{ 4 }\) , \(\frac { 5 }{ 12 }\)) divides the line segments joining the points A (\(\frac { 1 }{ 2 }\) , \(\frac { 3 }{ 2 }\)) and B (2, -5). [CBSE 2015]
Solution:

Question 14.
Find the ratio in which the line segment joining (-2, -3) and (5, 6) is divided by (i) x-axis (ii) y-axis. Also, find the co-ordinates of the point of division in each case.
Solution:
(i) Ordinate of a point on x-axis is zero
Let the co-ordinate of the point on x-axis be (0, x)
But (x, 0) is a point which divides the line segment joining the points (-2, -3) and (5, 6) in the ratio m : n

Question 15.
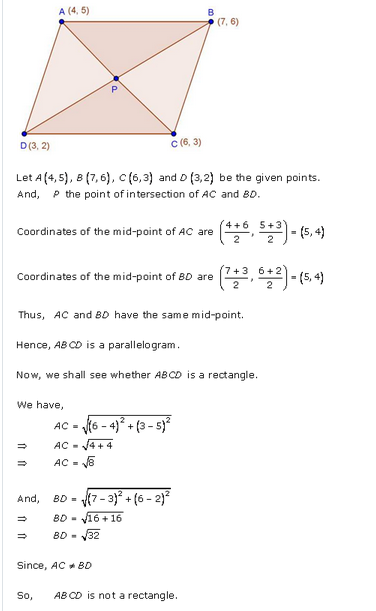
Prove that the points (4, 5), (7, 6), (6, 3), (3, 2) are the vertices of a parallelogram. Is it a rectangle ?
Solution:
The vertices of a parallelogram ABCD are A (4, 5), B (7, 6), C (6, 3), and D (3, 2)
The diagonals AC and BD bisect each other at O
O is the mid-point of AC as well as of BD

Question 16.
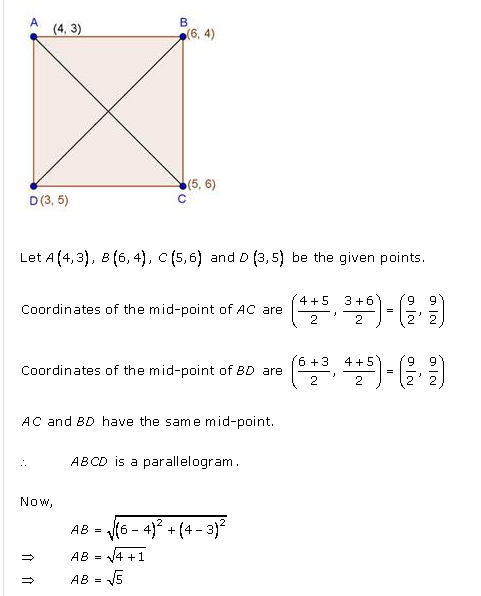
Prove that (4, 3), (6, 4), (5, 6) and (3, 5) are the angular points of a square.
Solution:
Let A (4, 3), B (6, 4), C (5, 6) and D (3, 5) are the vertices of a square ABCD.
AC and BD are its diagonals which bisects each other at O.
O is the mid-point of AC


The diagonals of the quadrilateral ABCD are equal and bisect eachother at O and sides are equal
ABCD is a square

Question 17.
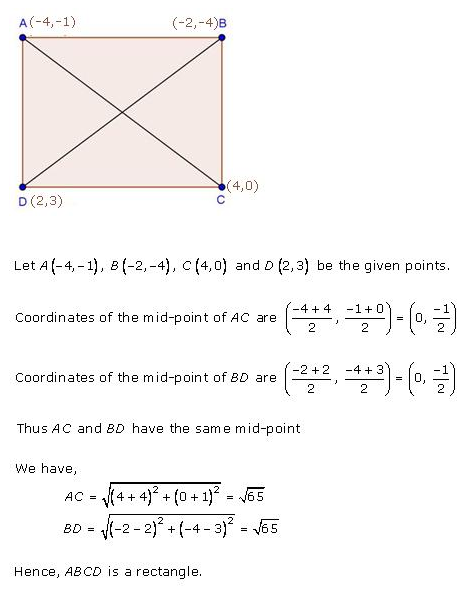
Prove that the points (-4, -1), (-2, -4), (4, 0) and (2, 3) are the vertices of a rectangle.
Solution:
Let the vertices of a quadrilateral ABCD are A (-4, -1), B (-2, -4), C (4, 0) and D (2, 3)
Join AC and BD which intersect eachother at O
If O is the mid-point of AC then its co

Question 18.
Find the lengths of the medians of a triangle whose vertices are A (-1, 3), B (1, -1) and C (5, 1).
Solution:
The co-ordinates of the vertices of ∆ABC are A (-1, 3), B (1, -1) and C (5, 1)
D, E and F are the mid-points of sides BC, CA and AB respectively

Question 19.
Find the ratio in which the line segment joining the pionts A (3, -3) and B (-2, 7) is divided by x-axis. Also, find the coordinates of the point of division. [CBSE 2014]
Solution:
Let a point P (x, 0)
x-axis divides the line segment joining the points A (3, -3) and B (-2, 7) in the ratio m₁ : m₂

Question 20.
Find the ratio in which the point P (x, 2) divides the line segment joining the points A (12, 5) and B (4, -3). Also, find the value of x. [CBSE 2014]
Solution:
Let P (x, 2) divides the line segment joining the points A (12, 5) and B (4, -3) in the ratio m₁ : m₂

Question 21.
Find the ratio in which the point P (-1, y) lying on the line segment joining A (-3, 10) and B (6, -8) divides it. Also find the value of y.
Solution:

Question 22.
Find the coordinates of a point A, where AB is a diameter of the circle whose centre is (2, -3) and B is (1, 4).
Solution:
AB is the diameter of the circle and O is the centre of the circle

Question 23.
If the points (-2, -1), (1, 0), (x, 3) and (1, y) form a parallelogram, find the values of x and y.
Solution:
In ||gm ABCD, co-ordinates of A (-2, -1), B (1, 0),C(x, 3) and D(1, y)
AC and BD are its diagonals which bisect eachother at O

x = 4, y = 2

Question 24.
The points A (2, 0), B (9, 1), C (11, 6) and D (4, 4) are the vertices of a quadrilateral ABCD. Determine whether ABCD is a rhombus or not.
Solution:
The co-ordinates of vertices of a quadrilateral ABCD are A (2,0), B (9,1), C (11,6) and D (4, 4)
AC and BD are its diagonals which intersect eachother at O

The co-ordinates of O in both cases are not same.
It is not a parallelogram and also not a rhombus.

Question 25.
In what ratio does the point (-4, 6) divide the line segment joining the points A (-6, 10) and B (3, -8) ?
Solution:
Let the point P (-4, 6) divides the line segment joining the points A (-6, 10) and B (3, -8) in the ratio m₁ : m₂

Question 26.
Find the ratio in which the y-axis divides the line segment joining the points (5, -6) and (-1, -4). Also, find the coordinates of the point of division.
Solution:
The points lies on y-axis
Let its coordinates be (0, y)
and let it divides the line segment joining the points (5, -6) and (-1, -4) in the ratio m₁ : m₂

Question 27.
Show that A (-3, 2), B (-5, -5), C (2, -3) and D (4, 4) are the vertices of a rhombus.
Solution:
Vertices of a quadrilateral ABCD are A (-3, 2), B (-5, -5), C (2, -3) and D (4, 4)
Join the diagonals AC and BD which intersect each other at O

Question 28.
Find the lengths of the medians of a ∆ABC having vertices A (0, -1), B (2, 1) and C (0, 3).
Solution:
A (0, -1), B (2, 1) and C (0, 3) are the vertices of ∆ABC
Let D, E and F are the mid points of BC, CA and AB respectively

Question 29.
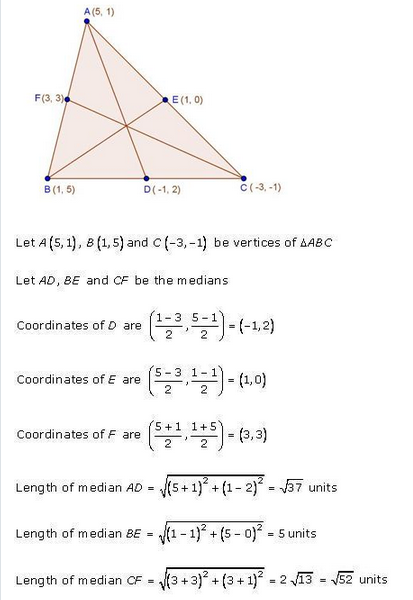
Find the lengths of the medians of a ∆ABC, having the vertices at A (5, 1), B (1, 5) and C (3,-1).
Solution:
A (5, 1), B (1, 5) and C (3, -1) are the vertices of ∆ABC

Question 30.
Find the co-ordinates of the points which divide the line segment joining the points (-4, 0) and (0, 6) in four equal parts.
Solution:
AB is a line segment whose ends points are A (-4, 0) and B (0, 6)

Question 31.
Show that the mid-point of the line segment joining the points (5, 7) and (3, 9) is also the mid-point of the line segment joining the points (8, 6) and (0, 10).
Solution:
Let M be the mid point of AB. Co-ordinates of the mid point of this line segment joining two points A (5, 7) and B (3, 9)

Question 32.
Find the distance of the point (1, 2) from the mid-point of the line segment joining the points (6, 8) and (2, 4).
Solution:
Let M be the mid-point of the line segment joining the points (6, 8) and (2, 4)
Now co-ordinates of M will be

Question 33.
If A and B are (1, 4) and (5, 2) respectively, find the co-ordinates of P When \(\frac { AP }{ BP }\) = \(\frac { 3 }{ 4 }\)
Solution:
Point P divides the line segment joining the points (1, 4) and (5, 2) in the ratio of AP : PB = 3 : 4
Co-ordinates of P will be

Question 34.
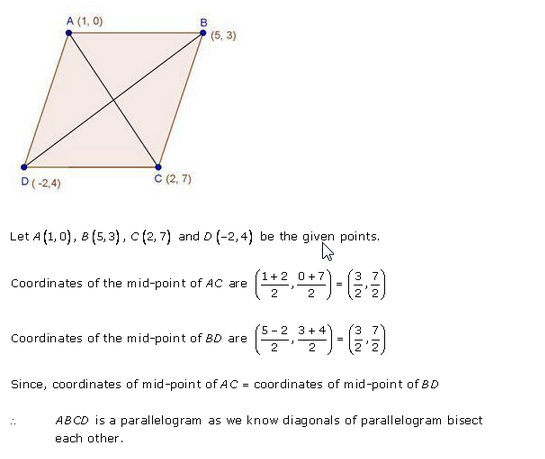
Show that the points A (1, 0), B (5, 3), C (2, 7) and D (-2, 4) are the vertices of a parallelogram.
Solution:
If ABCD is a parallelogram, then its diagonal
AC and BD bisect eachother at O
Let O is the mid-point of AC, then co

Question 35.
Determine the ratio in which the point P (m, 6) divides the join of A (-4, 3) and B (2, 8). Also find the value of m. [CBSE 2004]
Solution:
Let the ratio be r : s in which P (m, 6) divides the line segment joining the points A (-4, 3) and B (2, 8)

Question 36.
Determine the ratio in which the point (-6, a) divides the join of A (-3, -1) and B (-8, 9). Also find the value of a. [CBSE 2004]
Solution:
Let the point P (-6, a) divides the join of A (-3, -1) and B (-8, 9) in the ratio m : n

Question 37.
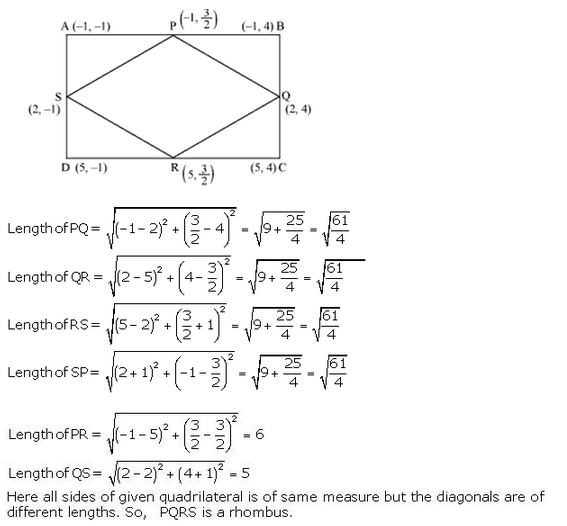
ABCD is a rectangle formed by joining the points A (-1, -1), B (-1, 4), C (5, 4) and D (5, -1). P, Q, R and S are the mid-points of sides AB, BC, CD and DA respectively. Is the quadrilateral PQRS a square ? a rectangle ? or a rhombus ? Justify your answer.
Solution:
ABCD is a rectangle whose vertices are A (-1,-1), B (-1,4), C (5, 4) and D (5, -1) P, Q, R, and S are the mid-points of the sides AB, BC, CD and DA respectively and are joined PR and QS are also joined.

Question 38.
Points P, Q, R and S divide the line segment joining the pionts A (1, 2) and B (6, 7) in 5 equal parts. Find the coordinates of the points P, Q and R. [CBSE 2014]
Solution:
Points P, Q, R and S divides AB in 5 equal parts and let coordinates of P, Q, R and S be

Coordinates of R are (4, 5)

Question 39.
If A and B are two points having co-ordinates (-2, -2) and (2, -4) respectively, find the co-ordinates of P such that AP = \(\frac { 3 }{ 7 }\) AB
Solution:

Question 40.
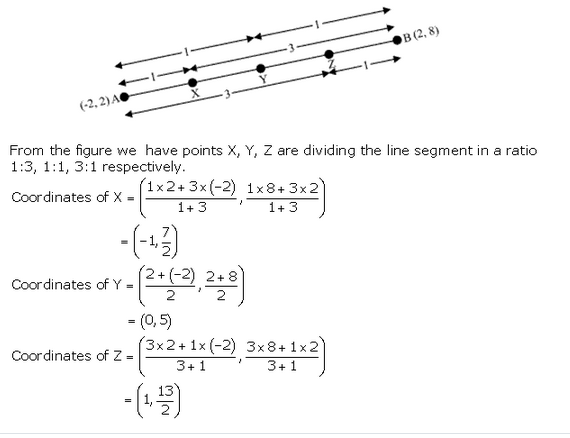
Find the co-ordinates of the points which divide the line segment joining A (-2, 2) and B (2, 8) into four equal parts.
Solution:
Let P, Q and R divides the line segment AB in four equal parts
Co-ordinates of A are (-2, 2) and of B are (2, 8)

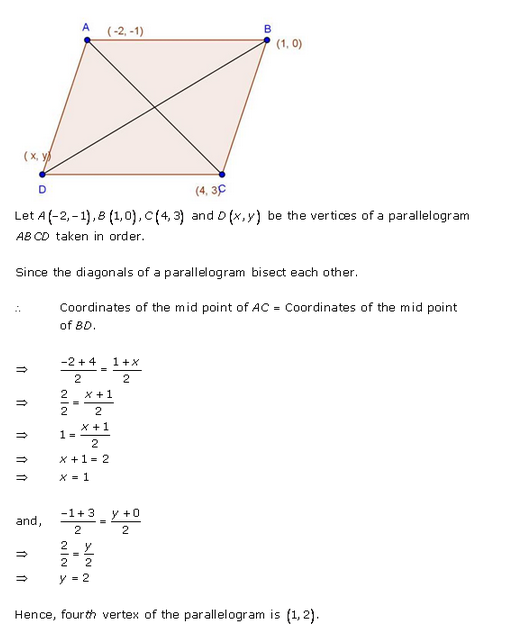
Question 41.
Three consecutive vertices of a parallelogram are (-2, -1), (1, 0) and (4, 3). Find the fourth vertex.
Solution:
Let the co-ordinates of three vertices are A (-2, -1), B (1, 0) and C (4, 3)
and let the diagonals AC and BD bisect each other at O

and \(\frac { y }{ 2 }\) = 1 => y = 2
Co-ordinates of D will be (1, 2)

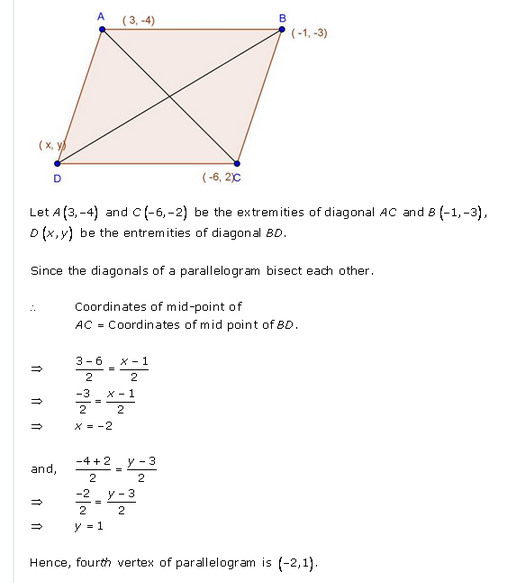
Question 42.
The points (3, -4) and (-6, 2) are the extremities of a diagonal of a parallelogram. If the third vertex is (-1, -3). Find the co-ordinates of the fourth vertex.
Solution:
Let the extremities of a diagonal AC of a parallelogram ABCD are A (3, -4) and C (-6, 2)
Let AC and BD bisect eachother at O

Question 43.
If the co-ordinates of the mid-points of the sides of a triangle are (1, 1), (2, -3) and (3, 4), find the vertices of the triangle.
Solution:
Let A (x₁, y₁), B (x₂, y₂) and C (x₃, y₃) be the vertices of the ∆ABC
D, E and F are the mid-points of BC, CA and AB respectively such that their co-ordinates are D (1, 1), E (2, -3) and F (3, 4)
D is mid-point of BC

Question 44.
Determine the ratio in which the straight line x – y – 2 = 0 divides the line segment joining (3, -1) and (8, 9).
Solution:
Let the straight line x – y – 2 = 0 divides the line segment joining the points (3, -1), (8, 9) in the ratio m : n
Co-ordinates of the point will be

Question 45.
Three vertices of a parallelogram are (a + b, a – b), (2 a + b, 2a – b), (a – b, a + b). Find the fourth vertex.
Solution:
In parallelogram ABCD co-ordinates are of A (a + b, a – b), B (2a + b, 2a – b), C (a – b, a + b)
Let co-ordinates of D be (x, y)
Join diagonal AC and BD
Which bisect eachother at O
O is the mid-point of AC as well as BD

Question 46.
If two vertices of a parallelogram are (3, 2), (-1, 0) and the diagonals cut at (2, -5), find the other vertices of the parallelogram.
Solution:
Two vertices of a parallelogram ABCD are A (3,2), and B (-1, 0) and its diagonals bisect each other at O (2, -5)

Question 47.
If the co-ordinates of the mid-points of the sides of a triangle ar6 (3, 4), (4, 6) and (5, 7), find its vertices. [CBSE 2008]
Solution:
The co-ordinates of the mid-points of the sides BC, CA and AB are D (3, 4), E (4, 6) and F (5, 7) of the ∆ABC

Question 48.
The line segment joining the points P (3, 3) and Q (6, -6) is trisected at the points A and B such that A is nearer to P. If A also lies on the line given by 2x + y + k = 0, find the value of k. [CBSE 2009]
Solution:
Two points A and B trisect the line segment joining the points P (3, 3) and Q (6, -6) and A is nearer to P
and A lies also on the line 2x + y + k = 0

=> k = -8
Hence k = -8

Question 49.
If three consecutive vertices of a parallelogram are (1, -2), (3, 6) and (5, 10), find its fourth vertex.
Solution:
A (1, -2), B (3, 6) and C (5, 10) are the three consecutive vertices of the parallelogram ABCD
Let (x, y) be its fourth vertex
AC and BD are its diagonals which bisect each other at O

Question 50.
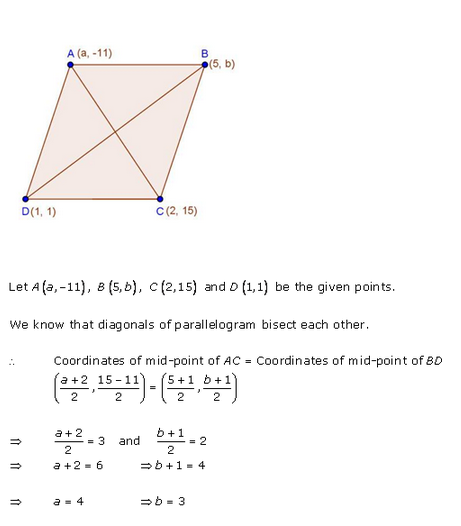
If the points A (a, -11), B (5, b), C (2, 15) and D (1, 1) are the vertices of a parallelogram ABCD, find the values of a and b.
Solution:
A (a, -11), B (5, b), C (2, 15) and D (1, 1) are the vertices of a parallelogram ABCD
Diagonals AC and BD bisect eachother at O

Question 51.
If the co-ordinates of the mid-points of the sides of a triangle be (3, -2), (-3, 1) and (4, -3), then find the co-ordinates of its vertices.
Solution:
In a ∆ABC,
D, E and F are the mid-points of the sides BC, CA and AB respectively and co-ordinates of D, E and F are (3, -2), (-3, 1) and (4, -3) respectively

Question 52.
The line segment joining the points (3, -4) and (1, 2) is trisected at the points P and Q. If the co-ordinates of P and Q are (p, -2) and (\(\frac { 5 }{ 3 }\) , q) respectively, find the values of p and q. [CBSE 2005]
Solution:

Question 53.
The line joining the points'(2, 1), (5, -8) is trisected at the points P and Q. If point P lies on the line 2x – y + k = 0, find the value of k. [CBSE 2005]
Solution:
Points A (2, 1), and B (5, -8) are the ends points of the line segment AB

Question 54.
A (4, 2), B (6, 5) and C (1, 4) are the vertices of ∆ABC,
(i) The median from A meets BC in D. Find the coordinates of the point D.
(ii) Find the coordinates of point P on AD such that AP : PD = 2 : 1.
(iii) Find the coordinates of the points Q and R on medians BE and CF respectively such that BQ : QE = 2 : 1 and CR : RF = 2 : 1.
(iv) What do you observe? [NCERT,CBSE, 2009, 10]
Solution:
In ∆ABC, co-ordinates of A (4, 2) of (6, 5) and of (1, 4) and AD is BE and CF are the medians such that D, E and F are the mid points of the sides BC, CA and AB respectively
P is a point on AD such that AP : PD = 2 : 1




(iv) We see that co-ordinates of P, Q and R are same i.e., P, Q and R coincides eachother. Medians of the sides of a triangle pass through the same point which is called the centroid of the triangle.

Question 55.
If the points A (6, 1), B (8, 2), C (9, 4) and D (k, p) are the vertices of a parallelogram taken in order, then find the values of k and p.
Solution:
The diagonals of a parallelogram bisect each other
O is the mid-point of AC and also of BD
O is the mid-point of AC

Question 56.
A point P divides the line segment joining the points A (3, -5) and B (-4, 8) such that \(\frac { AP }{ PB }\) = \(\frac { k }{ 1 }\). If P lies on the line x + y = 0, then find the value of k. [CBSE 2012]
Solution:
Point P divides the line segment by joining the points A (3, -5) and B (-4, 8)

Question 57.
The mid-point P of the line segment joining the points A (-10, 4) and B (-2, 0) lies on the line segment joining the pionts C (-9, -4) and D (-4, y). Find the ratio in which P divides CD. Also, find the value of y. [CBSE 2014]
Solution:
P is the mid-point of line segment joining the points A (-10, 4) and B (-2, 0)
Coordinates of P will be

=> y = \(\frac { 18 }{ 3 }\) = 6
y = 6

Question 58.
If the point C (-1, 2) divides internally the line segment joining the points A (2, 5) and B (x, y) in the ratio 3 : 4, find the value of x² + y². [CBSE 2016]
Solution:

Question 59.
ABCD is a parallelogram with vertices A (x₁, y₁), B (x₂, y₂) and C (x₃, y₃). Find the coordinates of the fourth vertex D in terms of x₁, x₂, x₃, y₁, y₂ and y₃. [NCERT Exemplar]
Solution:
Let the coordinates of D be (x, y). We know that diagonals of a parallelogram bisect each other.

Question 60.
The points A (x₁, y₁), B (x₂, y₂) and C (x₃, y₃) are the vertices of ∆ABC.
(i) The median from A meets BC at D. Find the coordinates of the point D.
(ii) Find the coordinates of the point P on AD such that AP : PD = 2 : 1.
(iii) Find the points of coordinates Q and R on medians BE and CF respectively such that BQ : QE = 2 : 1 and CR : RF = 2 : 1.
(iv) What are the coordinates of the centroid of the triangle ABC? [NCERT Exemplar]
Solution:
Given that, the points A (x₁, y₁), B (x₂, y₂) and C (x₃, y₃) are the vertices of ∆ABC.
(i) We know that, the median bisect the line segment into two equal parts i.e., here D is the mid-point of BC.

RD Sharma Class 10 Solutions Chapter 14 Coordinate Geometry Ex 14.3 Q1

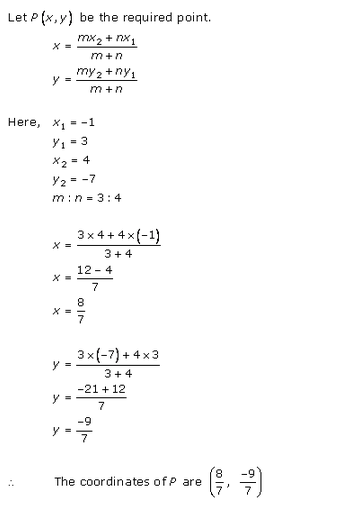
RD Sharma Class 10 Solutions Chapter 14 Coordinate Geometry Ex 14.3 Q2


RD Sharma Class 10 Solutions Chapter 14 Coordinate Geometry Ex 14.3 Q3

RD Sharma Class 10 Solutions Chapter 14 Coordinate Geometry Ex 14.3 Q4

Ex 14.3 Q 5

Ex 14.3 Q6

Ex 14.3 Q7

Ex 14.3 Q8

Ex 14.3 Q9

Ex 14.3 Q9 i

Ex 14.3 Q10

Ex 14.3 Q11


Ex 14.3 Q12

Ex 14.3 Q13

Ex 14.3 Q14

RD Sharma Class 10 Solutions Chapter 14 Ex 14.3 Q14 i

RD Sharma Class 10 Solutions Chapter 14 Ex 14.3 Q15

RD Sharma Class 10 Solutions Chapter 14 Ex 14.3 Q16

RD Sharma Class 10 Solutions Chapter 14 Ex 14.3 Q16

RD Sharma Class 10 Solutions Chapter 14 Ex 14.3 Q17

RD Sharma Class 10 Solutions Chapter 14 Ex 14.3 Q18

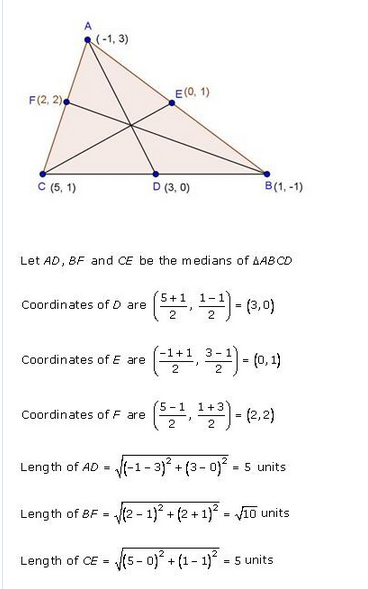
RD Sharma Class 10 Solutions Chapter 14 Ex 14.3 Q19

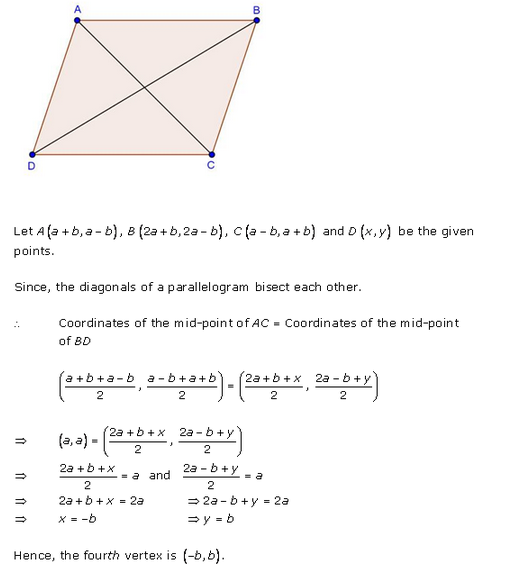
RD Sharma Class 10 Solutions Chapter 14 Ex 14.3 Q20

RD Sharma Class 10 Solutions Chapter 14 Ex 14.3 Q21

RD Sharma Class 10 Solutions Chapter 14 Ex 14.3 Q21

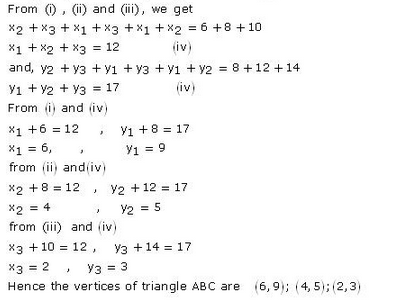
RD Sharma Class 10 Solutions Chapter 14 Ex 14.3 Q22

RD Sharma Class 10 Solutions Chapter 14 Ex 14.3 Q23

RD Sharma Class 10 Solutions Chapter 14 Ex 14.3 Q24

RD Sharma Class 10 Solutions Chapter 14 Ex 14.3 Q25

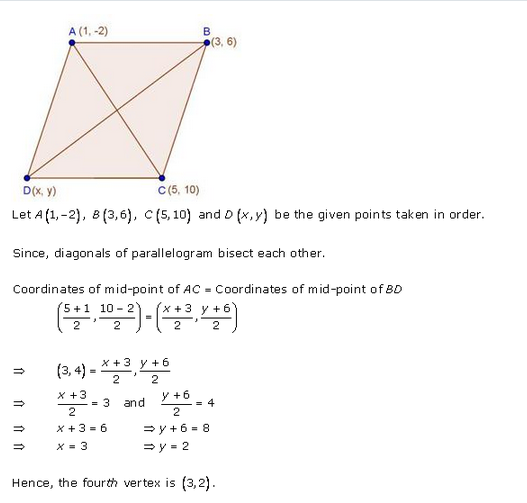
RD Sharma Class 10 Solutions Chapter 14 Ex 14.3 Q26

RD Sharma Class 10 Solutions Chapter 14 Ex 14.3 Q27


RD Sharma Class 10 Solutions Chapter 14 Ex 14.3 Q28

RD Sharma Class 10 Solutions Chapter 14 Ex 14.3 Q29

RD Sharma Class 10 Solutions Chapter 14 Ex 14.3 Q30

RD Sharma Class 10 Solutions Chapter 14 Ex 14.3 Q31

Chapter 14 Ex 14.3 Q32

Chapter 14 Ex 14.3 Q33

Chapter 14 Ex 14.3 Q34

Chapter 14 Ex 14.3 Q35

Chapter 14 Ex 14.3 Q36

Chapter 14 Ex 14.3 Q37

38.

39.

40.

41.

42.

43.

44.

45.

46.

47.

48.

RD Sharma Class 10 Solutions

• Chapter 14 Co-Ordinate Geometry Ex 14.1
• Chapter 14 Co-Ordinate Geometry Ex 14.2
• Chapter 14 Co-Ordinate Geometry Ex 14.3
• Chapter 14 Co-Ordinate Geometry Ex 14.4
• Chapter 14 Co-Ordinate Geometry Ex 14.5