RD Sharma Class 10 Solutions Chapter 14 Coordinate Geometry Ex 14.5
RD Sharma Class 10 Solutions Co-Ordinate Geometry Exercise 14.5
Question 1.
Find the area of a triangle whose vertices are :
(i) (6, 3), (-3, 5) and (4, -2)
(ii) (\({ at }_{ 1 }^{ 2 }\), 2at1), (\({ at }_{ 2 }^{ 2 }\), 2at2) and (\({ at }_{ 3 }^{ 2 }\), 2at3)
(iii) (a, c + a), (a, c) and (-a, c – a)
Solution:
(i) Co-ordinates of ∆ABC are A (6, 3), B (-3, 5) and C (4, -2)



Question 2.
Find the area of the quadrilaterals, the coordinates of whose vertices are
(i) (-3, 2), (5, 4), (7, -6) and (-5, -4)
(ii) (1, 2), (6, 2), (5, 3) and (3, 4)
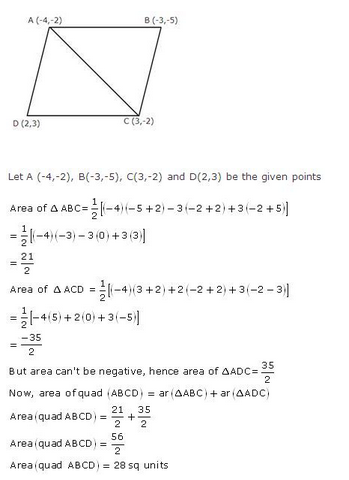
(iii) (-4, -2), (-3, -5), (3, -2), (2, 3) (C.B.S.E. 2009)
Solution:
(i) Let vertices of quadrilateral ABCD be A (-3, 2), B (5, 4), C (7, -6) and D (-5, -4)
Join AC






Question 3.
The four vertices of a quadrilaterals are (1, 2), (-5, 6), (7, -4) and (k, -2) taken in order. If the area of the quadrilateral is zero, find the value of k ?
Solution:
Let the vertices of quadrilateral ABCD be
A (1, 2), B (-5, 6), C (7, -4) and D (k, -2)
Join AC



Question 4.
The vertices of ∆ABC are (-2, 1), (5, 4) and (2, -3) respectively. Find the area of the triangle and the length of the altitude through A.
Solution:
Vertices of ∆ABC are A (-2, 1), B (5, 4) and C (2, -3) and AD ⊥ BC, let AD = h
Now area of ∆ABC


Question 5.
Show that the following sets of points are collinear
(a) (2, 5), (4, 6) and (8, 8)
(b) (1, -1), (2, 1) and (4, 5)
Solution:
We know that points are collinear if the area of the triangle formed by them is zero
(a) Vertices of ∆ABC are (2, 5), (4, 6) and (8, 8)


Question 6.
Find the area of a quadrilateral ABCD, the coordinates of whose varities are A (-3, 2), B (5, 4), C (7, -6) and D (-5, -4). [CBSE 2016]
Solution:
Area of quadrilateral ABCD
= area of ∆ABC + area of ∆ACD

Question 7.
In ∆ABC, the coordinates of vertex A are (0, -1) and D (1, 0) and E (0, 1) respectively the mid-points of the sides AB and AC. If F is the mid-point of side C, find the area of ∆DEF. [CBSE 2016]
Solution:
Let B (p, q), C (r, s) and F (x, y)
Mid-point of AB = Coordinates of D



Question 8.
Find the area of the triangle PQR with Q (3, 2) and the mid-points of the sides through Q being (2, -1) and (1, 2). [CBSE 2015]
Solution:
In ∆PQR, L and N are mid points of QR and QP respectively coordinates of Q are (3, 2) of L are (2, -1) and of N are (1, 2)


Question 9.
If P (-5, -3), Q (-4, -6), R (2, -3) and S (1, 2) are the vertices of a quadrilateral PQRS, find its area. [CBSE 2015]
Solution:
P (-5, -3), Q (-4, -6), R (2, -3) and S (1,2) are the vertices of a quadrilateral PQRS
Join PR which forms two triangles PQR and PSR


Question 10.
If A (-3, 5), B (-2, -7), C (1, -8) and D (6, 3) are the vertices of a quadrilateral ABCD, find its area. [CBSE 2014]
Solution:
A (-3, 5), B (-2, -7), C (1,-8) and D (6, 3) are the vertices of a quadrilateral ABCD
Join AC


Question 11.
For what value of ‘a’ the points (a, 1), (1, -1) and (11, 4) are collinear ?
Solution:
Let the vertices of ∆ABC are A (a, 1), B (1, -1) and C (11, 4)

Question 12.
Prove that the points (a, b), (a1, b1) and (a – a1, b – b1) are collinear if ab1 = a1b.
Solution:

Question 13.
If the vertices of a triangle are (1, -3), (4, p) and (-9, 7) and its area is 15 sq. units, find the value(s) of p. [CBSE 2012]
Solution:
The vertices of a triangle are (1, -3), (4, p) and (-9, 7) and area of triangle = 15 sq. units


Question 14.
If (x, y) be on the line joining the two points (1, -3) and (-4, 2), prove that x + y + 2 = 0.
Solution:
Point (x, y) be on the line joining the two points (1, -3) and (-4, 2)
Points (x, y), (1, -3) and (-4, 2) are collinear
Let the points (x, y) (1, -3) and (-4, 2) are the vertices of a triangle, then

Question 15.
Find the value of k if points (k, 3), (6, -2) and (-3, 4) are collinear. [CBSE 2008]
Solution:
Let the points (k, 3), (6, -2) and (-3, 4) be the vertices of a triangle, then


Question 16.
Find the value of k, if the points A (7, -2), B (5, 1) and C (3, 2k) are collinear. [CBSE 2010]
Solution:
Points A (7, -2), B (5, 1) and C (3, 2k) are collinear
area of ∆ABC = 0

Question 17.
If the point P (m, 3) lies on the line segment joining the points A (\(\frac { -2 }{ 5 }\) , 6) and B (2, 8), find the value of m.
Solution:

Question 18.
If R (x, y) is a point on the line segment joining the points P (a, b) and Q (b, a), then prove that x + y = a + b. [CBSE 2010]
Solution:
Point R (x, y) lies on the line segment joining the points P (a, b) and Q (b, a)
Area of ∆PRQ = 0


Question 19.
Find the value of k, if the points A (8, 1), B (3, -4) and C (2, k) are collinear. [CBSE 2010]
Solution:
The points A (8, 1), B (3, -4) and C (2, k) are collinear
Area of ∆ABC = 0

Question 20.
Find the value of a for which the area of the triangle formed by the points A (a, 2a), B (-2, 6) and C (3, 1) is 10 square units.
Solution:

Question 21.
If a ≠ b ≠ 0, prove that the points (a, a²), (b, b²), (0, 0) are never collinear. [CBSE 2017]
Solution:


Question 22.
The area of a triangle is 5 sq. units. Two of its vertices are at (2, 1) and (3, -2). If the third vertex is (\(\frac { 7 }{ 2 }\) , y), find y. [CBSE 2017]
Solution:

Question 23.
Prove that the points (a, 0), (0, b) and (1, 1) are collinear if, \(\frac { 1 }{ a }\) + \(\frac { 1 }{ b }\) = 1.
Solution:
Let the points are A (a, 0), B (0, b) and C (1, 1) which form a triangle

Question 24.
The point A divides the join of P (-5, 1) and Q (3, 5) in the ratio k : 1. Find the two values of k for which the area of ∆ABC where B is (1, 5) and C (7, -2) is equal to 2 units.
Solution:
Let the coordinates of A be (x, y) which divides the join of P (-5, 1) and Q (3, 5) in the ratio. Then



Question 25.
The area of a triangle is 5. Two of its vertices are (2, 1) and (3, -2). The third vertex lies on y = x + 3. Find the third vertex.
Solution:
Let the coordinates of third vertex of the triangle be (x, y) and other two vertices are (2, 1) and (3, 2)


Question 26.
If a ≠ b ≠ c, prove that the points (a, a²), (b, b²), (c, c²) can never be collinear.
Solution:


Question 27.
Four points A (6, 3), B (-3, 5), C (4, -2) and D (x, 3x) are given in such a way that \(\frac { \triangle DBC }{ \triangle ABC } =\frac { 1 }{ 2 }\) , find x?
Solution:
Let A (6, 3), B (-3, 5), C (4, -2) and D (x, 3x) are the vertices of quadrilateral ABCD
AC and BD are joined



Question 28.
If three points (x1, y1), (x2, y2), (x3, y3) lie on the same line, prove that

Solution:
Let the points (x1, y1), (x2, y2), (x3, y3) are the vertices of a triangle

Question 29.
Find the area of a parallelogram ABCD if three of its vertices are A (2, 4), B (2 + √3, 5) and C (2, 6). [CBSE 2013]
Solution:
Three vertices of a ||gm ABCD are A (2, 4), B (2 + √3 , 5) and C (2, 6).
Draw one diagonal AC of ||gm ABCD


Question 30.
Find the value (s) of k for which the points (3k – 1, k – 2), (k, k – 7) and (k – 1, -k – 2) are collinear. [CBSE 2014]
Solution:

Question 31.
If the points A (-1, -4), B (b, c) and C (5, -1) are collinear and 2b + c = 4, find the values of b and c. [CBSE 2014]
Solution:


Question 32.
If the points A (-2, 1), B (a, b) and C (4, -1) are collinear and a – b = 1, find the values of a and 6. [CBSE 2014]
Solution:
Points A (-2, 1), B (a, b) and C (4, -1) are
collinear if area ∆ABC = 0
Now area of ∆ABC


Question 33.
If the points A (1, -2), B (2, 3), C (a, 2) and D (-4, -3) form a parallelogram, find the value of a and height of the parallelogram taking AB as base. [NCERT Exemplar]
Solution:
In parallelogram, we know that, diagonals bisects each other
i.e., mid-point of AC = mid-point of BD





Question 34.
A (6, 1), B (8, 2) and C (9, 4) are three vertices of a parallelogram ABCD. If E is the mid-point of DC, find the area of ∆ADE. [NCERT Exemplar]
Solution:
Given that, A (6,1), B (8,2) and C (9,4) are three vertices of a parallelogram ABCD.
Let the fourth vertex of parallelogram be (x, y).
We know that, the diagonal of a parallelogram bisect each other.


Question 35.
If D (\(\frac { -1 }{ 2 }\), \(\frac { 5 }{ 2 }\)) E (7, 3) and F (\(\frac { 7 }{ 2 }\), \(\frac { 7 }{ 2 }\)) are the mid-points of sides of ∆ABC, find the area of ∆ABC. [NCERT Exemplar]
Solution:



14.5 Q 1

Ex 14.5 Q1 i
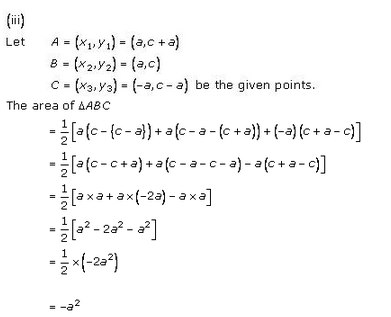
Chapter 14 Ex 14.5 Q2

Ex 14.5 Q2 i

Ex 14.5 Q2 ii
Ex 14.5 Q3

Coordinate Geometry Ex 14.5 Q4
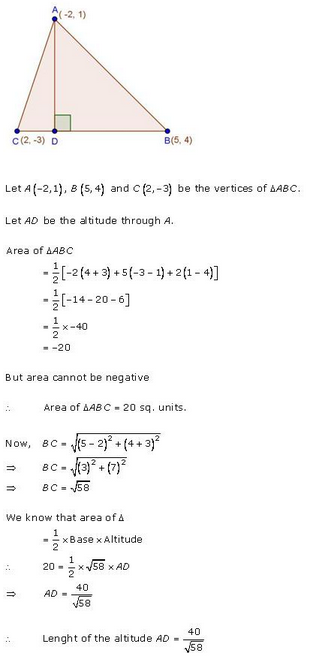
Coordinate Geometry Ex 14.5 Q5

Coordinate Geometry Ex 14.5 Q6

RD Sharma Class 10 Solutions Ex 14.5 Q7

RD Sharma Class 10 Solutions Ex 14.5 Q8

RD Sharma Class 10 Solutions Ex 14.5 Q9
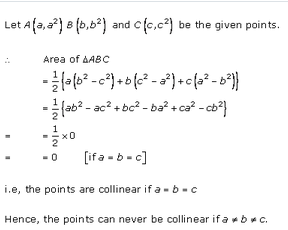
RD Sharma Class 10 Solutions Ex 14.5 Q10
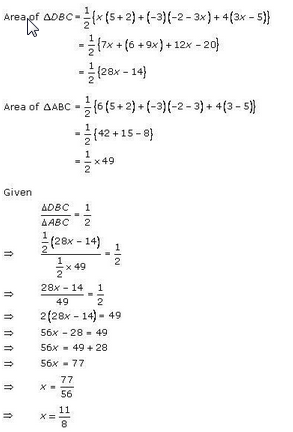
RD Sharma Class 10 Solutions Ex 14.5 Q11
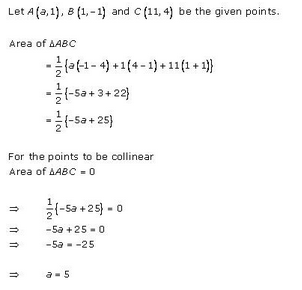
RD Sharma Class 10 Solutions Ex 14.5 Q12
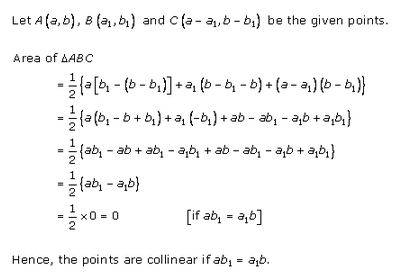
RD Sharma Class 10 Solutions
- Chapter 14 Co-Ordinate Geometry Ex 14.1
- Chapter 14 Co-Ordinate Geometry Ex 14.2
- Chapter 14 Co-Ordinate Geometry Ex 14.3
- Chapter 14 Co-Ordinate Geometry Ex 14.4
- Chapter 14 Co-Ordinate Geometry Ex 14.5