RD Sharma Class 10 Solutions Chapter 11 Constructions Exercise 11.3
RD Sharma Class 10 Solutions Constructions Exercise 11.3
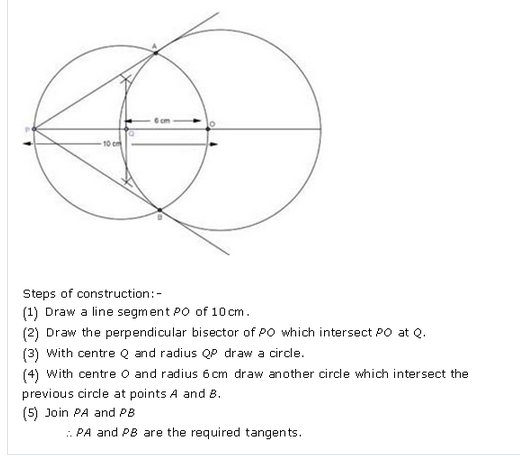
Question 1.
Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths.
Solution:
Steps of construction :
(i) Draw a circle with O centre and 6 cm radius.
(ii) Take a point P, 10 cm away from the centre O.
(iii) Join PO and bisect it at M.
(iv) With centre M and diameter PO, draw a circle intersecting the given circle at T and S.
(v) Join PT and PS.
Then PT and PS are the required tangents.

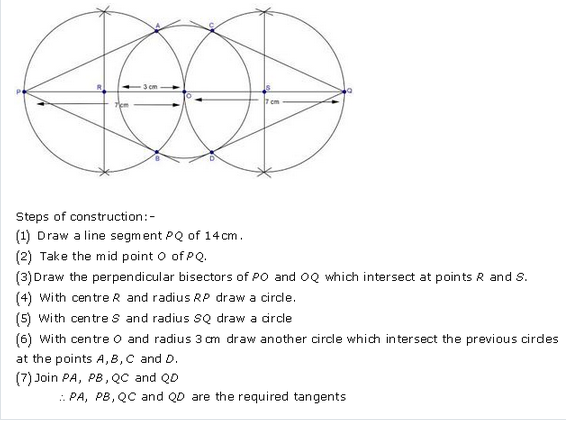
Question 2.
Draw a circle of radius 3 cm. Take two points P and Q on one of its extended diameter each at a distance of 7 cm from its centre. Draw tangents to the circle from these two points P and Q.
Solution:
Steps of construction :
(i) Draw a circle with centre O and radius 3 cm.
(ii) Draw a diameter and produce it to both sides.
(iii) Take two points P and Q on this diameter with a distance of 7 cm each from the centre O.
(iv) Bisect PO at M and QO at N
(v) With centres M and N, draw circle on PO and QO as diameter which intersect the given circle at S, T and S’, T’ respectively.
(vi) Join PS, PT, QS’ and QT’.
Then PS, PT, QS’ and QT’ are the required tangents to the given circle.

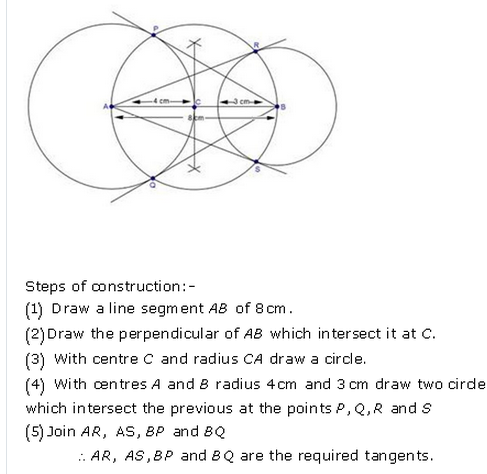
Question 3.
Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm and taking B as centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle. [CBSE 2013]
Solution:
Steps of construction :
(i) Draw a line segment AB = 8 cm.
(ii) With centre A and radius 4 cm and with centre B and radius 3 cm, circles are drawn.
(iii) Bisect AB at M.
(iv) With centre M and diameter AB, draw a circle which intersects the two circles at S’, T’ and S, T respectively.
(v) Join AS, AT, BS’and BT’.
Then AS, AT, BS’ and BT’ are the required tangent.

Question 4.
Draw two tangents to a circle of raidus 3.5 cm from a point P at a distance of 6.2 cm from its centre.
Solution:
Steps of construction :
(i) Draw a circle with centre O and radius 3.5 cm
(ii) Take a point P which is 6.2 cm from O.
(iii) Bisect PO at M and draw a circle with centre M and diameter OP which intersects the given circle at T and S respectively.
(iv) Join PT and PS.
PT and PS are the required tangents to circle.

Question 5.
Draw a pair of tangents to a circle of radius 4.5 cm, which are inclined to each other at an angle of 45°. [CBSE 2013]
Solution:
Steps of construction :
Angle at the centre 180° – 45° = 135°
(i) Draw a circle with centre O and radius 4.5 cm.

(ii) At O, draw an angle ∠TOS = 135°
(iii) At T and S draw perpendicular which meet each other at P.
PT and PS are the tangents which inclined each other 45°.
Question 6.
Draw a right triangle ABC in which AB = 6 cm, BC = 8 cm and ∠B = 90°. Draw BD perpendicular from B on AC and draw a circle passing through the points B, C and D. Construct tangents from A to this circle.
Solution:
Steps of Construction :
Draw a line segment BC = 8 cm
From B draw an angle of 90°
Draw an arc \(\breve { BA }\) = 6cm cutting the angle at A.
Join AC.
ΔABC is the required A.
Draw ⊥ bisector of BC cutting BC at M.
Take M as centre and BM as radius, draw a circle.
Take A as centre and AB as radius draw an arc cutting the circle at E. Join AE.
AB and AE are the required tangents.
Justification :
∠ABC = 90° (Given)
Since, OB is a radius of the circle.
∴ AB is a tangent to the circle.
Also AE is a tangent to the circle.

Question 7.
Draw two concentric circles of radii 3 cm and 5 cm. Construct a tangent to the smaller circle from a point on the larger circle. Also, measure its length. [CBSE 2016]
Solution:
Given, two concentric circles of radii 3 cm and 5 cm with centre O. We have to draw pair of tangents from point P on outer circle to the other.

Steps of construction :
(i) Draw two concentric circles with centre O and radii 3 cm and 5 cm.
(ii) Taking any point P on outer circle. Join OP.
(iii) Bisect OP, let M’ be the mid-point of OP.
Taking M’ as centre and OM’ as radius draw a circle dotted which cuts the inner circle as M and P’.
(iv) Join PM and PP’. Thus, PM and PP’ are the required tangents.
(v) On measuring PM and PP’, we find that PM = PP’ = 4 cm.
Actual calculation:
In right angle ΔOMP, ∠PMO = 90°
∴ PM2 = OP2 – OM2
[by Pythagoras theorem i.e. (hypotenuse)2 = (base)2 + (perpendicular)2]
⇒ PM2 = (5)2 – (3)2 = 25 – 9 = 16
⇒ PM = 4 cm
Hence, the length of both tangents is 4 cm.
RD Sharma Class 10th Solutions Chapter 11 Constructions Exercise 11.3 Q1
RD Sharma Class 10 Solutions Chapter 11 Constructions Exercise 11.3 Q2
Q3
RD Sharma Class 10 Solutions