RD Sharma Class 10 Solutions Chapter 11 Constructions Exercise 11.1
RD Sharma Class 10 Solutions Constructions Exercise 11.1
Question 1.
Determine a point which divides a line segment of length 12 cm internally in the ratio 2 : 3. Also justify your construction.
Solution:
Steps of construction :
(i) Draw a line segment AB = 12 cm.
(ii) Draw a ray AX at A making an acute angle with AB.
(iii) From B, draw another ray BY parallel to AX.
(iv) Cut off 2 equal parts from AX and 3 equal parts from BY.
(v) Join 2 and 3 which intersects AB at P.
P is the required point which divides AB in the ratio of 2 : 3 internally.

Question 2.
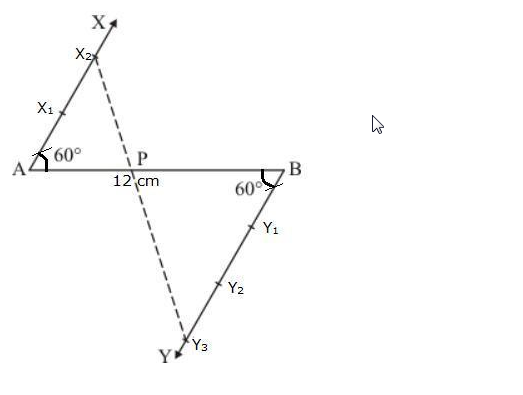
Divide a line segment of length 9 cm internally in the ratio 4 : 3. Also, give justification of the construction.
Solution:
Steps of construction :
(i) Draw a line segment AB = 9 cm.
(ii) Draw a ray AX making an acute angle with AB.
(iii) From B, draw another ray BY parallel to AX.
(iv) Cut off 4 equal parts from AX and 3 parts from BY.
(v) Join 4 and 3 which intersects AB at P.
P is the required point which divides AB in the ratio of 4 : 3 internally.

Question 3.
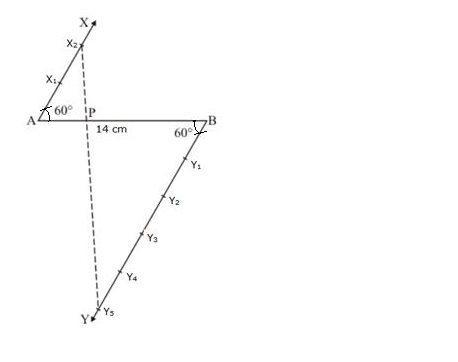
Divide a line segment of length 14 cm internally in the ratio 2 : 5. Also justify your construction.
Solution:
Steps of construction :
(i) Draw a line segment AB = 14 cm.
(ii) Draw a ray AX making an acute angle with AB.
(iii) From B, draw another ray BY parallel to AX.
(iv) From AX, cut off 2 equal parts and from B, cut off 5 equal parts.
(v) Join 2 and 5 which intersects AB at P.
P is the required point which divides AB in the ratio of 2 : 5 internally.

Question 4.
Draw a line segment of length 8 cm and divide it internally in the ratio 4 : 5.
Solution:
Steps of construction :
(i) Draw a line segment AB = 8 cm.
(ii) Draw a ray AX making an acute angle with ∠BAX = 60° withAB.

(iii) Draw a ray BY parallel to AX by making an acute angle ∠ABY = ∠BAX.
(iv) Mark four points A1, A2, A3, A4 on AX and five points B1, B2, B3, B4, Bs on BY in such a way that AA1 = A1A2 = A2A3 = A3A4 .
(v) Join A4B5.
(vi) Let this line intersect AB at a point P.
Thus, P is the point dividing the line segment AB internally in the ratio of 4 : 5.
RD Sharma Class 10 Solutions Chapter 11 Constructions Exercise 11.1
Q1.

RD Sharma Class 10 Solutions Chapter 11 Constructions Exercise 11.1 Q2


RD Sharma Class 10 Solutions Chapter 11 Constructions Exercise 11.1 Q3