NCERT Solutions for Class 8 Maths Chapter 8 Comparing Quantities Ex 8.3
- Class 8 Maths Comparing Quantities Exercise 8.1
- Class 8 Maths Comparing Quantities Exercise 8.2
- Class 8 Maths Comparing Quantities Exercise 8.3
- Comparing Quantities Class 8 Extra Questions
NCERT Solutions for Class 8 Maths Chapter 8 Comparing Quantities Exercise 8.3
Ex 8.3 Class 8 Maths Question 1.
Calculate the amount and compound interest on
(a) ₹ 10,800 for 3 years at 12\(\frac { 1 }{ 2 }\) % per annum compounded annually.
(b) ₹ 18,000 for 2\(\frac { 1 }{ 2 }\) years at 10% per annum compounded annually.
(c) ₹ 62,500 for 1\(\frac { 1 }{ 2 }\) years at 8% per annum compounded half yearly.
(d) ₹ 8,000 for 1 year at 9% per annum compounded half yearly. (You could use the year by year calculation using SI formula to verify).
(e) ₹ 10,000 for 1 year at 8% per annum compounded half yearly.
Solution:
(a) Given:
P = ₹ 10,800, n = 3 years,
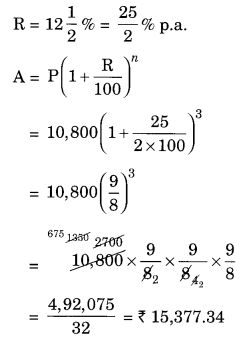
CI = A – P = ₹ 15,377.35 – ₹ 10,800 = ₹ 4,577.35
Hence amount = ₹ 15,377.34 and CI = ₹ 4,577.34
(b) Given: P = ₹ 18,000, n = 2\(\frac { 1 }{ 2 }\) years = \(\frac { 5 }{ 2 }\) years
R = 10% p.a.
The amount for 2\(\frac { 1 }{ 2 }\) years, i.e., 2 years and 6 months can be calculated by first calculating the amount to 2 years using CI formula and then calculating the simple interest by using SI formula.
The amount for 2 years has to be calculated

Total CI = ₹ 3780 + ₹ 1089 = ₹ 4,869
Amount = P + I = ₹ 21,780 + ₹ 1,089 = ₹ 22,869
Hence, the amount = ₹ 22,869
and CI = ₹ 4,869
(c) Given: P = ₹ 62,500, n = 1\(\frac { 1 }{ 2 }\) years = \(\frac { 3 }{ 2 }\) years per annum compounded half yearly
= \(\frac { 3 }{ 2 }\) × 2 years = 3 half years
R = 8% = \(\frac { 8 }{ 2 }\) % = 4% half yearly
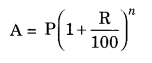
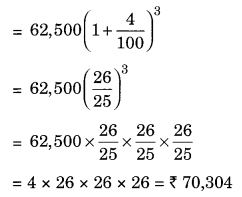
CI = A – P = ₹ 70,304 – ₹ 62,500 = ₹ 7,804
Hence, amount = ₹ 70304 and CI = ₹ 7804
(d) Given: P = ₹ 8,000, n = 1 years R = 9% per annum compounded half yearly
Since, the interest is compounded half yearly n = 1 × 2 = 2 half years
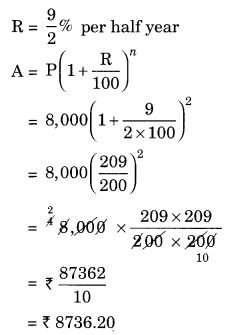
CI = A – P = ₹ 8,736.20 – ₹ 8,000 = ₹ 736.20
Hence, the amount = ₹ 8736.20 and CI = ₹ 736.20
(e) Given: P = ₹ 10,000, n = 1 year and R = 8% pa compounded half yearly
Since the interest is compounded half yearly n = 1 × 2 = 2 half years
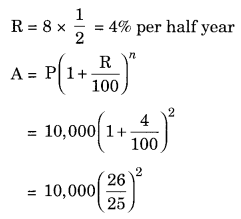
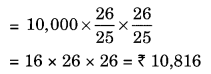
CI = A – P = ₹ 10,816 – ₹ 10,000 = ₹ 816
Hence the amount = ₹ 10,816 and Cl = ₹ 816
Ex 8.3 Class 8 Maths Question 2.
Kamala borrowed ₹ 26,400 from a Bank to buy a scooter at a rate of 15% per annum compounded yearly. What amount will she pay at the end of 2 years and 4 months to clear the loan? (Hint: Find amount for 2 years with interest is compounded yearly and then find SI on the 2nd
year amount for \(\frac { 4 }{ 12 }\) years).
Solution:
Given:
P = ₹ 26,400
R = 15% p.a. compounded yearly
n = 2 years and 4 months

Amount after 2 years and 4 months = ₹ 34,914 + ₹ 1745.70 = ₹ 36,659.70
Hence, the amount to be paid by Kamla = ₹ 36,659.70
Ex 8.3 Class 8 Maths Question 3.
Fabina borrows ₹ 12,500 at 12% per annum for 3 years at simple interest and Radha borrows the same amount for the same time period at 10% per annum, compounded annually. Who pays more interest and by how much?
Solution:
For Fabina: P = ₹ 12,500, R = 12% p.a. and n = 3 years
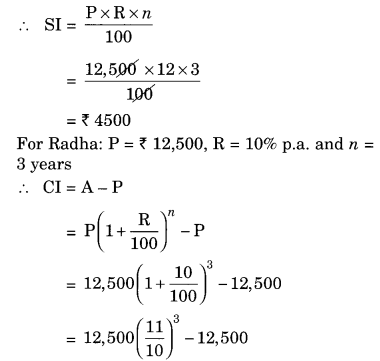

Difference between the two interests = ₹ 4500 – ₹ 4137.50 = ₹ 362.50
Hence, Fabina pays more interest by ₹ 362.50.
Ex 8.3 Class 8 Maths Question 4.
I borrowed ₹ 12,000 from Jamshed at 6% per annum simple interest for 2 years. Had I borrowed this sum at 6% per annum compound interest, what extra amount would I have to pay?
Solution:
Given: P = ₹ 12,000, R = 6% p.a., n = 2 years
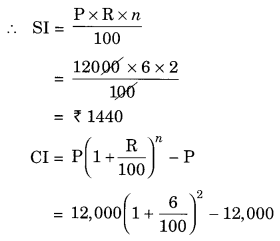

Difference between two interests = ₹ 1483.20 – ₹ 1440 = ₹ 43.20
Hence, the extra amount to be paid = ₹ 43.20
Ex 8.3 Class 8 Maths Question 5.
Vasudevan invested ₹ 60,000 at an interest rate of 12% per annum compounded half yearly. What amount would he get
(i) after 6 months?
(ii) after 1 year?
Solution:
(i) Given: P = ₹ 60,000, R = 12% p.a. compounded half yearly

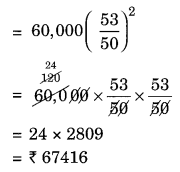
Hence, the required amount = ₹ 67416
Ex 8.3 Class 8 Maths Question 6.
Arif took a loan of ₹ 80,000 from a bank. If the rate of interest is 10% per annum, find the difference in amounts he would be paying after
1\(\frac { 1 }{ 2 }\) years if the interest is
(i) compounded annually.
(ii) compounded half yearly.
Solution:
(i) Given: P = ₹ 80,000
R = 10% p.a.
n = 1\(\frac { 1 }{ 2 }\) years
Since the interest is compounded annually
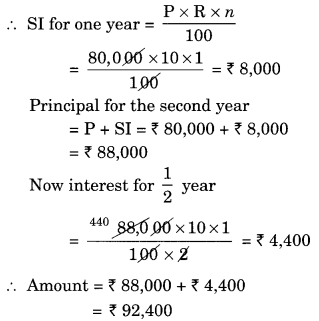
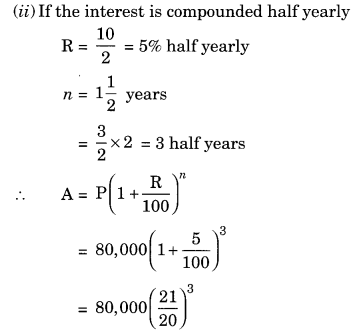
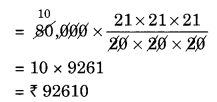
Difference between the amounts = ₹ 92,610 – ₹ 92,400 = ₹ 210
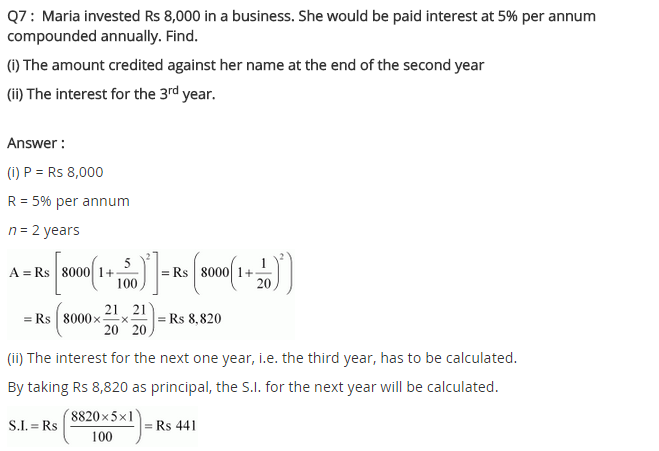
Ex 8.3 Class 8 Maths Question 7.
Maria invested ₹ 8,000 in a business. She would be paid interest at 5% per annum compounded annually. Find
(i) The amount credited against her name at the end of the second year.
(ii) The interest for the third year.
Solution:
(i) Given: P = ₹ 8,000, R = 5% p.a.
and n = 2 years

Hence, interest for the third year = ₹ 441
Ex 8.3 Class 8 Maths Question 8.
Find the amount and the compound interest on ₹ 10,000 for 1\(\frac { 1 }{ 2 }\) years at 10% per annum, compounded half yearly. Would this interest be more than the interest he would get if it was compounded annually?
Solution:
Given: P = ₹ 10,000, n = 1\(\frac { 1 }{ 2 }\) years
R = 10% per annum
Since the interest is compounded half yearly
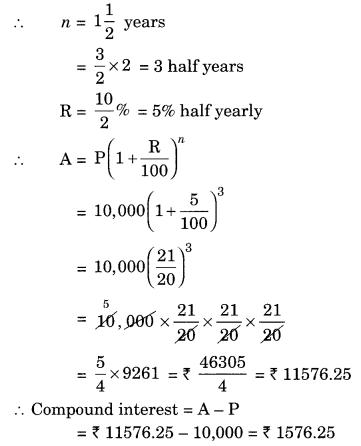

Total interest = ₹ 1,000 + ₹ 550 = ₹ 1,550
Difference between the two interests = ₹ 1,576.25 – ₹ 1,550 = ₹ 26.25
Hence, the interest will be ₹ 26.25 more when compounded half yearly than the interest when compounded annually.
Ex 8.3 Class 8 Maths Question 9.
Find the amount which Ram will get on ₹ 4,096, if he gave it for 18 months at 12\(\frac { 1 }{ 2 }\) per annum, interest being compounded half yearly.
Solution:
Given: P = ₹ 4,096, R = 12\(\frac { 1 }{ 2 }\) % pa, n = 18 months
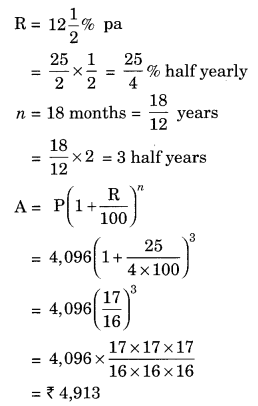
Hence, the required amount = ₹ 4913
Ex 8.3 Class 8 Maths Question 10.
The population of a place increased to 54,000 in 2003 at a rate of 5% per annum.
(i) Find the population in 2001.
(ii) What would be its population in 2005?
Solution:
(i) Given: Population in 2003 = 54,000
Rate = 5% pa
Time = 2003 – 2001 = 2 years
Population in 2003 = Population in 2001

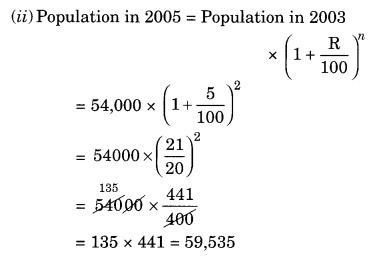
Ex 8.3 Class 8 Maths Question 11.
In a Laboratory, the count of bacteria in a certain experiment was increasing at the rate of 2.5% per hour. Find the bacteria at the end of 2 hours if the count was initially 5,06,000.
Solution:
Given: Initial count of bacteria = 5,06,000
Rate = 2.5% per hour
n = 2 hours
Number of bacteria at the end of 2 hours = Number of count of bacteria initially
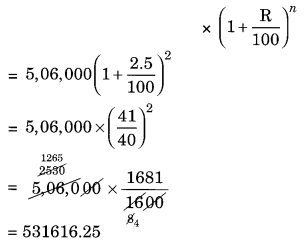
Thus, the number of bacteria after two hours = 5,31,616 (approx).
Ex 8.3 Class 8 Maths Question 12.
A scooter was bought at ₹ 42,000. Its value depreciated at the rate of 8% per annum. Find its value after one year.
Solution:
Given: Cost price of the scooter = ₹ 42,000
Rate of depreciation = 8% p.a.
Time = 1 year
Final value of the scooter
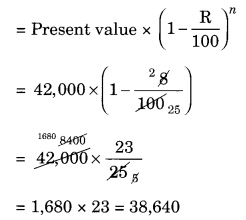
Hence, the value of scooter after 1 year = ₹ 38,640.



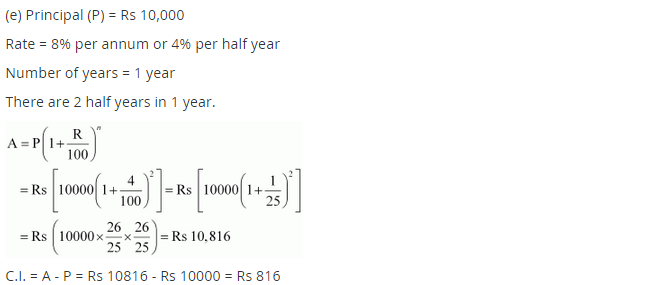





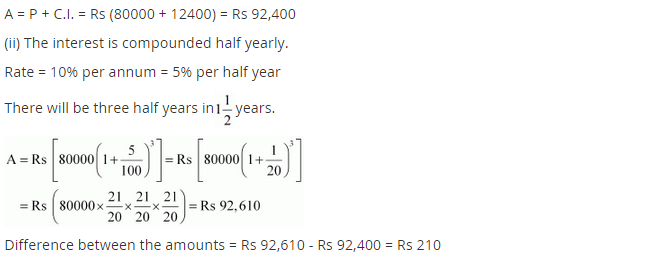




More CBSE Class 8 Study Material
- NCERT Solutions for Class 8 Maths
- NCERT Solutions for Class 8 Science
- NCERT Solutions for Class 8 Social Science
- NCERT Solutions for Class 8 English
- NCERT Solutions for Class 8 English Honeydew
- NCERT Solutions for Class 8 English It So Happened
- NCERT Solutions for Class 8 Hindi
- NCERT Solutions for Class 8 Sanskrit
- NCERT Solutions