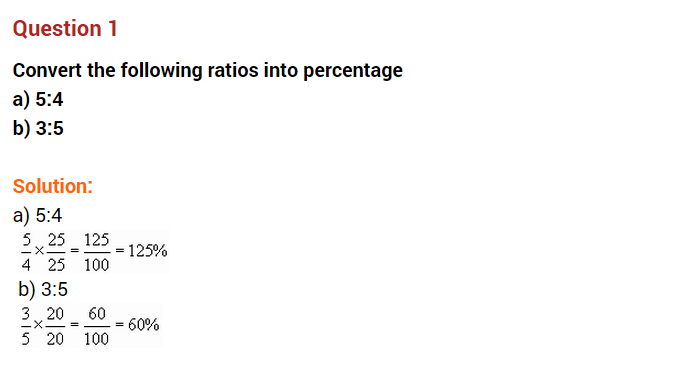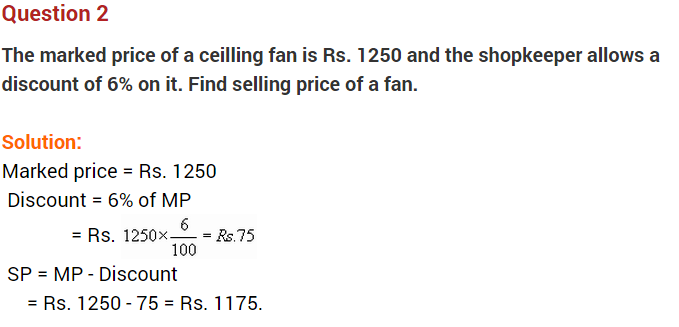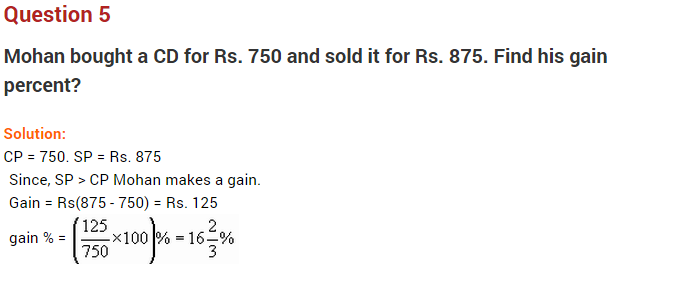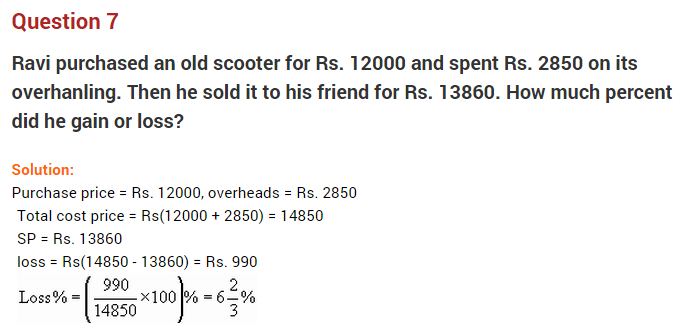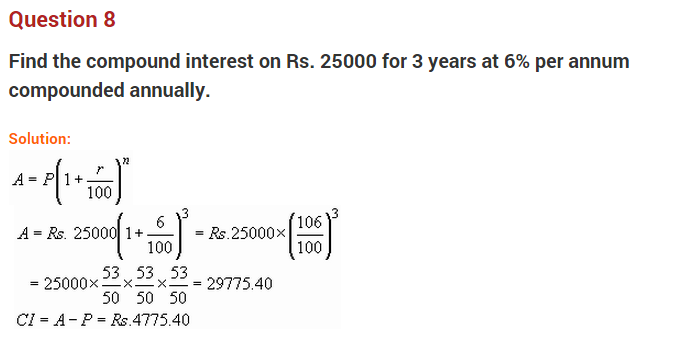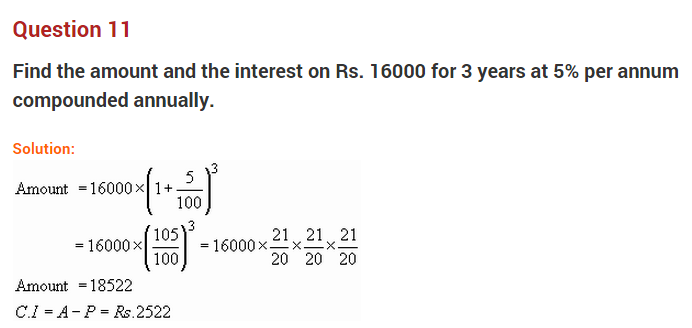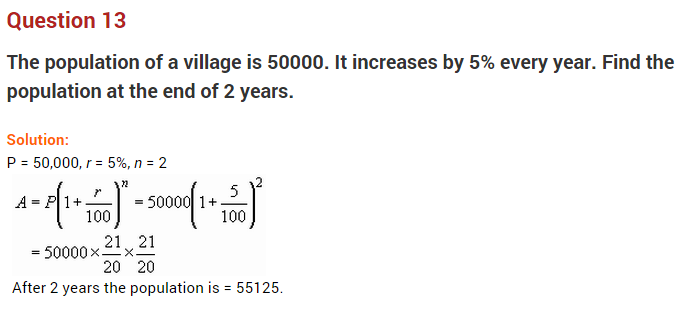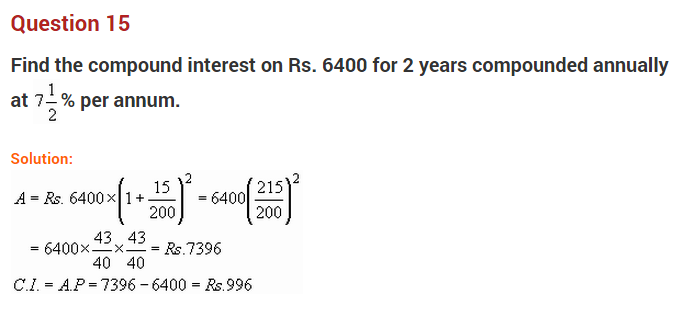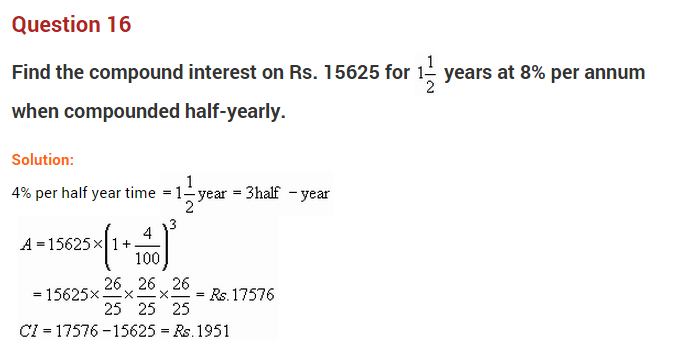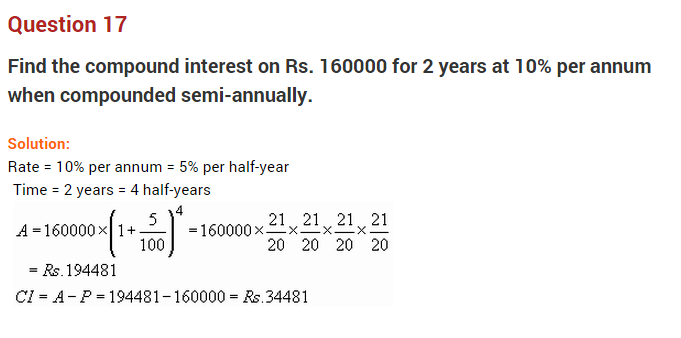Comparing Quantities Class 8 Extra Questions Maths Chapter 8
Extra Questions for Class 8 Maths Chapter 8 Comparing Quantities
Comparing Quantities Class 8 Extra Questions Very Short Answer Type
Question 1.
Express the following in decimal form:
(a) 12%
(b) 25%
Solution:
(a) 12% = \(\frac { 12 }{ 100 }\) = 0.12
(b) 25% = \(\frac { 25 }{ 100 }\) = 0.25
Question 2.
Evaluate the following:
(a) 20% of 400
(b) 12\(\frac { 1 }{ 2 }\)% of 625
Solution:

Question 3.
If 20% of x is 25, then find x.
Solution:
20% of x = 25

Hence x = 125
Question 4.
Express the following as a fraction
(a) 35%
(b) 64%
Solution:

Question 5.
Express the following into per cent
(а) 1\(\frac { 3 }{ 5 }\)
(b) 2 : 5
Solution:

Question 6.
There are 24% of boys in a school. If the number of girls is 456, find the total number of students in the school.
Solution:
Let the total number of students be 100.
Number of boys = 24% of 100 = \(\frac { 24 }{ 100 }\) × 100 = 24
Number of girls = 100 – 24 = 76
⇒ If number of girls is 76, then total number of students = 100
⇒ If Number of girls is 1, then total number of students = \(\frac { 100 }{ 76 }\)
If Number of girls is 456, then total number of students = \(\frac { 100\times 456 }{ 76 }\) = 600
Hence, the total number of students in the school = 600
Question 7.
The cost of 15 articles is equal to the selling price of 12 articles. Find the profit per cent.
Solution:
Let CP of 15 articles be ₹ 100
CP of 1 article = ₹ \(\frac { 100 }{ 15 }\)
SP of 12 articles = ₹ 100
SP fo 1 article = ₹ \(\frac { 100 }{ 12 }\)
SP > CP


Hence, profit = 25%
Question 8.
An article is marked at ₹ 940. If it is sold for ₹ 799, then find the discount per cent.
Solution:
MP = ₹ 940
SP = ₹ 799
Discount = MP – SP = 940 – 799 = ₹ 141

Hence, discount = 15%
Question 9.
A watch was bought for ₹ 2,700 including 8% VAT. Find its price before the VAT was added.
Solution:
Cost of watch including VAT = ₹ 2,700
Let the initial cost of the watch be ₹ 100
VAT = 8% of ₹ 100 = ₹ 8
Cost of watch including VAT = ₹ 100 + ₹ 8 = ₹ 108
If cost including VAT is ₹ 108, then its initial cost = ₹ 100
If cost including VAT is ₹ 1, then its initial cost = ₹ \(\frac { 100 }{ 108 }\)
If cost including VAT is ₹ 2,700, then its initial cost = ₹ \(\frac { 100 }{ 108 }\) × 2700 = ₹ 2500
Hence, the required cost = ₹ 2,500
Question 10.
Find the amount if ₹ 2,000 is invested for 2 years at 4% p.a. compounded annually.
Solution:


Comparing Quantities Class 8 Extra Questions Short Answer Tpye
Question 11.
A number is increased by 20% and then it is decreased by 20%. Find the net increase or decrease per cent. (NCERT Exemplar)
Solution:
Let the number be 100
20% increase = \(\frac { 20 }{ 100 }\) × 100 = 20
Increased value = 100 + 20 = 120
Now it is decreased by 20%
Decreased value = 120 – \(\frac { 120 }{ 100 }\) × 20 = 120 – 24 = 96
Net decrease = 100 – 96 = 4
Decrease per cent = \(\frac { 4 }{ 100 }\) × 100 = 4%
Hence, the net decrease per cent = 4%
Question 12.
Two candidates Raman and Rajan contested an election. Raman gets 46% of the valid votes and is#defeated by 1600 votes. Find the total number of valid votes cast in the election.
Solution:
Let the total number of valid votes be 100
Number of votes got by Raman = 46% of 100 = \(\frac { 46 }{ 100 }\) × 100 = 46
Number of votes got by Rajan = 100 – 46 = 54
Difference between the votes = 54 – 46 = 8
8% of Valid votes = 1,600
⇒ \(\frac { 8 }{ 100 }\) × Valid votes = 1,600
⇒ Valid votes = \(\frac { 1600\times 100 }{ 8 }\) = 20,000
Hence, the total number of valid votes = 20,000
Question 13.
A man whose income is ₹ 57,600 a year spends ₹ 43,200 a year. What percentage of his income does he save?
Solution:
Annual income of a man = ₹ 57,600
Amount spent by him in the year = ₹ 43,200
Net amount saved by him = ₹ 57,600 – ₹ 43,200 = ₹ 14,400
Percentage of his annual saving Saving = \(\frac { Saving }{ Income }\) × 100
= \(\frac { 14400 }{ 57600 }\) × 100
= 25%
Hence, the saving percentage = 25%
Question 14.
A CD player was purchased for ₹ 3,200 and ₹ 560 were spent on its repairs. It was then sold at a gain of 12\(\frac { 1 }{ 2 }\) %. How much did the seller receive?
Solution:
Cost price of the CD player = ₹ 3,200
Amount spent on its repairing = ₹ 560
Net cost price = ₹ 3,200 + ₹ 560 = ₹ 3,760

Hence, the required amount = ₹ 4,230
Question 15.
A car is marked at ₹ 3,00,000. The dealer allows successive discounts of 6%, 4% and 2\(\frac { 1 }{ 2 }\) % on it. What is the net selling price of it?
Solution:
Marked price of the car = ₹ 3,00,000
Net selling price after the successive discounts

Hence, the net selling price = ₹ 2,63,952
Question 16.
Ramesh bought a shirt for ₹ 336, including 12% ST and a tie for ₹ 110 including 10% ST. Find the list price (without sales tax) of the shirt and the tie together.
Solution:
List price of the shirt = \(\frac { 110 }{ 112 }\) × 336 = ₹ 300
List price of the tie = \(\frac { 100 }{ 110 }\) × 110 = ₹ 100
List price of both together = ₹ 300 + ₹ 100 = ₹ 400
Question 17.
Find the amount of ₹ 6,250 at 8% pa compounded annually for 2 years. Also, find the compound interest.
Solution:

Question 18.
Find the compound interest on ₹ 31,250 at 12% pa for 12\(\frac { 1 }{ 2 }\) years.
Solution:

Question 19.
Vishakha offers a discount of 20% on all the items at her shop and still makes a profit of 12%. What is the cost price of an article marked at ₹ 280? (NCERT Exemplar)
Solution:
Marked Price = ₹ 280
Discount = 20% of ₹ 280
= \(\frac { 1 }{ 2 }\) × 280 = ₹ 56
So selling price = ₹ (280 – 56) = ₹ 224
Let the cost price be ₹ 100
Profit = 12% of ₹ 100 = ₹ 12
So selling price = ₹ (100 + 12) = ₹ 112
If the selling price is ₹ 112, cost price = ₹ 100
If the selling price is ₹ 224, cost price = ₹ (\(\frac { 100 }{ 112 }\) × 224) = ₹ 200
Question 20.
Find the compound interest on ₹ 48,000 for one year at 8% per annum when compounded half yearly. (NCERT Exemplar)
Solution:
Principal (P) = ₹ 48,000
Rate (R) = 8% p.a.
Time (n) = 1 year
Interest is compounded half yearly

Therefore Compound Interest = A – P = ₹ (519,16.80 – 48,000) = ₹ 3,916.80.