Get Free NCERT Solutions for Class 11 Maths Chapter 10 Straight Lines Ex 10.3. Class 11 Maths NCERT Solutions are extremely helpful while doing homework. Exercise 10.3 Class 11 Maths NCERT Solutions were prepared by Experienced LearnCBSE.in Teachers. Detailed answers of all the questions in Chapter 10 Maths Straight Lines Class 11 Exercise 10.3 Provided in NCERT Textbook.
- Straight Lines Class 11 Ex 10.1
- Straight Lines Class 11 Ex 10.2
- Straight Lines Class 11 Ex 10.3
- Straight Lines Class 11 Miscellaneous Exercise
- सरल रेखाएँ प्रश्नावली 10.1 का हल हिंदी में
- सरल रेखाएँ प्रश्नावली 10.2 का हल हिंदी में
- सरल रेखाएँ प्रश्नावली 10.3 का हल हिंदी में
- सरल रेखाएँ विविध प्रश्नावली का हल हिंदी में
- Straight Lines Class 11 Notes
- Straight Lines NCERT Exemplar Class 11 Solutions
- RD Sharma Class 11 Solutions Straight Lines
- JEE Main Mathematics Straight Lines Previous Year Questions
You can also save the NCERT Solutions Class 11 Maths Straight Lines images and take the print out to keep it handy for your exam preparation.
Topics and Sub Topics in Class 11 Maths Chapter 10 Straight Lines:
| Section Name | Topic Name |
| 10 | Straight Lines |
| 10.1 | Introduction |
| 10.2 | Slope of Line |
| 10.3 | Various Forms of the Equation of Line |
| 10.4 | General Equation of Line |
| 10.5 | Distance of a Point From a Line |
NCERT Solutions for Class 11 Maths Chapter 10 Straight Lines Ex 10.3

NCERT Solutions for Class 11 Maths Chapter 10 Straight Lines Ex 10.3 are part of NCERT Solutions for Class 11 Maths. Here we have given Class 11 Maths NCERT Solutions Straight Lines Ch 10 Exercise 10.3.
Ex 10.3 Class 11 Maths Question-1

Ans.


Ex 10.3 Class 11 Maths Question-2
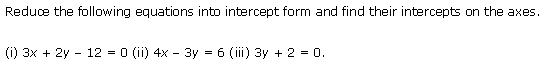
Ans.


Ex 10.3 Class 11 Maths Question-3

Ans.



Ex 10.3 Class 11 Maths Question-4
![]()
Ans.

Ex 10.3 Class 11 Maths Question-5
![]()
Ans.

Ex 10.3 Class 11 Maths Question-6
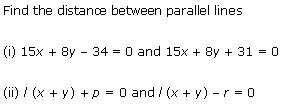
Ans.

Ex 10.3 Class 11 Maths Question-7
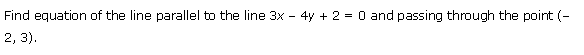
Ans.

Ex 10.3 Class 11 Maths Question-8
![]()
Ans.

Ex 10.3 Class 11 Maths Question-9
![]()
Ans.

Ex 10.3 Class 11 Maths Question-10
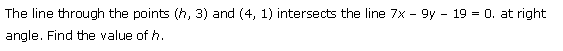
Ans.

Ex 10.3 Class 11 Maths Question-11
![]()
Ans.

Ex 10.3 Class 11 Maths Question-12

Ans.



Ex 10.3 Class 11 Maths Question-13
![]()
Ans.

Ex 10.3 Class 11 Maths Question-14
![]()
Ans.


Ex 10.3 Class 11 Maths Question-15

Ans.

Ex 10.3 Class 11 Maths Question-16

Ans.


Ex 10.3 Class 11 Maths Question-17
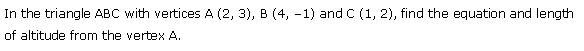
Ans.


Ex 10.3 Class 11 Maths Question-18

Ans.


NCERT Solutions for Class 11 Maths Chapter 10 Straight Lines (सरल रेखाएँ) Hindi Medium Ex 10.3



















Maths NCERT Solutions Class 11 Maths Chapter 10 Exercise.10.3
Q1. Reduce the following equations into slope-intercept form and find their slopes and the y intercepts.
(i) x + 6y = 0
(ii) 6x + 3y – 6 = 0
(iii) y = 1
Q2. Reduce the following equations into intercept form and find their intercepts on the axes.
(i) 3x + 2y – 14 = 0
(ii) 4x – 3y = 6
(iii) 3y + 2 = 0
Q3. Reduce the following equations into normal form. Find their perpendicular distances from the origin and angle between perpendicular and the positive x-axis.
(i) x–√3y+8=0
(ii) y – 2 = 0
(iii) x – y = 4
Q4. Find the distance of the point (–1, 1) from the line 12(x + 6) = 5(y – 2).
Q6. Find the distance between parallel lines
(i) 15x + 8y – 34 = 0 and 15x + 8y + 31 = 0
(ii) l (x + y) + p = 0 and l (x + y) – r = 0
Q7. Find equation of the line parallel to the line 3x – 4y + 2 = 0 and passing through the point (–2, 3).
Q8. Give equation of the line perpendicular to the line x – 7y + 5 = 0 and having x intercept 3.
Q9. Calculate angles between the lines √3x+y=1 and x+√3y=1
Q10. A line passes through points (k, 3)(4, 1) intersects the line 7x – 9y – 19 = 0, at right angle. Find the value of k.
Q11. Prove that the line through the point (xa, ya) and parallel to the line Ax + By + C = 0 is A(x – xa) + B (y – ya) = 0.
Q12. The angle between the two lines is 60° at intersection and passes through the point (2, 3). Obtain the slope of a second line when the slope of first line is 2.
Q13 A line segment joining the points (4, 5) and (– 2, 3). Obtain the equation of the perpendicular bisector of the line segment.
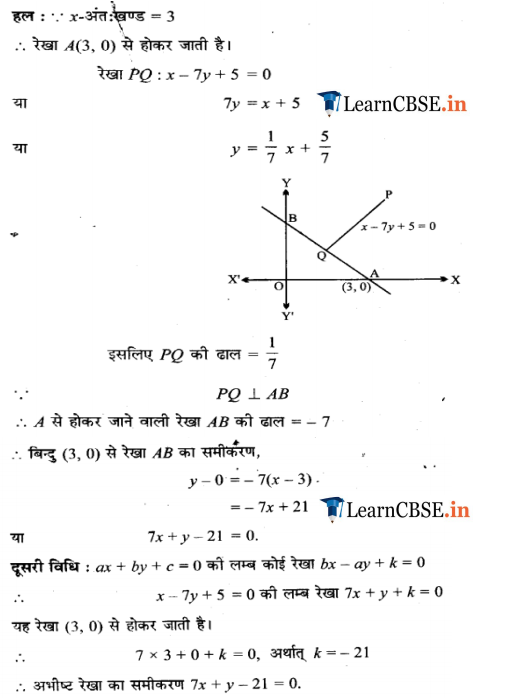
Q14: Obtain the coordinates of the foot of perpendicular from the point (– 2, 4) to the line 3x – 4y – 16 = 0.
Q15: The normal meets point (– 2, 3), is drawn from the origin to the equation of line y = m x + c.Obtain the values of m and c.
Q16: Suppose r and s are the lengths from the lines x cos θ – y sin θ = n cos 2θ and x sec θ + y cosec θ = n to the origin perpendiculars, respectively, prove that r 2 + 4 s2 = n 2
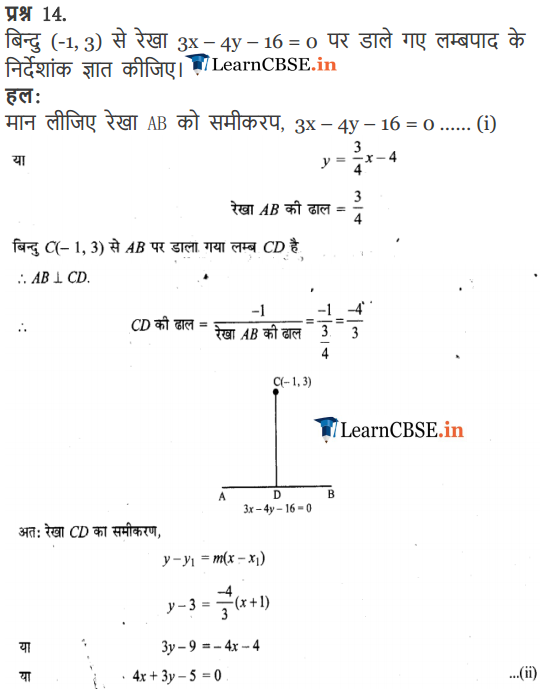
Q17: The vertices of the triangle PQR are P (3, 4), Q (5, – 2) and R (2, 3), obtain how long the altitude is from the vertex P and also obtain the equation.
Q 18: Suppose ‘r’ is the length of the origin to the line from perpendicular from the normal. The line has axes i and j axes as intercepts of the line, then prove that:
We hope the NCERT Solutions for Class 11 Maths Chapter 10 Straight Lines Ex 10.3, help you. If you have any query regarding NCERT Solutions for Class 11 Maths Chapter 10 Straight Lines Exercise 10.3, drop a comment below and we will get back to you at the earliest.