CBSE Class 10 Science Notes Chapter 12 Electricity Pdf free download is part of Class 10 Science Notes for Quick Revision. Here we have given NCERT Class 10 Science Notes Chapter 12 Electricity.
According to new CBSE Exam Pattern, MCQ Questions for Class 10 Science pdf Carries 20 Marks.
CBSE Class 10 Science Notes Chapter 12 Electricity
Electricity: Electric current, electric circuit, voltage or electric potential, resistance and (Ohm’s law).
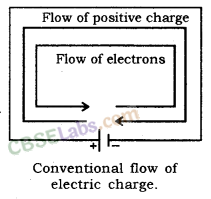
Electric Current: The flow of electric charge is known as Electric Current, Electric current is carried by moving electrons through a conductor.
By convention, electric current flows in the opposite direction to the movement of electrons.
Electric Circuit: Electric circuit is a continuous and closed path of electric current.
Expression of Electric Current: Electric current is denoted by the letter ‘I’. Electric current is expressed by the rate of flow of electric charges. Rate of flow means, the amount of charge flowing through a particular area in unit time.
If a net electric charge (Q) flows through a cross-section of a conductor in time t, then,
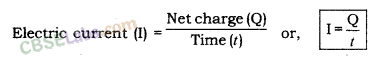
Where I is electric current, Q is a net charge and t is a time in second.
S.I. Unit of Electric Charge and Current: S.I. unit of electric charge is coulomb (C).
One coulomb is nearly equal to 6 × 1018 electrons. S.I. unit of electric current is ampere (A). Ampere is the flow of electric charge through a surface at the rate of one coulomb per second. This means, if 1 coulomb of electric charge flows through a cross section for 1 second, it would be equal to 1 ampere.
Therefore, 1 A = 1 C/1 s
Small Quantity of Electric Current: Small quantity of electric current is expressed in milliampere and microampere. Milliampere is written as mA and microampere as pA.
1 mA (milliampere) = 10-3 A
1 pA (microampere) = 10-6 A
Ammeter: An apparatus to measure electric current in a circuit.,
Charge: Like mass, the charge is the fundamental property of matter. There are two types of charge
(i) Positive charge.
(ii) Negative charge.
Positive and Negative Charge: The charge acquired by a glass rod when rubbed with silk is called a positive charge and the charge acquired by an ebonite rod when rubbed with wool is called negative charge.
Properties of Electric Charge:
(i) Unlike charges attract each other and like charges repel each other.
(ii) The.force between two charges varies directly as the product of two charges and inversely as the square of the distance (r) between both charges (q1 and q2).

S.I. unit of charge is coulomb (C).
1 coulomb = 1 ampere × 1 second.
1C = 1A × 1s
Thus, the quantity of charge which flows through a circuit when one ampere of current flows through it in one second is known as a 1-coulomb charge.
Electric Potential and Potential Difference
Electric Potential: The amount of electric potential energy at a point is called electric potential.
Potential Difference: The difference in the amount of electric potential energy between two points in an electric circuit is called electric potential difference.
Electric potential difference is known as voltage, which is equal to the amount of work done to move the unit charge between two points against static electric field.
Therefore, Voltage = \(\frac { Workdone }{ Charge }\)
Voltage or electric potential difference is denoted by V’. Therefore, V = \(\frac { W }{ Q }\)
Where, W = Work done and Q = Charge
S.I. Unit of Electric Potential Difference (Voltage)
S.I. unit of electric potential difference is volt and denoted by ‘V’ This is named in honour of Italian Physicist Alessandro Volta.
Since joule is the unit of work and Coulomb is the unit of charge, 1 volt of electric potential difference is equal to the 1 joule of work to be done to move a charge of 1 coulomb from one point to another in an electric circuit. Therefore
1V = 1Joule/1Coulomb = 1J/1C
1V = 1JC-1
Voltmeter: An apparatus to measure the potential difference or electric potential difference between two points in an electric circuit.
Galvanometer: It is a device to detect current in an electric circuit.
Ohm’s Law: Ohm’s Law states that the potential difference between two points is directly proportional to the electric current, at a constant temperature.
This means potential difference V varies as electric current.
V ∝ I
V = RI
I = \(\frac { V }{ R }\)
R = \(\frac { V }{ I }\)
Where, R is constant for the given conductor at a given temperature and is called resistance.
Resistance: Resistance is the property of conductor which resists the flow of electric current through it.
S.I. unit of resistance is ohm. Ohm is denoted by Greek letter ‘Q’
1 Ohm: 1 ohm (Q) of resistance (R) is equal to the flow 1A of current through a conductor between two points having a potential difference equal to 1V.
This means; 1Ω = \(\frac { 1V }{ 1A }\)
From the expression of Ohm’s Law, it is obvious that electric current through a resistor is inversely proportional to resistance. This means electric current will decrease with an increase in resistance and vice versa. The graph of V (potential difference) versus I (electric current) is always a straight line.
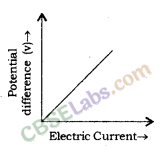
Graph of Potential Difference (V) Vs Electric Current (I)
Voltage, i.e. Potential diffrence (V) = ?
We know, from Ohm’s Law that,
R = \(\frac { V }{ I }\)
15 Ω = \(\frac { V }{ 15A }\)
V = 225V
Resistance: Resistance is a property of conductor due to which it resists the flow of electric current through it. A component that is used to resist the flow of electric current in a circuit is called a resistor.
In practical application, resistors are used to increase or decrease the electric current.
Variable Resistance: The component of an electric circuit which is used to regulate the current, without changing the voltage from the source, is called variable resistance.
Rheostat: This is a device which is used in a circuit to provide variable resistance.
Cause of Resistance in a Conductor: Flow of electrons in a conductor is electric current. The positive particles of conductor create hindrance to flow of electrons, because of attraction between them, this hindrance is the cause of resistance in the flow of electricity.
Factors on Which Resistance of a Conductor Depends: Resistance in a conductor depends on nature, length and area of cross section of the conductor.
(i) Nature of Material: Some materials create least hindrance and hence, are called good conductors. Silver is the best conductor of electricity. While some other materials create more hindrance in the flow of electric current, i.e. flow of electrons through them. Such materials are called bad conductors. Bad conductor are also known as insulators. Hard plastic is the one of the best insulators of electricity.
(ii) Length of Conductor: Resistance (R) is directly proportional to the length of the conductor. This means, resistance increases with increase in length of the conductor. This is the cause that long electric wires create more resistance to the electric current. Thus, Resistance (R) ∝ length of conductor (l)
or, R ∝ l …(i)
(iii) Area of Cross Section: Resistance R is inversely proportional to the area of cross section (A) of the conductor. This means R will decrease with an increase in the area of conductor and vice versa. More area of conductor facilitates the flow of electric current through more area and thus, decreases the resistance. This is the cause that thick copper wire creates less resistance to the electric current.
Thus, resistance (R) ∝ 1/Area of cross section of conductor (A)
or, R ∝ \(\frac { l }{ A }\) ….(ii)
From equations (i) and (ii)
R ∝ \(\frac { l }{ A }\)
R = ρ \(\frac { l }{ A }\)
Where, ρ (rho) is the proportionality constant. It is called the electrical resistivity of the material of conductor.
From equation (iii) RA = ρl ⇒ ρ = \(\frac { RA }{ l }\) ..(iv)
The S.I. of Resistivity: Since, the S.I. unit of R is Q, S.I. unit of area is m2 and S.I. unit of length is m. Hence, unit of resistivity (ρ) = \(\frac { \Omega \times { { m }^{ 2 } } }{ m }\) = Ωm
Thus, S.I. unit of resistivity (ρ) is Ωm.
Resistivity: It is defined as the resistance offered by a cube of a material of side 1m when current flows perpendicular to its opposite faces. It’s S.I. unit is ohm-meter (Ωm).
Resistivity, ρ = \(\frac { RA }{ l }\)
Resistivity is also known as specific resistance.
Resistivity depends on the nature of the material of the conductor.
Materials having a resistivity in the range of 10-8 Ωm to 10-6 Ωm are considered as very good conductors. Silver has resistivity equal to 1.60 × 10-8 Ωm and copper has resistivity equal to 1.62 × 10-8 Ωm.
Rubber and glass are very good insulators. They have a resistivity in the order of 10-12 Ωm to 10-8 Ωm.
The resistivity of materials varies with temperature.
Combination of resistors (Series and Parallel combination), the heating effect of electric current and electric power.
Combination of Resistors
(i) Series combination
(ii) Parallel combination.
1. Resistors in Series: When resistors are joined from end to end, it is called in series. In this case, the total resistance of the system is equal to the sum of the resistance of all the resistors in the system.
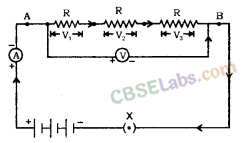
Let, three resistors R1, R2, and R3 get connected in series.
Potential difference across A and B = V
Potential difference across R1, R2 and R3 = V1, V2 and V3
Current flowing through the combination = I
We, know that
V= V1 + V2 + V3 …. (i)
According to Ohm’s Law :
V1 = IR1, V2 = IR2 and V3 = IR3 ….. (ii)
Let, total resistance = Rs
Then, V = IRs …(iii)
From equations (i) and (ii) and (iii)
IRs = IR1 + IR2 + IR3
Rs = R1 + R2 + R3
When the resistors are connected in series, the current flowing through each resistor is the same and is equal to the total current.
2. Resistors in Parallel: When resistors are joined in parallel, the reciprocal of the total resistance of the system is equal to the sum of reciprocal of the resistance of resistors.
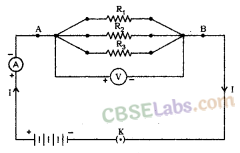
Let three resistors R1, R2 and R3 connected in parallel.
Potential difference across point A and B = V
Total current flowing between point A and B = I
Currents flowing through resistors R1, R2 and R3 = I1, I2 and I3 respectively.
We, know that,
I = I1 + I2 + I3 …….(i)
Since, the potential difference across R1, R2, and R3 is the same = V
According to Ohm’s Law,
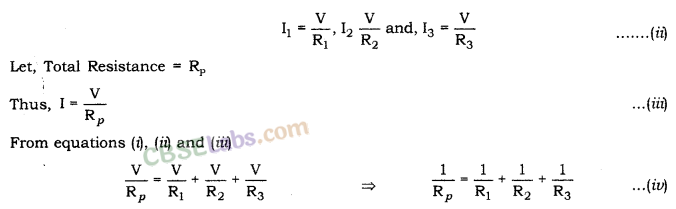
In parallel combination, the potential difference across each resistor is the same and is equal to the total potential difference.
The total current through the circuit can be calculated by adding the electric current through individual resistors.
Itotal = 6A + 48A + 30A + 12A + 24A = 120A
Heating Effect of Electric Current: When electric current is supplied to a purely resistive conductor, the energy of electric current is dissipated entirely in the form of heat and as a result, resistor gets heated. The heating of resistor because of dissipation of electrical energy is commonly known as Heating Effect of Electric Current. Some examples are as follows : When electric energy is supplied to an electric bulb, the filament gets heated because of which, it gives light. The heating of electric bulb happens because of heating effect of electric current.
Cause of Heating Effect of Electric Current: Electric current generates heat to overcome the resistance offered by the conductor through which it passes. Higher the resistance, the electric current will generate higher amount of heat. Thus, generation of heat by electric current while passing through a conductor is an inevitable consequence. This heating effect is used in many appliances, such as electric iron, electric heater, electric geyser, etc.
Joule’s Law Of Heating: Let, an electric current, I is flowing through a resistor having resistance = R.
The potential difference through the resistor is = V.
The charge, Q flows through the circuit for the time, t
Thus, work done in moving of charge (Q) of potential difference (V),
W = V × Q
Since this charge, Q flows through the circuit for time t
Therefore, power input (P) to the circuit can be given by the following equation :
P = \(\frac { W }{ T }\)
P = V × \(\frac { Q }{ t }\) …..(i)
We know, electric current, I = \(\frac { Q }{ t }\)
Substituting \(\frac { Q }{ t }\) = I in equation (i), we get,
P = VI …(ii)
i.e., P = VI
Since, the electric energy is supplied for time ?, thus, after multiplying both sides of equation (ii) by time t, we get,
P × t = VI × t = VIt ……(iii)
i.e., P = VIt
Thus, for steady current I, the heat produced (H) in time t is equal to VIt
H = VIt i.e., H = VIt
We know, according to Ohm’s Law,
V = IR
By substituting this value of V in equation (iii), we get,
H = IR × It
H = I2Rt ……(iv)
The expression (iv) is known as Joule’s Law of Heating, which states that heat produced in a resistor is directly proportional to the square of current given to the resistor, directly proportional to the resistance for a given current and directly proportional to the time for which the current is flowing through the resistor.
Electric Bulb: In an electric bulb, the filament of bulb gives light because of the heating effect of electricity. The filament of bulb is generally, made of tungsten metal, having melting point equal to 3380°C.
Electric Iron: The element of electric iron is made of alloys having high melting poir^ Electric heater and geyser work on the same mechanism.
Electric Fuse: Electric fuse is used to protect the electric appliances from high voltage if any. Electric fuse is made of metal or alloy of metals, such as aluminum, copper, iron, lead, etc. In the case of flow of higher voltage than specified, fuse wire melts and protect the electric appliances.
Fuse of 1A, 2A, 3A, 5A, 10A, etc., used for domestic purpose.
Suppose, if an electric heater consumes 1000W at 220 V.
Then electric current in circuit
I = \(\frac { P }{ V }\)
I = \(\frac { 1000W }{ 220V }\) = 4.5 A
Thus, in this case of 5A should be used to protect the electric heater in the flow of higher voltage.
Electric Power
S.I. unit of electric power is watt (W).
1W = 1 volt × 1 ampere = 1V × 1A
I kilowatt or 1kW = 1000 W
Consumption of electricity (electric energy) is generally measured in kilowatt.
Unit of electric energy is kilowatt-hour (kWh).
1 kWh = 1000 watt × 1 hour = 1 unit = 1000 W × 3600 s
1 kWh = 3.6 x 106 watt second = 3.6 × 106 J
Conductor: The material which can allow the flow of electrons through itself is called the conductor. It has a large number of free electrons. It offers low opposition in the flow of current.
Insulator: The material which does not allow the flow of electrons through itself is called insulator. It has less or no free electrons. It offers high opposition in the flow of current.
Electric Current: The amount of flow charge through any cross-sectional area of a conductor in unity time is called Electric Current.
It is represented by ‘I’
I = \(\frac { Q }{ T }\)
Unit of Electric Current: It is CS-1 (coulomb per second) or Ampere (A). Electric Current is a scalar quantity. It is measured by an ammeter.
Direction: The direction of conventional current (or practical current) is opposite to the flow of electrons.
Electric potential: Electric Potential at any point in the electric field is defined as the amount of work done to bring the unit positive charge from infinity (from outside the electric field) to that point.
V =\(\frac { W }{ Q }\), S.I. unit of Electric Potential is JC-1 or volt (V). It is a scalar quantity. The +ve charge flows from higher to lower potential. The -ve charge flows from lower to a higher potential. The difference of electric potential between any two points in the electric field is called Electric Potential difference. It is known as a voltage which is equal to the work done per unit charge between two points against the static electric field.
VAB = VA – VB = \(\frac { { W }_{ AB } }{ Q }\)
Electric Potential difference is measured by a voltmeter.
Ohm’s Law: According to this law “Under the constant physical condition the potential difference across the conductor is directly proportional to the current flowing through the conductor.”
V ∝ I
V = IR …[Where R is proportionality constant called resistance of conductor]
⇒ I = \(\frac { V }{ R }\)
R depends upon nature, geometry and physical condition of the conductor.
The heat generated by electric current: The potential difference between two points in an electrical field is equal to the work done in moving a unit charge from one point to another.
Then, work is done, W = VQ and Q = I × t
W = V × I × t
From Ohm’s Law, we know that
V = IR
W = IR × I × t = I2.Rt
Since heat produced by the electric current is equal to work done, W
H = W
⇒ H (heat) = I2Rt Joule.
Resistance: Ratio of the applied voltage to the current flowing in the conductor is called resistance of the conductor.
⇒ R = \(\frac { V }{ I }\)
S.I. Unit of resistance is VA-1 or ohm (Ω).
Resistance is the opposition offered by the conductor in the flow of current.
Practically it is
R ∝ L (L is the length of a conductor)
R ∝ 1/A (A is the area of a conductor)
So, R ∝ L/A
R = ρL/A …[Where p is proportionality constant called specific resistance of conductor
It only depend upon nature (material) and temperature of conductor.
Specific resistance or Resistivity = ρ = RA /L
It’s S.I. Unit is Qm
Combination of resistance:
- In this combination the current across every component is same but potential across every component is different.
- If resistance R1, R2 and R3 are connected in series with a battery of Potential V, then equivalence resistance of the combination
R = R1 + R2 + R3
The parallel combination of resistance:
- In this combination the current across every component is different. But potential across every component is the same.
- If resistance R1, R2 and R3 are connected in parallel with a battery of Potential V, then equivalence resistance of combination
\(\frac { 1 }{ R } =\frac { 1 }{ { R }_{ 1 } } +\frac { 1 }{ { R }_{ 2 } } +\frac { 1 }{ { R }_{ 3 } }\)
Electric Energy is amount of work done to maintain the continuous flow of electric current in the circuit.
Its S.I. unit is joule (J).
Electric power (P): The electric work done per unit time is called electric power.
Electric Power = \(\frac { Electric\quad work\quad done }{ Time\quad taken }\)
or P = \(\frac { W }{ t }\)
Electric power is also defined as the electric energy consumed per unit time.
P = \(\frac { E }{ t }\)
S.I. unit of electric power is Watt. When one joule of energy is used for one second, electric power is equal to one watt.
Derivation of formula for electric power:
We know that electric work done, W = V × I × t or P = \(\frac { VIt }{ t }\)
P = VI
Electric power in watts = Volts × ampere
Also V = IR …[According to Ohm’s Law]
So P = IR × I
P = I2R
We know that I = \(\frac { V }{ R }\)
P = (\(\frac { V }{ R }\))2 × R = \(\frac { { V }^{ 2 } }{ R }\) Watt
The maximum value of electric current that can pass through an electric appliance without damaging electric appliance is called current rating of electric appliance.
NCERT Notes for Class 10 Science
- Chapter 1 Chemical Reactions and Equations Class 10 Notes
- Chapter 2 Acids Bases and Salts Class 10 Notes
- Chapter 3 Metals and Non-metals Class 10 Notes
- Chapter 4 Carbon and its Compounds Class 10 Notes
- Chapter 5 Periodic Classification of Elements Class 10 Notes
- Chapter 6 Life Processes Class 10 Notes
- Chapter 7 Control and Coordination Class 10 Notes
- Chapter 8 How do Organisms Reproduce Class 10 Notes
- Chapter 9 Heredity and Evolution Class 10 Notes
- Chapter 10 Light Reflection and Refraction Class 10 Notes
- Chapter 11 Human Eye and Colourful World Class 10 Notes
- Chapter 12 Electricity Class 10 Notes
- Chapter 13 Magnetic Effects of Electric Current Class 10 Notes
- Chapter 14 Sources of Energy Class 10 Notes
- Chapter 15 Our Environment Class 10 Notes
- Chapter 16 Management of Natural Resources Class 10 Notes
We hope the given CBSE Class 10 Science Notes Chapter 12 Electricity Pdf free download will help you. If you have any query regarding NCERT Class 10 Science Notes Chapter 12 Electricity, drop a comment below and we will get back to you at the earliest.