RD Sharma class 10 solutions Chapter 8 Quadratic Equations Ex 8.2
RD Sharma Class 10 Solutions Quadratic Equations Exercise 8.2
Question 1.
The product of two consecutive positive integers is 306. Form the quadratic equation to find the integers, if x denotes the smaller integer. [NCERT]
Solution:
Let the first number = x
Then second number = x + 1
Their product = 306
x (x + 1) = 306
⇒ x2 + x – 306 = 0
Required quadratic equation will be x2 + x – 306 = 0
Question 2.
John and Jivanti together have 45 marbles. Both of them lost 5 marbles each, and the product of the number of marbles they now have is 128. Form the quadratic equation to find how many marbles they had to start with, if John had x marbles.
Solution:
No. of marbles John and Jivanti have = 45
Let number of marbles John has = x
Then number of marbles Jivanti has = 45 -x
Every one lost 5 marbles, then John’s marbles = x – 5
and Jivanti’s marbles = 45 – x – 5 = 40 – x
According to the condition,
(x – 5) (40 – x) = 128
⇒ 40x – x2 – 200 + 5x – 128 = 0
⇒ -x2 + 45x – 328 = 0
⇒ x2 – 45x + 328 = 0
Question 3.
A cottage industry produces a certain number of toys in a day. The cost of production of each toy (in rupees) was found to be 55 minus the number of articles produced in a day. On a particular day, the total cost of production was Rs. 750. If x denotes the number of toys produced that day, form the quadratic equation of find x.
Solution:
Let the number of toys in a day = x
Cost of each toy = x – 55
on a particular cost of production = Rs. 750
x (x – 55) = 750
⇒ x2 – 55x – 750 = 0
Hence required quadratic equation will be x2 – 55x – 750 = 0
Question 4.
The height of a right triangle is 7 cm less than its base. If the hypotenuse is 13 cm, form the quadratic equation to find the base of the triangle.
Solution:
Let the base of a right triangle = x
Its height = x – 7
and hypotenuse = 13 cm
⇒ By Pythagoras Theorem
(Hypotenuse)2 = (Base)2 + (Height)2
(13 )2 = x2 + (x – 7)2
⇒ 169 = x2 + x2 – 14x + 49
⇒ 2x2 – 14x + 49 – 169 = 0
⇒ 2x2 – 14x – 120 = 0
⇒ x2 – 7x – 60 = 0 (Dividing by 2)
Hence required quadratic equation will be x2 – 7x – 60 = 0
Question 5.
An express train takes 1 hour less than a passenger train to travel 132 km between Mysore and Bangalore. If the average speed of the express train is 11 km/hr more than that of the passenger train, form the quadratic equation to find the average speed of express train.
Solution:
Distance between Mysore and Bangalore = 132 km
Let average speed of passenger train=x km/ hr
Then average speed of express train = (x + 11) km/hr

Question 6.
A train travels 360 km at a uniform speed. If the speed had been 5 km/hr more, it would have taken 1 hour less for the same journey. Form the quadratic equation to find the speed of the train.
Solution:
Total distance = 360 km
Let the uniform speed of the train = x km/hr
Time taken = \(\frac { 360 }{ x }\)

Exercise 8.2





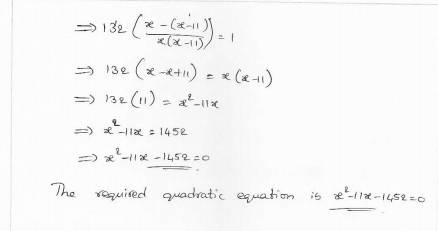


RD Sharma Class 10 Solutions
- Chapter 8 Quadratic Equations Ex 8.1
- Chapter 8 Quadratic Equations Ex 8.2
- Chapter 8 Quadratic Equations Ex 8.3
- Chapter 8 Quadratic Equations Ex 8.4
- Chapter 8 Quadratic Equations Ex 8.5
- Chapter 8 Quadratic Equations Ex 8.6
- Chapter 8 Quadratic Equations Ex 8.7
- Chapter 8 Quadratic Equations Ex 8.8
- Chapter 8 Quadratic Equations Ex 8.9
- Chapter 8 Quadratic Equations Ex 8.10
- Chapter 8 Quadratic Equations Ex 8.11
- Chapter 8 Quadratic Equations Ex 8.12
- Chapter 8 Quadratic Equations Ex 8.13