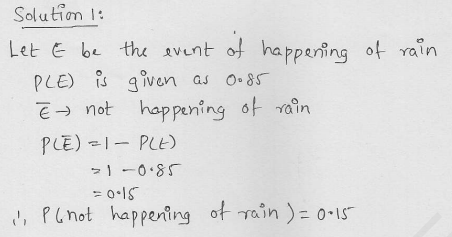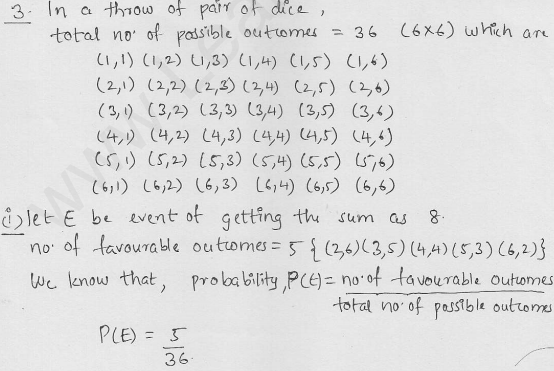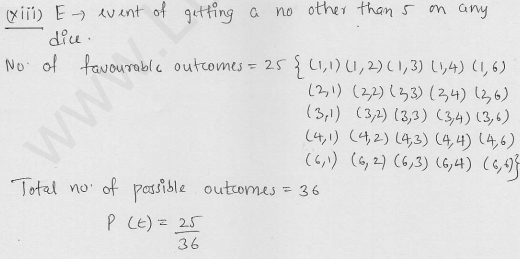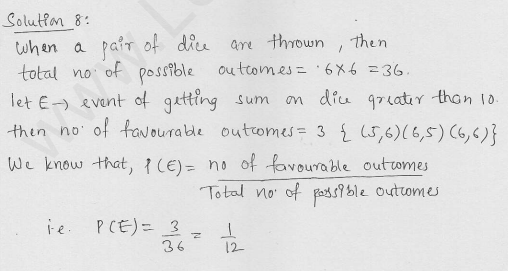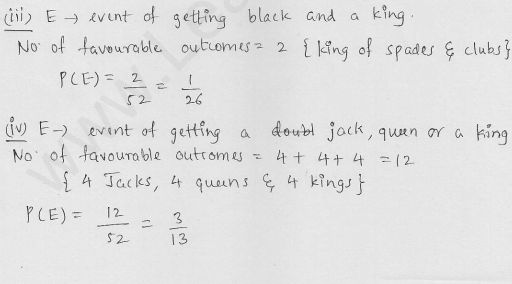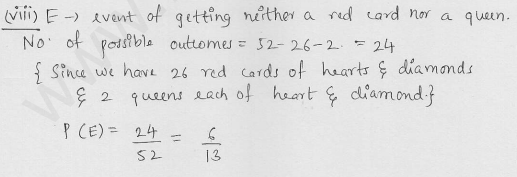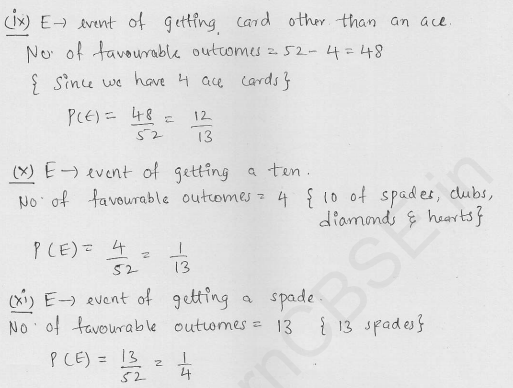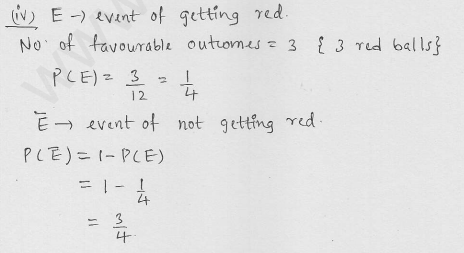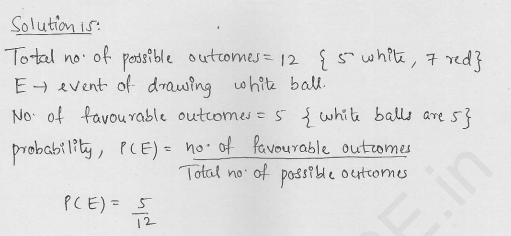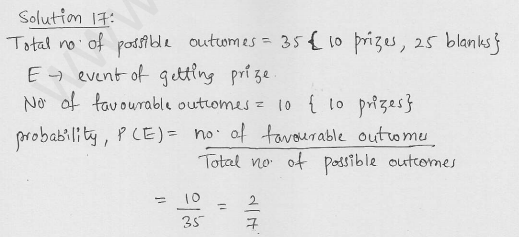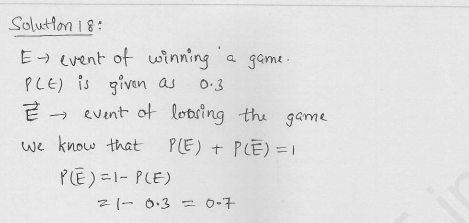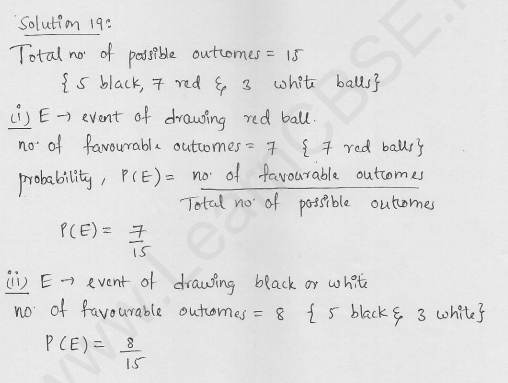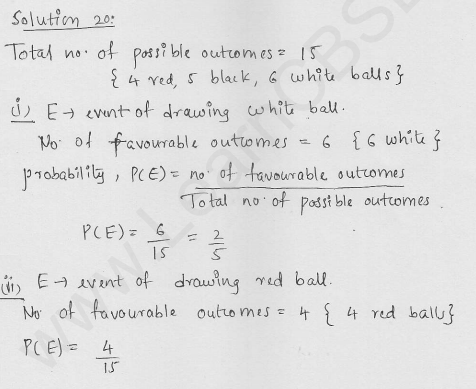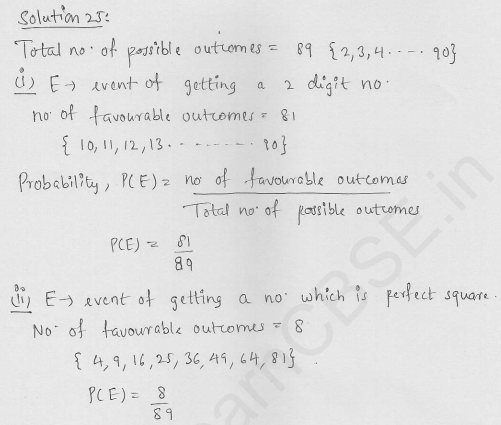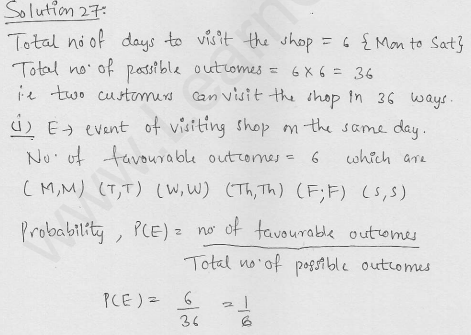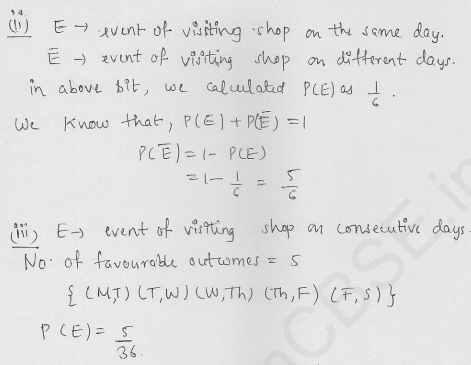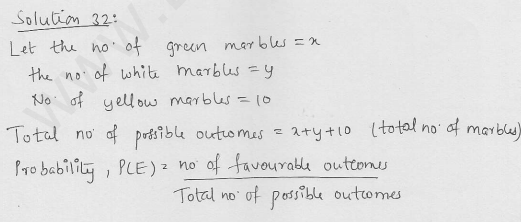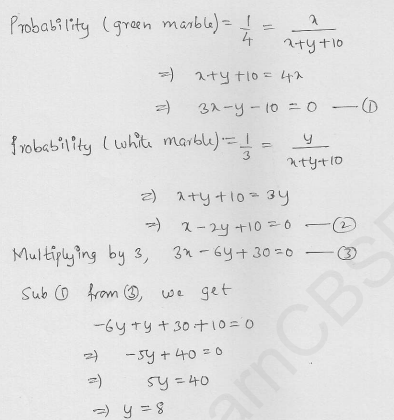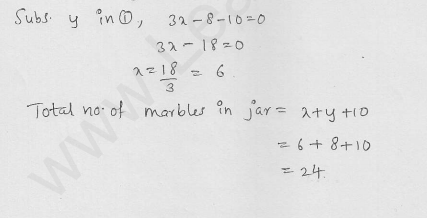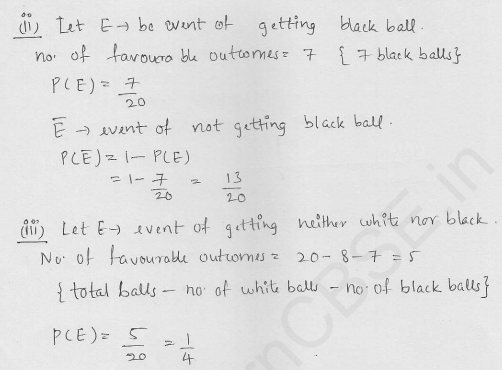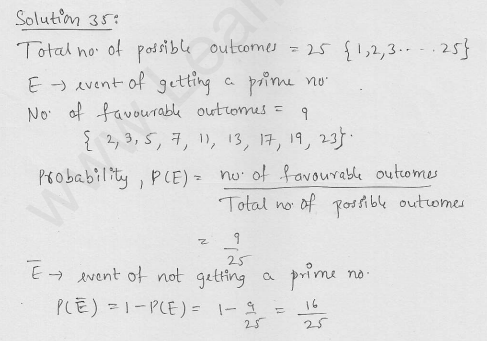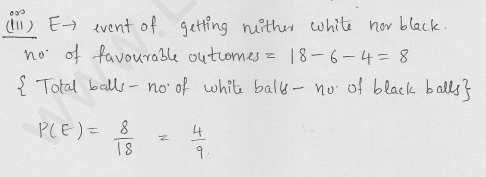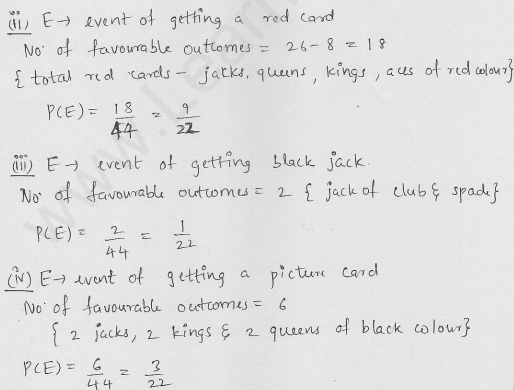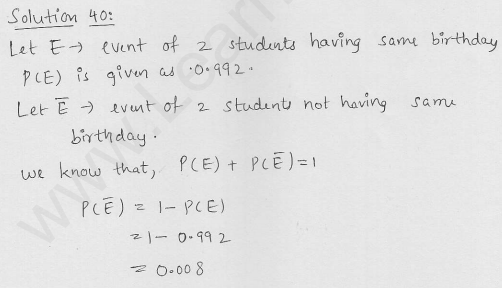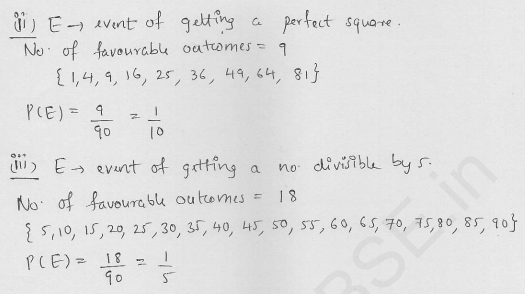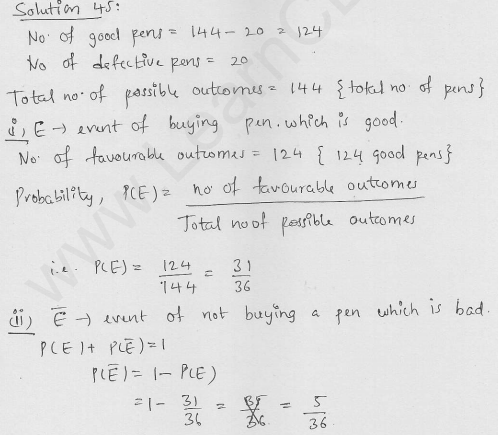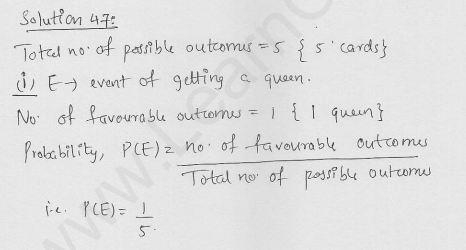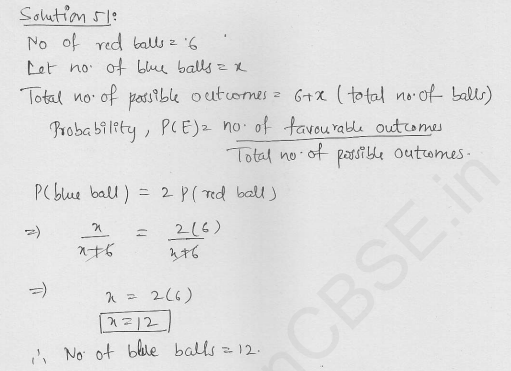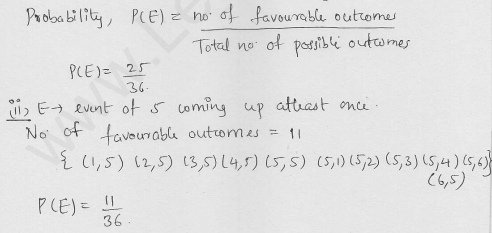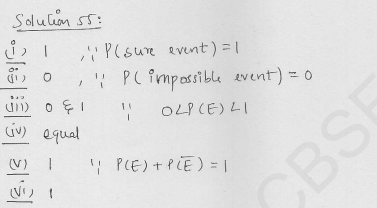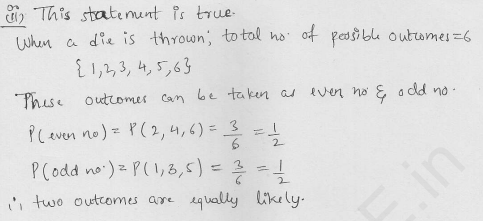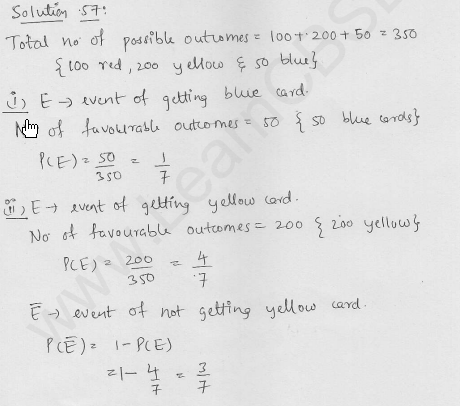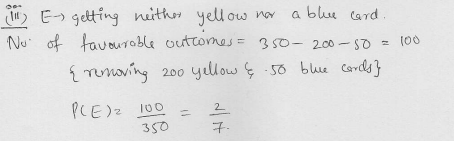RD Sharma Class 10 Solutions Chapter 13: Probability
RD Sharma Class 10 Solutions Probability Exercise 13.1
Question 1.
The probability that it will rain tomorrow is 0.85. What is the probability that it will not rain tomorrow ?
Solution:

Question 2.
A die is thrown. Find the probability of getting :
(i) a prime number
(ii) 2 or 4
(iii) a multiple of 2 or 3
(iv) an even prime number
(v) a number greater than 5 (CBSE 2008)
(vi) a number lying between 2 and 6 [NCERT]
Solution:

Question 3.
Three coins are tossed together. Find the probability of getting:
(i) exactly two heads
(ii) at most two heads
(iii) at least one head and one tail
(iv) no tails
Solution:

Question 4.
A and B throw a pair of dice. If A throws 9, find B’s chance of throwing a higher number.
Solution:

Question 5.
Two unbiased dice are thrown. Find the probability that the total of the numbers on the dice is greater than 10.
Solution:

Question 6.
A card is drawn at random from a pack of 52 cards. Find the probability that the card drawn is
(i) a black king
(ii) either a black card or a king
(iii) black and a king
(iv) a jack, queen or a king
(v) neither a heart nor a king
(vi) spade or an ace
(vii) neither an ace nor a king
(viii) neither a red card nor a queen [CBSE 2005]
(ix) other than an ace
(x) a ten
(xi) a spade
(xii) a black card
(xiii)the seven of clubs
(xiv) jack
(xv) the ace of spades
(xvi) a queen
(xvii) a heart
(xviii) a red card
(xix) neither a king nor a queen [CBSE 2013]
Solution:




Question 7.
In a lottery of 50 tickets numbered 1 to 50, one ticket is drawn. Find the probability that the drawn ticket bears a prime number.
Solution:

Question 8.
An urn contains 10 red and 8 white balls. One ball is drawn at random. Find the probability that the ball drawn is white.
Solution:

Question 9.
A bag contains 3 red balls, 5 black balls and 4 white balls. A ball is drawn at random from the bag. What is the probability that the ball drawn is:
(i) white?
(ii) red?
(iii) black?
(iv) not red? [CBSE2008]
Solution:

Question 10.
What is the probability that a number selected from the numbers 1, 2, 3…… 15 is a multiple of 4 ?
Solution:

Question 11.
A bag contains 6 red, 8 black and 4 white balls. A ball is drawn at random. What is the probability that ball drawn is not black?
Solution:

Question 12.
A bag contains 5 white and 7 red balls. One ball is drawn at random. What is the probability that ball drawn is white ?
Solution:

Question 13.
Tickets numbered from 1 to 20 are mixed up and a ticket is drawn at random. What is the probability that the ticket drawn has a number which is a multiple of 3 or 7?
Solution:

Question 14.
In a lottery there are 10 prizes and 25 blanks. What is the probability of getting a prize ?
Solution:

Question 15.
If the probability of winning a game is 0.3, what is the probability of loosing it ?
Solution:

Question 16.
A bag contains 5 black, 7 red and 3 white balls. A ball is drawn from the bag at random. Find the probability that the ball drawn is:
(i) red
(ii) black or white
(iii) not black
Solution:

Question 17.
A bag contains 4 red, 5 black and 6 white balls. A ball is drawn from the bag at random. Find the probability that the ball drawn is:
(i) white
(ii) red
(iii) not black
(iv) red or white [CBSE 2004]
Solution:

Question 18.
One card is drawn from a well shuffled deck of 52 cards. Find the probability of getting:
(i) a king of red suit
(ii) a face card
(iii) a red face card
(iv) a queen of black suit
(v) a jack of hearts
(vi) a spade [NCERT]
Solution:

Question 19.
Five cards ten, jack, queen, king and an ace of diamonds are shuffled face downwards. One card is picked at I j random.
(i) What is the probability that the card is a queen ?
(ii) If a king is drawn first and put aside, what is the probability that the second card picked up is the (i) ace (ii) king?
Solution:

Question 20.
A bag contains 3 red balls and 5 black balls. A ball is drawn at random from the bag. What is the probability that the ball drawn is:
(i) red
(ii) black
Solution:

Question 21.
A game of chance consists of spinning an arrow which is equally likely to come to rest pointing to one of the number, 1, 2, 3,………12 as shown in the figure. What is the probability that it will point to:

(i) 10?
(ii) an odd number?
(iii) a number which is multiple of 3?
(iv) an even number?

Question 22.
In a class, there are 18 girls and 16 boys. The class teacher wants to choose one pupil for class monitor. What she does, she writes the name of each pupil on a card and puts them into a basket and mixes thoroughly. A child is asked to pick one card from the basket. What is the probability that the name written on the card is: .
(i) the name of a girl
(ii) the name of a boy?
Solution:

Question 23.
Why is tossing a coin considered to be a fair way of deciding which team should choose ends in a game of cricket ?
Solution:
When we toss a coin, there are two outcomes of being a head and a tail equally So, the result of an individual coin toss is complelery are predictable. That is why, coin is tossed to decide which team should choose the end for the game
Question 24.
What is the probability that a number selected at random from the number 1, 2,2,3,3,3,4,4,4,4 will be their average?
Solution:

Question 25.
There are 30 cards, of same size, iiTa bag on which numbers 1 to 30 are written. One card is taken out of the bag at random. Find the probability that the number on the selected card is not divisible by 3. [CBSE 2005]
Solution:

Question 26.
A bag contains 5 red, 8 white and 7 black balls. A ball is drawn at random from the bag. Find the probability that the drawn ball is (i) red or white (ii) not black (iii) neither white nor black. [CBSE 2005]
Solution:

Question 27.
Find the probability that a number selected from a number 1 to 25 is not a prime number when each of the given numbers is equally likely to be selected. [CBSE 2005]
Solution:

Question 28.
A bag contains 8 red, 6 white and 4 black balls. A ball is drawn at random from the bag. Find the probability that the drawn ball is
(i) red or white
(ii) not black
(iii) neither white nor black.
Solution:

Question 29.
Find the probability that a number selected at random from the numbers 1, 2, 3,….. , 35 is a
(i) prime number
(ii) multiple of 7
(iii) a multiple of 3 or 5 [CBSE 2006C]
Solution:

Question 30.
From a pack of 52 playing cards Jacks, queens, kings and aces of red colour, are removed. From the remaining, a card is drawn at random. Find the probability that the card drawn is
(i) a black queen
(ii) a red card
(iii) a black jack
(iv) a picture card (Jacks, queens and kings are picture cards).
Solution:

Question 31.
A bag contains lemon flavoured candies only. Malini takes out one candy without looking into the bag. ‘What is the probability that she takes out
(i) an orange flavoured candy?
(ii) a lemon flavoured candy? [NCERT]
Solution:

Question 32.
It is given that in a group of 3 students, the probability of 2 students not having the same birthday is 0.992. What is the probability that the 2 students have the same birthday? [NCERT]
Solution:
n a group of 3 students, the probability of 2 students not having the same birthday=0.992 Probability of 2 students having the same birthday = 1 – 0.992 = 0.008
Question 33.
A bag contains 3 red balls and 5 black balls. A ball is drawn at random from the bag. What is the probability that the ball drawn is (i) red? (ii) not red?
Solution:

Question 34.
A box contains 5 red marbles, 8 white marbles and 4 green marbles. One marble is taken out of the box at random. What is the probability that the marble taken out will be (i) red? (ii) white? (iii) not green? [NCERT]
Solution:

Question 35.
A lot consists of 144 ball pens of which 20 are defective and others good. Nuri will buy a pen if it is good, but will not buy if it is defective. The shopkeeper draws one pen at random and gives it to her. What is the probability that
(i) She will buy it?
(ii) She will not buy it?
Solution:

Question 36.
12 defective pens are accidently mixed with 132 good ones. It is not possible to just look at pen and tell whether or not it is defective. One pen is taken out at random from this lot. Determine the probability that the pen taken out is good one.
Solution:

Question 37.
Five cards the ten, jack, queen, king and ace of diamonds, are well-shuffled with their face downwards. One card is then picked up at random.
(i) What is the probability that the card is the queen ?
(ii) If the queen is drawn and put a side, what is the probability that the second card picked up is (a) an ace? (b) a queen?
Solution:

Question 38.
Harpreet tosses two different coins simultaneously (say, one is of ₹1 and other of ₹2). What is the probability that the gets at least one head ?
Solution:

Question 39.
Cards marked with numbers 13, 14, 15,……. 60 are placed in a box and mixed thoroughly. One card is drawn at random from the box. Find the probability that, number on the card drawn is
(i) divisible by 5
(ii) a number is a perfect square [CBSE 2007]
Solution:

Question 40.
A bag contains tickets numbered 11, 12, 13,……..,30. A ticket is taken out from
the bag at random. Find the probability that the number on the drawn ticket
(i) is a multiple of 7
(ii) is greater than 15 and a multiple of 5. [CBSE 2008]
Solution:

Question 41.
Fill in the blanks :
(i) Probability of a sure event is …….
(ii) Probability of an impossible event is …….. .
(iii) The probability of an event (other than sure and impossible event) lies between …… .
(iv) Every elementary event associated to a random experiment has ……… probability.
(v) Probability of an event A + Probability of event ‘not A’ = …….. .
(vi) Sum of the probabilities of each outcome in an experiment is ……… .
Solution:
(i) Probability of a sure event is 1.
(ii) Probability of an impossible event is 0 (zero).
(iii) The probability of an event (other than sure and impossible event) lies between 0 and 1
i. e., 0 < probability <1.
(iv) Every elementary event associated to a random experiment has equal probability.
(v) Probability of an event A + Probability of event ‘not A’ = 1 (∵ \(\bar { A }\) + A = 1)
(vi) Sum of the probabilities of each outcome in an experiment is 1.
Question 42.
Examine each of the following statements and comment:
(i) If two coins are tossed at the same time, there are 3 possible outcomes two heads, two tails, or one of each. Therefore, for each outcome, the probability of occurrence is 1/3.
(ii) If a die is thrown once, there are two possible outcomes an odd number of an even number. Therefore, the probability of obtaining an odd number is 1/2 and the probability of obtaining an even number is 1/2.
Solution:

Question 43.
A box contains 100 red cards, 200 yellow cards and 50 blue cards. If a card is drawn at random from the box, then find the probability that it will be (i) a blue card (ii) not a yellow card (iii) neither yellow nor a blue card. [CBSE 2012]
Solution:

Question 44.
A box contains cards numbered 3,5,7,9, .., 35,37. A card is drawn at random from the box. Find te probability that the number on the drawn card is a prime number. [CBSE 2013]
Solution:

Question 45.
A group consists of 12 persons, of which 3 are extremely patient, other 6 are extremely honest and rest are extremely kind. A person from the group is selected at random. Assuming that each person is equally likely to be selected, find the probability of selecting a person who is (i) extremely patient (ii) extremely kind or honest. Which of the above you prefer more. [CBSE 2013]
Solution:

Question 46.
Cards numbered 1 to 30 are put in a bag. A card is drawn at random from this bag. Find the probability that the number on the drawn card is [CBSE 2014]
(i) not divisible by 3
(ii) a prime number great than 7
(iii) not a perfect square number.
Solution:

Question 47.
A piggy bank contains hundred 50 paise, fifty ₹1 coins, twenty ₹2 coins and ten ₹5 coins. If it is equally likely that one of the coins will fall out when the bank is turned upside down, find the probability that the coins which fell
(i) will be a 50 paise win
(ii) will be of value more than ₹1
(iii) will be of value less than ₹5
(iv) will be a ₹1 or ₹2 coins [CBSE 2014]
Solution:

Question 48.
A bag contains cards numbered from 1 to 49. A card is drawn from the bag at random, after mixing the card thoroughly. Find the probability that the number on the drawn card is
(i) an odd number
(ii) a multiple of 5
(iii) a perfect square
(iv) an even prime number. [CBSE 2014]
Solution:

Question 49.
A box contains 20 cards numbered from 1 to 20. A card is drawn at random from the box. Find the probability that the number on the drawn card is
(i) divisible by 2 or 3
(ii) a prime number [CBSE 2015]
Solution:

Question 50.
In a simultaneous throw of a pair of dice, find the probability of getting.
(i) 8 as the sum
(ii) a doublet
(iii) a doublet of prime numbers
(iv) a doublet of odd numbers
(v) a sum greater than 9
(vi) an even number on first
(vii) an even number on one and h multiple of 3 on the other
(viii)neither 9 nor 11 as the sum of the numbers on the faces
(ix) a sum less than 6
(x) a sum less than 7
(xi) a sum more than 7
(xii) at least once
(xiii)a number other than 5 on any dice.
(xiv) even number on each die [CBSE 2014,2015]
(xv) 5 as the sum [CBSE 2014,2015]
(xvi) 2 will come up at least once [CBSE 2015]
(xvii) 2 will not come either time [CBSE 2015]
Solution:




Question 51.
What is the probability that an ordinary year has 53 Sundays ?
Solution:

Question 52.
What is the probability that a leap year has 53 Sundays and 53 Mondays ?
Solution:

Question 53.
A black die and a white die are thrown at the same time. Write all the possible outcomes. What is the probability that :
(i) the sum of the two numbers that turn up is 8?
(ii) of obtaining a total of 6?
(iii) of obtaining a total of 10?
(iv) of obtaining the same number on both dice?
(v) of obtaining a total more than 9?
(vi) that the sum of the two numbers appearing on the top of the dice is 13?
(vii) that the sum of the numbers appearing on the top of the dice is less than or equal to 12?
(viii)that the product of numbers appearing on the top of the dice is less than 9.
(ix) that the difference of the numbers appearing on the top of the two dice is 2.
(x) that the numbers obtained have a product less than 16. [CBSE 2017]
Solution:

Question 54.
A bag contains cards which are numbered from 2 to 90. A card is drawn at random from the bag. Find the probability that it bears
(i) a two digit number
(ii) a number which is a perfect square.
Solution:

Question 55.
The faces of a red cube and a yellow cube are numbered from 1 to 6. Both cubes are rolled. What is the probability that the top face of each cube will have the same number ?
Solution:

Question 56.
The probability of selecting a green marble at random from a jar that contains only green, white and yellow marbles is 1/4. The probability of selecting a white marble at random from the same jar is 1/3. If this jar contains 10 yellow
marbles. What is the total number of marbles in the jar?
Solution:

Question 57.
(i) A lot of 20 bulbs contain 4 defective ones. One bulb is drawn at random from the lot. What is the probability that this bulb is defective?
(ii) Suppose the bulb drawn in (i) is not defective and not replaced. Now bulb is drawn at random from the rest. What is the probability that this bulb is not defective?
Solution:

Question 58.
A box contains 90 discs which are numbered from 1 to 90. If one discs is drawn at random from the box, find the probability that it bears
(i) a two digit number
(ii) a perfect square number
(iii) a number divisible by 5.
Solution:

Question 59.
Two dice, one blue and one grey, are thrown at the same time. Complete the following table:

From the above table a student argues that there are 11 possible outcomes 2, 3, 4, 5, 6, 7, 8, 9, 10,11 and 12. Therefore, each of them has a probability \(\frac { 1 }{ 11 }\). Do you agree with this
argument ?
Solution:


Question 60.
A bag contains 6 red balls and some blue balls. If the probability of drawing a blue ball from the bag is twice that of a red ball, find the number of blue balls in the bag.
[CBSE 2007]
Solution:

Question 61.
The king, queen and jack of clubs are removed from a deck of 52 playing cards and the remaining cards are shuffled. A card is drawn from the remaining cards. Find the probability of getting a card of (i) heart (ii) queen (iii) clubs (iv) a face card (v) a queen of diamond.
Solution:

Question 62.
Two dice are thrown simultaneously. What is the probability that :
(i) 5 will not come up on either of them ?
(ii) 5 will come up on at least one ?
(iii) 5 will come up at both dice? [CBSE 2009]
Solution:

Question 63.
A number is selected at random from first 50 natural numbers. Find the probability that it is a multiple of 3 and 4.
Solution:

Question 64.
A dice is rolled twice. Find the probability that
(i) 5 will not come up either time.
(ii) 5 will come up exactly one time. [CBSE 2014]
Solution:

Question 65.
All the black face cards are removed from a pack of 52 cards. The remaining cards are well shuffled and then a card is drawn at random. Find the probability to getting a
(i) face card
(ii) red card
(iii) black card
(iv) king.
Solution:

Question 66.
Cards numbered from 11 to 60 are kept in a box. If a card is drawn at random from the box, find the probability that the number on the drawn cards is
(i) an odd number
(ii) a perfect square number
(iii) divisible by 5
(iv) a prime number less than 20. [CBSE 2014]
Solution:

Question 67.
All kings and queens are removed from a pack of 52 cards. The remaining cards are well-shuffled and then a card is randomly drawn from it. Find the probability that this card is
(i) a red face card
(ii) a black card. [CBSE 2014]
Solution:

Question 68.
All jacks, queens and kings are removed from a pack of 52 cards. The remaining cards are well-shuffled and then a card is randomly drawn from it. Find the probability that this cards is
(i) a black face card
(ii) a red card. [CBSE 2014]
Solution:

Question 69.
Red queens and blackjacks are removed from a pack of 52 playing cards. A cards is drawn at random from the remaining cards, after reshuffling them. Find the probability that the card drawn is
(i) a king
(ii) of red colour
(iii) a face card
(iv) a queen [CBSE 2014]
Solution:

Question 70.
In a bag there are 44 identical cards with figure of circle or square on them. There are 24 circles, of which 9 are blue and rest are green and 20 squares of which 11 are blue and rest are green. One card is drawn from the bag at random. Find the probability that it has the figure of (i) square (ii) green colour, (iii) blue circle and (iv) green square. [CBSE 2015]
Solution:

Question 71.
All red face cards are removed from a pack of playing cards. The remaining cards are well shuffled and then a card is drawn at random from them. Find the probability that the drawn card is (i) a red card, (ii) a face card and (ii) a card of clubs. [CBSE 2015]
Solution:

Question 72.
Two customers are visiting a particular shop in the same week (Monday to Saturday). Each is equally likely to visit the shop on any one day as on another. What is the probability that both will visit the shop on:
(i) the same day?
(ii) different days?
(iii) consecutive days?
Solution:

Exercise 13.1
RD Sharma Class 10 Solutions
Summary:
- We find the probability of the occurrence of an event by actually performing the experiment a number of times and adequate recording of the happening of event.
- An Outcome of a random experiment is called an elementary event.
- Probability of an event E, written as P(E), is defined as \(P(E)=\frac { Number\quad of\quad outcomes\quad favourable\quad to\quad E }{ Number\quad of\quad all\quad possible\quad outcomes\quad of\quad the\quad experiment } \)
- An event associated to random experiment is a compound event if it is obtained by combining two or more elementary events associated to the random experiment.
- An event having only one outcome is called an elementary event. The sum of the probabilities of all the elementary events of an experiment is 1.
- The probability of a sure event (or certain event) is 1.
- The probability of an impossible event is 0
- The probability of an event E is a number P(E) such that \(0\le P(E)\le 1\)
- For any event E, \(P(E)+P(\overline { E } )=1 \), where \(\overline { E } \) stands for ‘not E’. E and \(\overline { E } \) are called complementary events.
RD Sharma Class 10 Solutions Probability Exercise 13.1
Q1 Q2 Q3 Q4 Q5 Q6 Q7 Q8 Q9 Q10 Q11 Q12 Q13 Q14 Q15 Q16 Q17 Q18 Q19 Q20 Q21 Q22 Q23 Q24 Q25 Q26 Q27 Q28 Q29 Q30 Q31 Q32 Q33 Q34 Q35 Q36 Q37 Q38 Q39 Q40 Q41 Q42 Q43 Q44 Q45 Q46 Q47 Q48 Q49 Q50 Q51 Q52 Q53 Q54 Q55 Q56 Q57 Q58
RD Sharma Class 10 Solutions Exercise 13.2
More Resources For Class 10
RD Sharma Class 10 SolutionsProbabilityClass 10 Maths Sample Papers