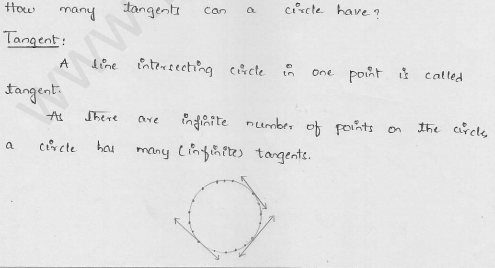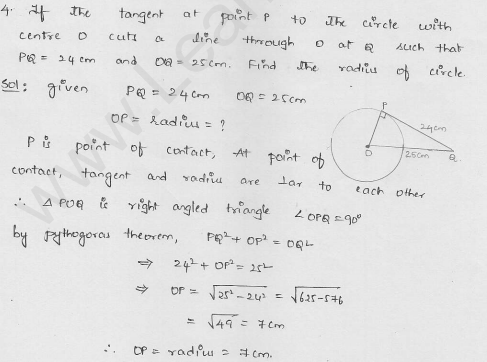RD Sharma Class 10 Solutions Chapter 10 Circles Ex 10.1
RD Sharma Class 10 Solutions Circles Exercise 10.1
Question 1.
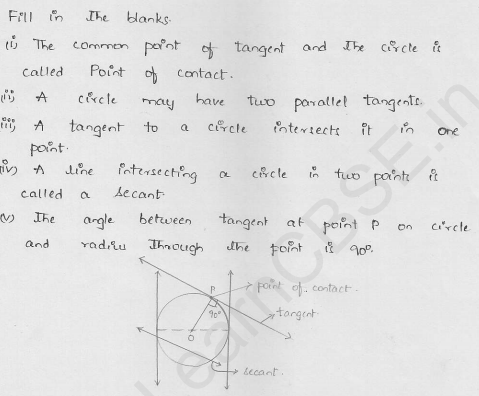
Fill in the blanks :
(i) The common point of a tangent and the circle is called ……….
(ii) A circle may have ………. parallel tangents.
(iii) A tangent to a circle intersects it in ……….. point(s).
(iv) A line intersecting a circle in two points is called a …………
(v) The angle between tangent at a point on a circle and the radius through the point is ………..
Solution:
(i) The common point of a tangent and the circle is called the point of contact.
(ii) A circle may have two parallel tangents.
(iii) A tangents to a circle intersects it in one point.
(iv) A line intersecting a circle in two points is called a secant.
(v) The angle between tangent at a point, on a circle and the radius through the point is 90°.
Question 2.
How many tangents can a circle have ?
Solution:
A circle can have infinitely many tangents.
Question 3.
O is the centre of a circle of radius 8 cm. The tangent at a point A on the circle cuts a line through O at B such that AB = 15 cm. Find OB.
Solution:
Radius OA = 8 cm, ST is the tangent to the circle at A and AB = 15 cm

OA ⊥ tangent TS
In right ∆OAB,
OB² = OA² + AB² (Pythagoras Theorem)
= (8)² + (15)² = 64 + 225 = 289 = (17)²
OB = 17 cm
Question 4.
If the tangent at a point P to a circle with centre O cuts a line through O at Q such that PQ = 24 cm and OQ = 25 cm. Find the radius of the circle.
Solution:
OP is the radius and TS is the tangent to the circle at P

OQ is a line
OP ⊥ tangent TS
In right ∆OPQ,
OQ² = OP² + PQ² (Pythagoras Theorem)
=> (25)² = OP² + (24)²
=> 625 = OP² + 576
=> OP² = 625 – 576 = 49
=> OP² = (7)²
OP = 7 cm
Hence radius of the circle is 7 cm