NCERT Solutions for Class 9 Maths Chapter 10 Circles Ex 10.6
The topics and sub-topics in NCERT Class 9 Maths Textbook Chapter 10 Circles:
- Circles
- Introduction
- Circles And Its Related Terms: A Review
- Angle Subtended By A Chord At A Point
- Perpendicular From The Centre To A Chord
- Circle Through Three Points
- Equal Chords And Their Distances From The Centre
- Angle Subtended By An Arc Of A Circle
- Cyclic Quadrilaterals
- Summary
Formulae Handbook for Class 9 Maths and Science Educational Loans in India
- Class 9 Maths Chapter 10 Circles NCERT Solutions Ex 10.1
- Class 9 Maths Chapter 10 Circles NCERT Solutions Ex 10.2
- Class 9 Maths Chapter 10 Circles NCERT Solutions Ex 10.3
- Class 9 Maths Chapter 10 Circles NCERT Solutions Ex 10.4
- Class 9 Maths Chapter 10 Circles NCERT Solutions Ex 10.5
- Extra Questions for Circles
NCERT Solutions for Class 9 Maths Chapter 10 Circles Ex 10.6
Ex 10.6 Class 9 Maths Question 1.
Prove that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.
Solution:
Given: Two circles with centres O and O’ which intersect each other at C and D.
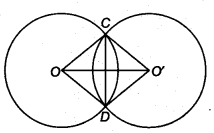
To prove: ∠OCO’ = ∠ODO’
Construction: Join OC, OD, O’C and O’D
Proof: In ∆ OCO’and ∆ODO’, we have
OC = OD (Radii of the same circle)
O’C = O’D (Radii of the same circle)
OO’ = OO’ (Common)
∴ By SSS criterion, we get
∆ OCO’ ≅ ∆ ODO’
Hence, ∠OCO’ = ∠ODO’ (By CPCT)
Ex 10.6 Class 9 Maths Question 2.
Two chords AB and CD of lengths 5 cm and 11 cm, respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle.
Solution:
Let O be the centre of the given circle and let its radius be cm.
Draw ON ⊥ AB and OM⊥ CD since, ON ⊥ AB, OM ⊥ CD and AB || CD, therefore points N, O, M are collinear.
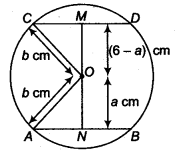
Let ON = a cm
∴ OM = (6 – a) cm
Join OA and OC.
Then, OA = OC = b c m
Since, the perpendicular from the centre to a chord of the circle bisects the chord.
Therefore, AN = NB= 2.5 cm and OM = MD = 5.5 cm
In ∆OAN and ∆OCM, we get
OA2 = ON2 + AN2
OC2 = OM2 + CM2
⇒ b2 = a2 + (2.5)2
and, b2 = (6-a)2 + (5.5)2 …(i)
So, a2 + (2.5)2 = (6 – a)2 + (5.5)2
⇒ a2 + 6.25= 36-12a + a2 + 30.25
⇒ 12a = 60
⇒ a = 5
On putting a = 5 in Eq. (i), we get
b2 = (5)2 + (2.5)2
= 25 + 6.25 = 31.25
So, r = \( \sqrt{31.25} \) = 5.6cm (Approx.)
Ex 10.6 Class 9 Maths Question 3.
The lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at distance 4 cm from the centre, what is the distance of the other chord from the centre ?
Solution:
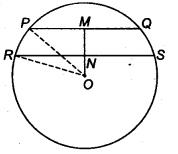
Let PQ and RS be two parallel chords of a circle with centre O such that PQ = 6 cm and RS = 8 cm.
Let a be the radius of circle.
Draw ON ⊥ RS, OM ⊥ PQ. Since, PQ || RS and ON ⊥ RS, OM⊥ PQ, therefore points 0,N,M are collinear.
∵ OM = 4 cm and M and N are the mid-points of PQ and RS respectively.
PM = MQ = \(\frac { 1 }{ 2 }\) PQ = \(\frac { 6 }{ 2 }\) = 3 cm
and RN = NS = \(\frac { 1 }{ 2 }\) RS = \(\frac { 8 }{ 2 }\) = 4 cm
In ∆OPM, we have
OP2 = OM2 + PM2
⇒ a2 =42 + 32 = 16 + 9 = 25
⇒ a = 5
In ∆ORN, we have
⇒ OR2 = ON2 + RN2
⇒ a2 = ON2 + (4)2
⇒ 25 = ON2 + 16
⇒ ON2 = 9
⇒ ON = 3cm
Hence, the distance of the chord PS from the centre is 3 cm.
Ex 10.6 Class 9 Maths Question 4.
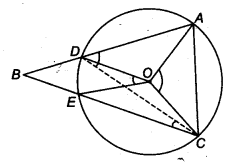
Let the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that ∠ABC is equal to half the difference of the angles subtended by the chords AC and DE at the centre.
Solution:
Since, an exterior angle of a triangle is equal to the sum of the interior opposite angles.
∴ In ∆BDC, we get
∠ADC = ∠DBC + ∠DCB …(i)
Since, angle at the centre is twice at a point on the remaining part of circle.
∴ ∠DCE = \(\frac { 1 }{ 2 }\) ∠DOE
⇒ ∠DCB = \(\frac { 1 }{ 2 }\) ∠DOE (∵ ∠DCE = ∠DCB)
∠ADC = \(\frac { 1 }{ 2 }\) ∠AOC
∴ \(\frac { 1 }{ 2 }\) ∠AOC = ∠ABC + \(\frac { 1 }{ 2 }\) ∠DOE (∵ ∠DBC = ∠ABC)
∴ ∠ABC = \(\frac { 1 }{ 2 }\) (∠AOC – ∠DOE)
Hence, ∠ABC is equal to half the difference of angles subtended by the chords AC and DE at the centre.
Ex 10.6 Class 9 Maths Question 5.
Prove that the circle drawn with any side of a rhombus as diameter, passes through the point of intersection of its diagonals.
Solution:
Given: PQRS is a rhombus. PR and SQ are its two diagonals which bisect each other at right angles.
To prove: A circle drawn on PQ as diameter will pass through O.
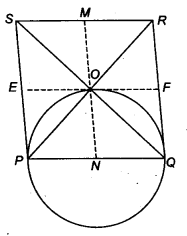
Construction: Through O, draw MN || PS and EF || PQ.
Proof : ∵ PQ = SR ⇒ \(\frac { 1 }{ 2 }\) PQ = \(\frac { 1 }{ 2 }\) SR
So, PN = SM
Similarly, PE = ON
So, PN = ON = NQ
Therefore, a circle drawn with N as centre and radius PN passes through P, O, Q.
Ex 10.6 Class 9 Maths Question 6.
ABCD is a parallelogram. The circle through A, B and C intersect CD (produced if necessary) at E. Prove that AE = AD.
Solution:
Since, ABCE is a cyclic quadrilateral, therefore
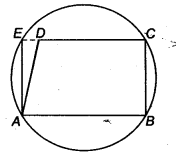
∠AED+ ∠ABC= 180°
(∵ Sum of opposite angle of a cyclic quadrilateral is 180°) .. .(i)
∵ ∠ADE + ∠ADC = 180° (EDC is a straight line)
So, ∠ADE + ∠ABC = 180°
(∵ ∠ADC = ∠ABC opposite angle of a || gm).. .(ii)
From Eqs. (i) and (ii), we get
∠AED + ∠ABC = ∠ADE + ∠ABC
⇒ ∠AED = ∠ADE
∴ In ∆AED We have
∠AED = ∠ADE
So, AD = AE
(∵ Sides opposite to equal angles of a triangle are equal)
Ex 10.6 Class 9 Maths Question 7.
AC and BD are chords of a circle which bisect each other. Prove that
(i) AC and BD are diameters,
(ii) ABCD is a rectangle.
Solution:
(i) Let BD and AC be two chords of a circle bisect at P.
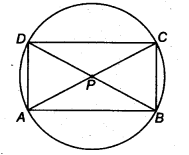
In ∆APB and ∆CPD, we get
PA = PC ( ∵ P is the mid-point of AC)
∠APB = ∠CPD (Vertically opposite angles)
and PB = PD (∵ P is the mid-point of BD)
∴ By SAS criterion
∆CPD ≅ ∆APB
∴ CD= AB (By CPCT) …(i)
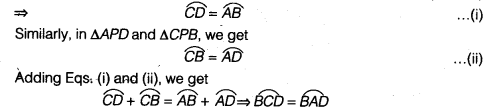
∴ BD divides the circle into two equal parts. So, BD is a diameter.
Similarly, AC is a diameter.
(ii) Now, BD and AC bisect each other.
So, ABCD is a parallelogram.
Also, AC = BD
∴ ABCD is a rectangle.
Ex 10.6 Class 9 Maths Question 8.
Bisectors of angles A, B and C of a ∆ABC intersect its circumcircle at D, E and F, respectively. Prove that the angles of the ∆DEF are 90° – \(\frac { 1 }{ 2 }\) A, 90° – \(\frac { 1 }{ 2 }\) B and 90° – \(\frac { 1 }{ 2 }\) C.
Solution:
∵ ∠EDF = ∠EDA + ∠ADF
∵ ∠EDA and ∠EBA are the angles in the same segment of the circle.
∴ ∠EDA = ∠EBA
and similarly ∠ADF and ∠FCA are the angles in the same segment and hence
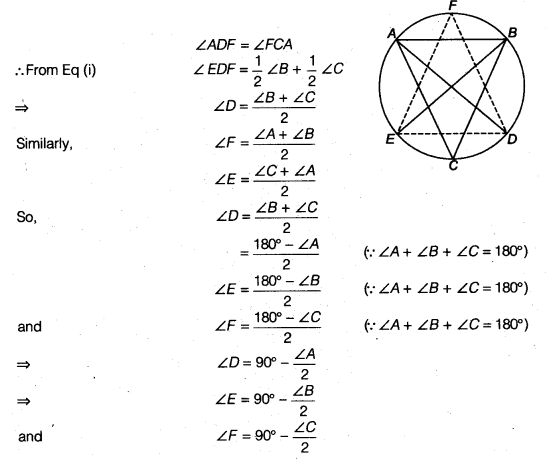
Ex 10.6 Class 9 Maths Question 9.
Two congruent circles intersect each other at points A and B. Through A any line segment PAQ is drawn so that P, Q lie on the two circles. Prove that BP = BQ.
Solution:
Let O’ and O be the centres of two congruent circles.
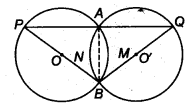
Since, AB is a common chord of these circles.
∴ ∠BPA = ∠BQA
(∵ Angle subtended by equal chords are equal)
⇒ BP = BQ
Ex 10.6 Class 9 Maths Question 10.
In any ∆ ABC, if the angle bisector of ∠A and perpendicular bisector of BC intersect, prove that they intersect on the circumcircle of the ∆ABC.
Solution:
(i) Let bisector of ∠A meet the circumcircle of ∆ABC at M.
Join BM and CM.
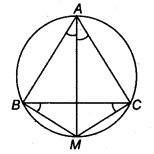
∴ ∠MBC = ∠MAC (Angles in same segment)
and ∠BCM = ∠BAM (Angles in same segment)
But ∠BAM = ∠CAM (∵ AM is bisector of ∠A)…. .(i)
∴ ∠MBC = ∠BCM
So, MB = MC (Sides opposite to equal angles are equal)
So, M must lie on the perpendicular bisector of BC
(ii) Let M be a point on the perpendicular bisector of BC which lies on circumcircle of ∆ ABC.
Join AM.
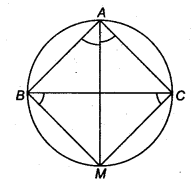
Since, M lies on perpendicular bisector of BC.
∴ BM = CM
∠MBC = ∠MCB
But ∠MBC = ∠MAC (Angles in same segment)
and ∠MCB = ∠BAM (Angles in same segment)
So, from Eq. (i),
∠BAM = ∠CAM
AM is the bisector of A.
Hence, bisector of ∠A and perpendicular bisector of BC at M which lies on circumcircle of ∆ABC.
NCERT Solutions for Class 9 Maths Chapter 10 Circles (वृत्त) (Hindi Medium) Ex 10.6














NCERT Solutions for Class 9 Maths
- Chapter 1 Number systems
- Chapter 2 Polynomials
- Chapter 3 Coordinate Geometry
- Chapter 4 Linear Equations in Two Variables
- Chapter 5 Introduction to Euclid Geometry
- Chapter 6 Lines and Angles
- Chapter 7 Triangles
- Chapter 8 Quadrilaterals
- Chapter 9 Areas of Parallelograms and Triangles
- Chapter 10 Circles
- Chapter 11 Constructions
- Chapter 12 Heron’s Formula
- Chapter 13 Surface Areas and Volumes
- Chapter 14 Statistics
- Chapter 15 Probability
- Class 9 Maths (Download PDF)