NCERT Solutions for Class 8 Maths Chapter 6 Squares and Square Roots Ex 6.2
- Class 8 Maths Squares and Square Roots Exercise 6.1
- Class 8 Maths Squares and Square Roots Exercise 6.2
- Class 8 Maths Squares and Square Roots Exercise 6.3
- Class 8 Maths Squares and Square Roots Exercise 6.4
- Squares and Square Roots Class 8 Extra Questions
NCERT Solutions for Class 8 Maths Chapter 6 Squares and Square Roots Exercise 6.2
Ex 6.2 Class 8 Maths Question 1.
Find the square of the following numbers.
(i) 32
(ii) 35
(iii) 86
(iv) 93
(v) 71
(vi) 46
Solution:
(i) 32 = 30 + 2
(32)2 = (30 + 2)2
= 30(30 + 2) + 2(30 + 2)
= 302 + 30 × 2 + 2 × 30 + 22
= 900 + 60 + 60 + 4
= 1024
Thus (32)2 = 1024
(ii) 35 = (30 + 5)
(35)2 = (30 + 5)2
= 30(30 + 5) + 5(30 + 5)
= (30)2 + 30 × 5 + 5 × 30 + (5)2
= 900 + 150 + 150 + 25
= 1225
Thus (35)2 = 1225
(iii) 86 = (80 + 6)
862 = (80 + 6)2
= 80(80 + 6) + 6(80 + 6)
= (80)2 + 80 × 6 + 6 × 80 + (6)2
= 6400 + 480 + 480 + 36
= 7396
Thus (86)2 = 7396
(iv) 93 = (90+ 3)
932 = (90 + 3)2
= 90 (90 + 3) + 3(90 + 3)
= (90)2 + 90 × 3 + 3 × 90 + (3)2
= 8100 + 270 + 270 + 9
= 8649
Thus (93)2 = 8649
(v) 71 = (70 + 1)
712 = (70 + 1)2
= 70 (70 + 1) + 1(70 + 1)
= (70)2 + 70 × 1 + 1 × 70 + (1)2
= 4900 + 70 + 70 + 1
= 5041
Thus (71)2 = 5041
(vi) 46 = (40+ 6)
462 = (40 + 6)2
= 40 (40 + 6) + 6(40 + 6)
= (40)2 + 40 × 6 + 6 × 40 + (6)2
= 1600 + 240 + 240 + 36
= 2116
Thus (46)2 = 2116
Ex 6.2 Class 8 Maths Question 2.
Write a Pythagorean triplet whose one member is
(i) 6
(ii) 14
(iii) 16
(iv) 18
Solution:
(i) Let m2 – 1 = 6
[Triplets are in the form 2m, m2 – 1, m2 + 1]
m2 = 6 + 1 = 7
So, the value of m will not be an integer.
Now, let us try for m2 + 1 = 6
⇒ m2 = 6 – 1 = 5
Also, the value of m will not be an integer.
Now we let 2m = 6 ⇒ m = 3 which is an integer.
Other members are:
m2 – 1 = 32 – 1 = 8 and m2 + 1 = 32 + 1 = 10
Hence, the required triplets are 6, 8 and 10
(ii) Let m2 – 1 = 14 ⇒ m2 = 1 + 14 = 15
The value of m will not be an integer.
Now take 2m = 14 ⇒ m = 7 which is an integer.
The member of triplets are 2m = 2 × 7 = 14
m2 – 1 = (7)2 – 1 = 49 – 1 = 48
and m2 + 1 = (7)2 + 1 = 49 + 1 = 50
i.e., (14, 48, 50)
(iii) Let 2m = 16 m = 8
The required triplets are 2m = 2 × 8 = 16
m2 – 1 = (8)2 – 1 = 64 – 1 = 63
m2 + 1 = (8)2 + 1 = 64 + 1 = 65
i.e., (16, 63, 65)
(iv) Let 2m = 18 ⇒ m = 9
Required triplets are:
2m = 2 × 9 = 18
m2 – 1 = (9)2 – 1 = 81 – 1 = 80
and m2 + 1 = (9)2 + 1 = 81 + 1 = 82
i.e., (18, 80, 82)

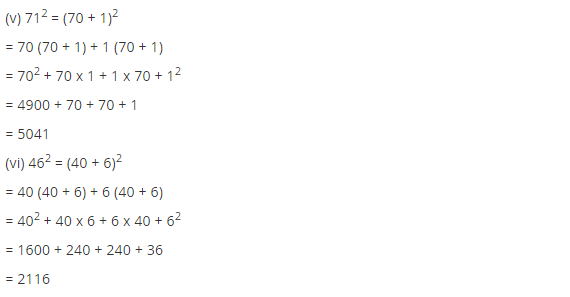

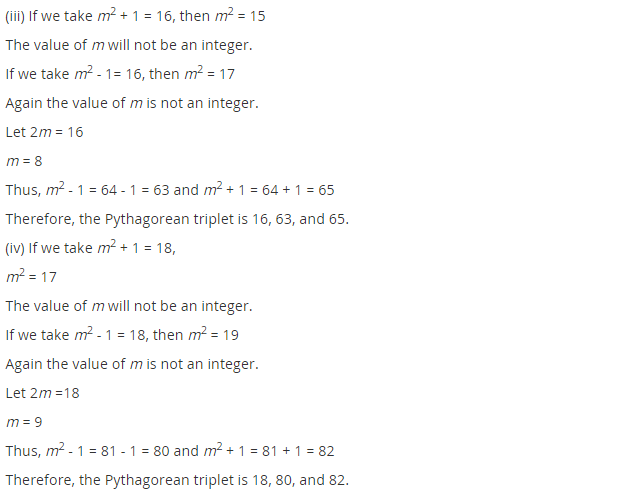
More CBSE Class 8 Study Material
- NCERT Solutions for Class 8 Maths
- NCERT Solutions for Class 8 Science
- NCERT Solutions for Class 8 Social Science
- NCERT Solutions for Class 8 English
- NCERT Solutions for Class 8 English Honeydew
- NCERT Solutions for Class 8 English It So Happened
- NCERT Solutions for Class 8 Hindi
- NCERT Solutions for Class 8 Sanskrit
- NCERT Solutions