NCERT Solutions for Class 8 Maths Chapter 14 Factorisation
- Class 8 Maths Factorisation Exercise 14.1
- Class 8 Maths Factorisation Exercise 14.2
- Class 8 Maths Factorisation Exercise 14.3
- Factorisation Class 8 Extra Questions
NCERT Solutions for Class 8 Maths Chapter 14 Factorisation Exercise 14.1
Ex 14.1 Class 8 Maths Question 1.
Find the common factors of the given terms.
(i) 12x, 36
(ii) 2y, 22xy
(iii) 14pq, 28p2q2
(iv) 2x, 3x2, 4
(v) 6abc, 24ab2, 12a2b
(vi) 16x3, -4x2, 32x
(vii) 10pq, 20qr, 30rp
(viii) 3x2y3, 10x3y2, 6x2y2z
Solution:
(i) 12x, 36
(2 × 2 × 3 × x) and (2 × 2 × 3 × 3)
Common factors are 2 × 2 × 3 = 12
Hence, the common factor = 12
(ii) 2y, 22xy
= (2 × y) and (2 × 11 × x × y)
Common factors are 2 × y = 2y
Hence, the common factor = 2y
(iii) 14pq, 28p2q2
= (2 × 7 × p × q) and (2 × 2 × 7 × p × p × q × q)
Common factors are 2 × 7 × p × q = 14pq
Hence, the common factor = 14pq
(iv) 2x, 3x2, 4
= (2 × x), (3 × x × x) and (2 × 2)
Common factor is 1
Hence, the common factor = 1 [∵ 1 is a factor of every number]
(v) 6abc, 24ab2, 12a2b
= (2 × 3 × a × b × c), (2 × 2 × 2 × 3 × a × b × b) and (2 × 2 × 3 × a × a × b)
Common factors are 2 × 3 × a × b = 6ab
Hence, the common factor = 6ab
(vi) 16x3, -4x2, 32x
= (2 × 2 × 2 × 2 × x × x × x), -(2 × 2 × x × x), (2 × 2 × 2 × 2 × 2 × x)
Common factors are 2 × 2 × x = 4x
Hence, the common factor = 4x
(vii) 10pq, 20qr, 30rp
= (2 × 5 × p × q), (2 × 2 × 5 × q × r), (2 × 3 × 5 × r × p)
Common factors are 2 × 5 = 10
Hence, the common factor = 10
(viii) 3x2y2, 10x3y2, 6x2y2z
= (3 × x × x × y × y), (2 × 5 × x × x × x × y × y), (2 × 3 × x × x × y × y × z)
Common factors are x × x × y × y = x2y2
Hence, the common factor = x2y2.
Ex 14.1 Class 8 Maths Question 2.
Factorise the following expressions.
(i) 7x – 42
(ii) 6p – 12q
(iii) 7a2 + 14a
(iv) -16z + 20z3
(v) 20l2m + 30alm
(vi) 5x2y – 15xy2
(vii) 10a2 – 15b2 + 20c2
(viii) -4a2 + 4ab – 4ca
(ix) x2yz + xy2z + xyz2
(x) ax2y + bxy2 + cxyz
Solution:
(i) 7x – 42 = 7(x – 6)
(ii) 6p – 12q = 6(p – 2q)
(iii) 7a2 + 14a = 7a(a + 2)
(iv) -16z + 20z3 = 4z(-4 + 5z2)
(v) 20l2m + 30alm = 10lm(2l + 3a)
(vi) 5x2y – 15xy2 = 5xy(x – 3y)
(vii) 10a2 – 15b2 + 20c2 = 5(2a2 – 3b2 + 4c2)
(viii) -4a2 + 4ab – 4ca = 4a(-a + b – c)
(ix) x2yz + xy2z + xyz2 = xyz(x + y + z)
(x) ax2y + bxy2 + cxyz = xy(ax + by + cz)
Ex 14.1 Class 8 Maths Question 3.
Factorise:
(i) x2 + xy + 8x + 8y
(ii) 15xy – 6x + 5y – 2
(iii) ax + bx – ay – by
(iv) 15pq + 15 + 9q + 25p
(v) z – 7 + 7xy – xyz
Solution:
(i) x2 + xy + 8x + 8y
Grouping the terms, we have
x2 + xy + 8x + 8y
= x(x + y) + 8(x + y)
= (x + y)(x + 8)
Hence, the required factors = (x + y)(x + 8)
(ii) 15xy – 6x + 5y – 2
Grouping the terms, we have
(15xy – 6x) + (5y – 2)
= 3x(5y – 2) + (5y – 2)
= (5y – 2)(3x + 1)
(iii) ax + bx – ay – by
Grouping the terms, we have
= (ax – ay) + (bx – by)
= a(x – y) + b(x – y)
= (x – y)(a + b)
Hence, the required factors = (x – y)(a + b)
(iv) 15pq + 15 + 9q + 25p
Grouping the terms, we have
= (15pq + 25p) + (9q + 15)
= 5p(3q + 5) + 3(3q + 5)
= (3q + 5) (5p + 3)
Hence, the required factors = (3q + 5) (5p + 3)
(v) z – 7 + 7xy – xyz
Grouping the terms, we have
= (-xyz + 7xy) + (z – 7)
= -xy(z – 7) + 1 (z – 7)
= (-xy + 1) (z – 1)
Hence the required factor = -(1 – xy) (z – 7)


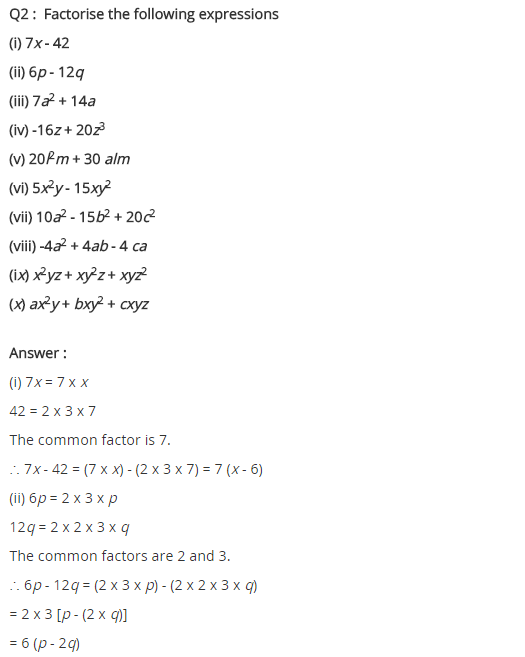



More CBSE Class 8 Study Material
- NCERT Solutions for Class 8 Maths
- NCERT Solutions for Class 8 Science
- NCERT Solutions for Class 8 Social Science
- NCERT Solutions for Class 8 English
- NCERT Solutions for Class 8 English Honeydew
- NCERT Solutions for Class 8 English It So Happened
- NCERT Solutions for Class 8 Hindi
- NCERT Solutions for Class 8 Sanskrit
- NCERT Solutions