NCERT Solutions For Class 6 Maths Practical Geometry Exercise 14.2
NCERT Solutions For Class 6 Maths Chapter 14 Practical Geometry Ex 14.2
Exercise 14.2
Ex 14.2 Class 6 Maths Question 1.
Draw a line segment of length 7.3 cm using ruler.
Solution:
Step I: Mark at point P.
Step II : Place the O mark of the ruler against the point P.
Step III : Mark a point Q at a distance of 7.3 cm from P.
Step IV : Join P and Q.
![]()
Thus \(\overline { PQ }\) is the line segment of length 7.3 cm.
Ex 14.2 Class 6 Maths Question 2.
Construct a line segment of length 5.6 cm using ruler and compass.
Solution:
Step I: Draw any line L of suitable lengths.
Step II : Place the needle of the compass on the zero mark of the ruler and open it upto 5.6 mark.
Step III : Place the needle at any point A at the line and draw an arc to cut l at B.
![]()
Thus, \(\overline { AB }\) is the required line segment of length 5.6 cm.
Ex 14.2 Class 6 Maths Question 3.
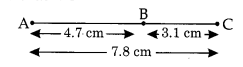
Construct \(\overline { AB }\) of length 7.8 cm. From this, cut off \(\overline { AC }\) of length 4.7 cm. Measure \(\overline { BC }\) .
Solution:
Given that \(\overline { AB }\) = 7.8 cm and \(\overline { AC }\) = 4.7 cm.
Step I : Place zero mark of the ruler at A.
Step II : Mark a point B at a distance of 7.8 cm from A.
Step III : Mark another point C at a distance of 4.7 cm from A such that AC = 4.7 cm.
Step IV : On measuring the length of BC, we find that \(\overline { BC }\) = 3.1 cm.
Ex 14.2 Class 6 Maths Question 4.
Given \(\overline { AB }\) of length 3.9 cm. Construct \(\overline { PQ }\) such that the length of \(\overline { PQ }\) is twice that of \(\overline { AB }\). Verify by measurement.
![]()
(Hint : Construct \(\overline { PX }\) such that the length of \(\overline { PX }\) = length of \(\overline { AB }\) then cut off \(\overline { XQ }\) such that \(\overline { XQ }\) also has the length of \(\overline { AB }\).
Solution:
Step I: Draw a line l of suitable length.
Step II: Draw \(\overline { AB }\) = 3.9 cm
Step III: From the line, construct \(\overline { PX }\) = \(\overline { AB }\) = 3.9 cm.
Step IV: Again construct \(\overline { XQ }\)= \(\overline { AB }\) =3.9 cm
Verification: \(\overline { PX }\) + \(\overline { XQ }\) = \(\overline { AB }\) + \(\overline { AB }\)
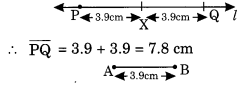
Thus twice of \(\overline { AB }\) is equal to \(\overline { PQ }\)
Ex 14.2 Class 6 Maths Question 5.
Given \(\overline { AB }\) of length 7.3 cm and \(\overline { CD }\) of length 3.4 cm, construct a line segment \(\overline { XY }\) such that the length of XY is equal to the difference between the length of \(\overline { AB }\) and \(\overline { CD }\) . Verify the measurement.
Solution:
Step I : Construct \(\overline { AB }\) = 7.3 cm and \(\overline { CD }\) = 3.4 cm.
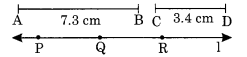
Step II: Take a point P on the given line l.
Step III: Construct \(\overline { PR }\) such that \(\overline { PR }\) = \(\overline { AB }\) = \(\overline { AB }\) = 7.3 cm.
Step IV:Construct \(\overline { RQ }\) = \(\overline { CD }\) = 3.4 cm such that PQ = \(\overline { AB }\) – \(\overline { CD }\) .
Verification : On measuring, we observe that \(\overline { PQ }\) = 3.9 cm = 7.3 cm 3.4 cm.
= \(\overline { AB }\) – \(\overline { CD }\)
Thus, \(\overline { PQ }\) = \(\overline { AB }\) – \(\overline { CD }\).




NCERT SolutionsMathsScienceSocialEnglishHindiSanskritRD Sharma