NCERT Solutions for Class 5 Maths Chapter 7 Can You See The Pattern?
NCERT Textbook Page 99
Pattern 1

1.

Ans.In pattern 1, we can see clearly that the rule is: one up, one down. Then this is repeated.

In pattern II, the rule is: it is once up, then takes a 1/4 turn every time. The rule is to repeat it with 1/4 clockwise turn.

In pattern III, the rule is : 1/4 turn anti-clockwise.

NCERT Textbook Pages 100-102
Practice Time
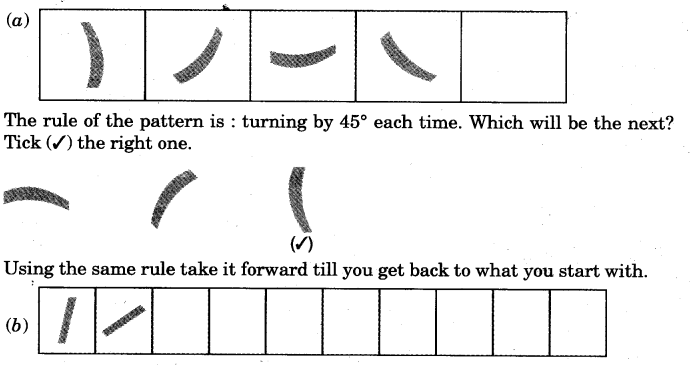
1.What should come next?
Ans. Answer figures are given in last two boxes.
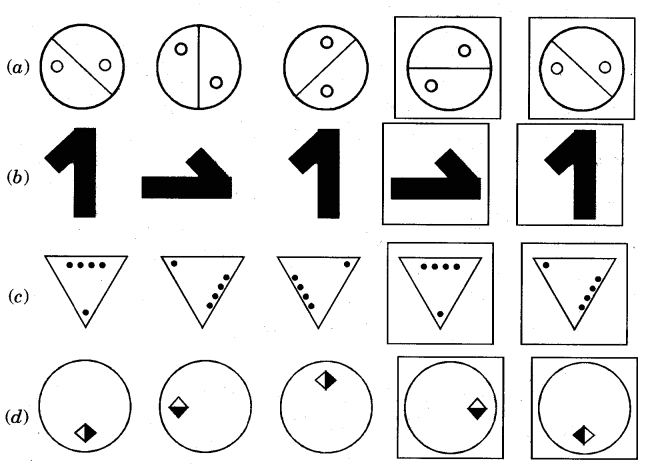
2.See this Pattern

Ans.
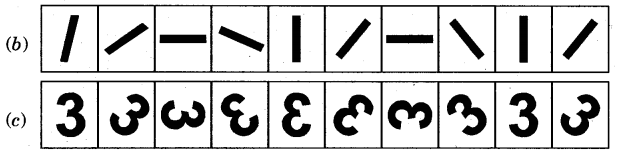
3.Some patterns are given below on the left side of the red line. For each pattern, write the rule. Then choose what comes next from the right side of the line and tick (right) it.
Ans.
NCERT Textbook Page 103
Look for a Pattern
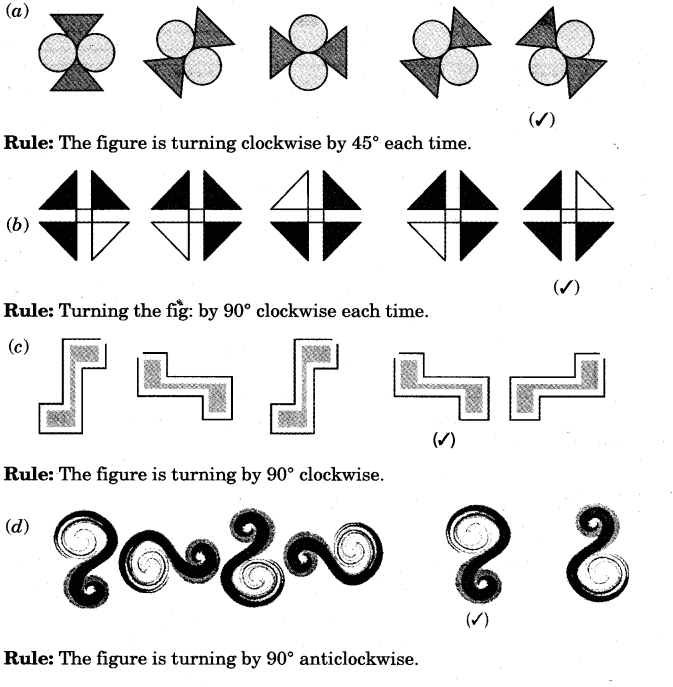
1.Mark that picture which is breaking the rule. Also correct it.
Ans. (a) In this pattern the sixth figure from the left is breaking the rule.
Correct figure is as follows:
(b)The sixth figure from left is breaking the rule.
(c)The second figure from left is breaking the rule. Correct figure is as follows:
(d)The fourth figure from left is breaking the rule. Correct figure is as follows:
Magic Squares
Do you remember magic triangles? Come now, let’s make some magic squares.
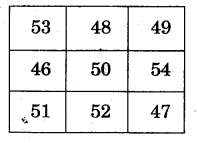
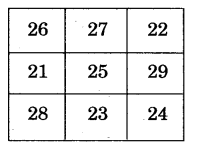
1.Fill this square using all the numbers from 46 to 54.
Rule: The total of each line is 150
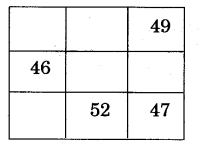
Ans. In the third row, we have
52 + 47 =99
And 150-99 =51
So, we can fill 51 in the first box of the third row.
Now, in the first column, we have 46 + 51 =97
And 150-97 =53
So, we can fill 53 in the first box of the first column.
In the first row, we have
53 + 49 = 102
And 150 – 102 = 48
So, we can fill 48 in the second box of the first row.
In the second column, We have
48 + 52 =100
And 150-100 =50
So, we can fill 50 in the second box of the second column. In the third row, we have
49 + 47 =96
And 150 – 96 = 54
So, we can fill 54 in the second box of the third column.
2.Fill this square using all the numbers from 21 to 29. Rule: The total of each side is 75.
Ans. In the first row:
The required number =75 – (26 + 22)
=75 – 48 = 27
In the first column:
The required number=75 – (26 + 28)
=75 – 54 = 21
In the second row:
The required number=75 – (21 + 25)
=75 = 75 – 46 = 29
In the third row:
The required number=75 – (28 + 24)
=75 – 52 = 23
Hence, the complete magic square is as follows:
NCERT Textbook Page 104
Magic Hexagons
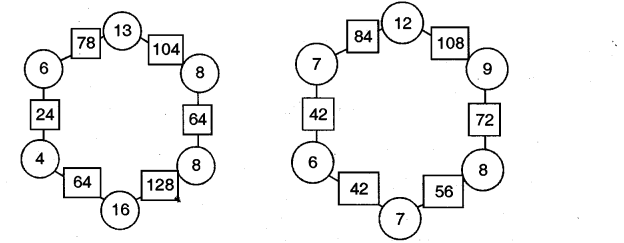
1.Leek at the patterns of numbers in hexagons. Each side has 2 circles and 1 box. You get the number in each box by multiplying the numbers in the circles next to it.
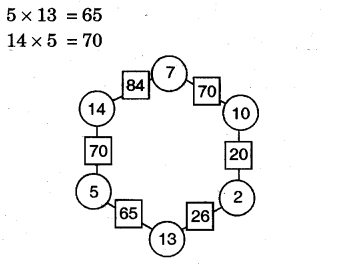
Look at the number 65 in the box.
Which are the circles next to it?
Can you see how tite rule works?
Use the same rule to fill the hexagons below:
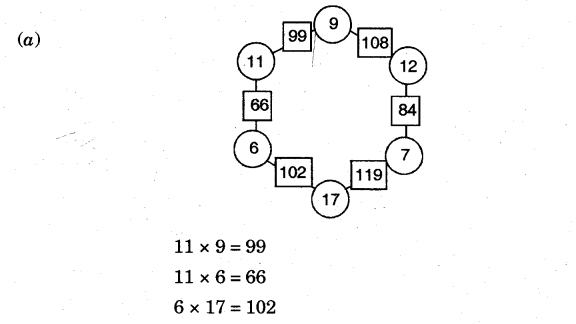
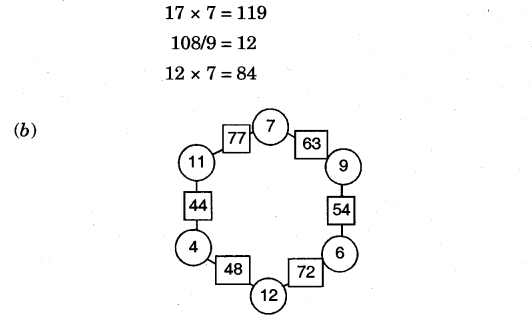
2.Now you also make your own magic hexagons.
Ans. Some of the magic hexagons are given below:
NCERT Textbook Page 105
Numbers and Numbers
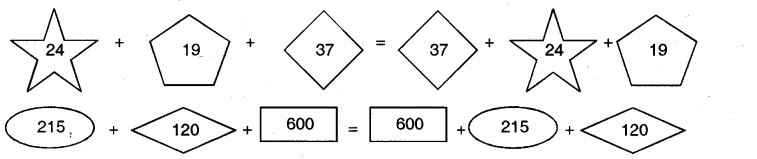
1.Are they equal?
Ans.Yes they are equal.
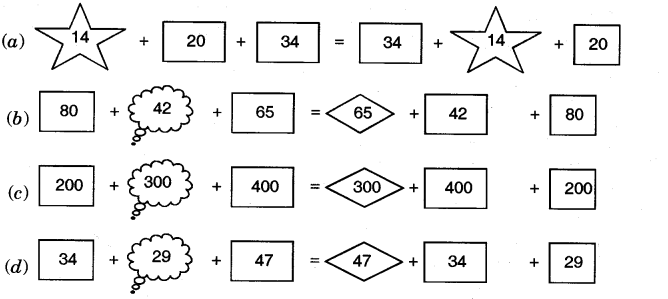
2.Fill in the blank spaces in the same way.
Ans.
3.Now look this
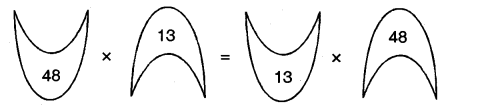
Ans.
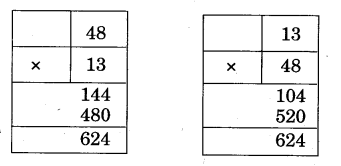
Left Right—Same to Same
1.Can you see something special about 121?
Ans. The number reads the same in backward and forward.
2.What, it’s just a number!
Ans. Oh, yes! It is 1, 2, 1 from right to left also.
Take a number, say : 43
Now turn it back to front : 34
Then add them together : 77
77 is one such special number. There are many such numbers. Take another number : 48
Now turn it back to front : 84
Then add them together : 132
3.Is this a special number? No! Why not?
Ans. Because it is not the same after reversing it.
OK, carry on with the number : 132
Again turn it back.to front : 231
Then add the two together : 363
Ah 1 363 is a special number.
Ans. Yes, it is a special number.
So we see that to get special numbers we sometime need more steps. Now you try and change these numbers into special numbers:
(а)28
Ans. 82
110 This is not a special number; so let us do more steps Oil
121 This is a special number
(b)132
Ans. 231
363 This is a special number
(c) 273
Ans. 372
645 This is not a special number; so let us do more steps 546
1191 This is not a special number; so let us do more steps 1911
3102 This is not a special number; so let us do more steps 2013
5115 This is a special number
4.Now let’s use words in special way.

Did you notice that it reads the same from both sides; right to left and left to right?
Now try and use words in a special way.
Ans. Some such examples are given below:
BACON NO CAB
BAR CANOE ON A CRAB
DENNIS SINNED
EVIL OLIVE
NCERT Solutions for Class 5 Maths Chapter 7 Page 107
Calendar Magic
Look at the calendar below:
Let us mark a 3 x 3 box (9 dates) on the calendar and see some magic
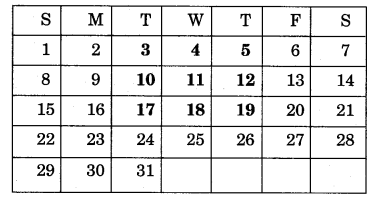
Take the smallest number:3
Add 8 to it: +8
= 11
Multiply by 9:x 9
Total: 99
99 is equal to the sum of all these numbers.
Now you choose any 3×3 box from a calendar and find the total in the same way. Play this game with your family.
Let us take 4
Add 8 to it +8
= 12
Multiply it by 9
= 9 x 12 = 108
This is equal to the sum of these 9 numbers.
To get the answer even faster multiply the middle number by 9, i.e. 12 x 9 = 108.
NCERT Solutions for Class 5 Maths Chapter 7 Page 108
Some More Number Patterns
1.Take any number. Now multiply it by 2, 3, 4————- at every step. Also add 3 to it at each step. Look at the difference in the answer. Is it the same at every step?
12 x 2 + 3 = 27
12 x 3 + 3 = 39
12 x 4 + 3 = 51
12 x 5 + 3 =63
12 x + 3 =—————-
———–x 7 + 3 =————
Ans.12 x 6 + 3 = 75
12 x 7 + 3 = 87
12 x 8 + 3 =99
12 x 9 + 3 =111 .
In every case the difference between consecutive numbers is 12
2.Now try doing it with some other number and also take a different number to add at each step.
Ans. Let us take another number to see the pattern;
15 x 2 + 5 =35
15 x 3 + 5 = 50
15 x 4 + 5 =65
15 x 5 + 5 =80
15 x 6 + 5 = 95
15 x 7 + 5 = 110
15 x 8 + 5 = 125
We can see the difference between two subsequent numbers is 15
3.Look at the numbers below. Look for the pattern. Can you take it forward?
(9-1) ÷8 =1
(98 – 2) ÷8 = 12
(987 – 3) ÷8 = 123
(9876 – 4) ÷8 = ………….
(98765-4) ÷8 = …………
(…………. -………….. ) ÷8 =………….
(…………….. -…………)÷8 = ……………
Ans.The above pattern is not correct. The correct pattern is as follows:
(9876 – 4) ÷8 = 1234
(98765-5)÷8 =12345
(987654 – 6) ÷8 =123456
(9876543 – 7) ÷8 =1234567
NCERT Solutions for Class 5 Maths Chapter 7 Page 109
Smart Adding
1.What if someone gives you to add ten numbers together?
Ans. Multiply 10/2 by (10 + 1) = 5 x 11 = 55
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 =55
11 + 12 + .. .. + .. .. + .. .. + .. .. + .. .. + .. .. + .. .. + 20 =155
21 + .. .. + .. .. + .. .. + .. .. + .. .. + .. ,. + .. .. + .. .. + 30 = ….
31 + .. .. + ., .. + .. .. + .. .. + .. .. + .. .. + .. .. + ., .. + 40 =….
41 + .. .. + ., .. + .. .. + .. .. + .. .. + .. .. + .. .. + .. .. + 50 = ….
51 + .. .. + ., .. + .. .. + .. .. + .. , . + . , .. + .. .. + .. .. + 60 =555
61 + .. .. + .. .. + .. .. + .. .. + .. .. + .. .. + .. .. + .. .. + 70 = ….
2.Did you notice some pattern in the answers?
Ans. Yes, I have noticed some pattern; sum of 1 to 10 is 55, sum of 11 to 20 is 155, sum of 21 to 30 is 255 and so on.
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 =55 11 + 12 + 13 + 14 + 15 + 16 + 17 + 18 + 19 + 20 = 155
21 + 22 + 23 + 24 + 25 + 26 + 27 + 28 + 29 + 30 = 255
31 + 32 + 33 + 34 + 35 + 36 + 37 + 38 + 39 + 40 = 355
41 + 42 + 43 + 44 + 45 + 46 + 47 + 48 + 49 + 50 = 455
51+ 52 + 53 + 54 + 55 + 56 + 57 + 58 + 59 + 60 = 555
61 + 62 + 63 + 64 + 65 + 66 + 67 + 68 + 69 + 70 = 655
Fun with Odd Numbers
Take the first two odd numbers. Now add them, see what you get.
Now, at every step, add the next odd number.
1 + 3 = 4 =2 x 2
1+3+5=9=3 x 3
1 + 3 + 5 + 7 = 16 =4 x 4
l+3 + 5 + 7 + 9 = … =… x …
1 + 3 + 5 + 7 + 9 + 11 = …=… x ….
1 + 3 + 5 + 7 + 9 + 11 + 13 = … = … x …
1.How far can you go on?
Ans. Complete patterns are as follows:
1+3 + 5 + 7 + 9 = 25=5 x 5
1 + 3 + 5 + 7 + 9 + 11 = 36 = 6 x 6
1 + 3 + 5 + 7 + 9 + 11 + 13 = 49 =7 x 7
This process can go on and on.
The sum of first ‘n’ odd numbers can be given by ‘n x n’
NCERT Solutions for Class 5 Maths Chapter 7 Page 110
Secret Numbers
Banno and Binod were playing a guessing game by writing clues about a secret number. Each tried to guess the other’s secret number from the clues.
1. Can you guess their secret numbers?
Ans.
- It is larger than half of 100.
- It is more than 6 tens and less than 7 tens.
- The tens digit is one more than the ones digit.
- Together the digits have a sum of 11.
2.What is my secret number?
Ans. Let us find this number.
- It is larger than half of 100 means > 50.
- It is more than 6 tens and less than 7 tens means the number is between 60 and 70.
- The tens digit is one more than the ones digit means ones digit is 6 – 1 = 5.
- Hence the number is 65.
- It also means that sum of the digits is 11.
3.It is smaller than half of 100.
It is more than 4 tens and less than 5 tens.
The tens digit is two more than the ones digit.
Together the digits have a sum of 6.
What is my secret number?
Ans. The number is less than 50 and more than 40. Hence the tens digit is 4 and ones digit is 6 – 4 = 2. The secret number is 42.
4.Write a set of clues for a secret number of your own. Then give it to a friend to guess your secret number.
Ans. A set of clues to find the secret number are as follows:
- It is larger than half of 100.
- It is more than 6 tens and less than 7 tens.
- The tens digit is two less than the ones digit.
- The sum of the digits is 14.
- Find the secret number.
- It is smaller than half of 100.
- It is more than 3 tens and less than 4 tens.
- The digit sum is 10.
- Find the secret number.
NCERT Solutions for Class 5 Maths Chapter 7 Page 111
Number Surprises
(a) Ask your friend—Write down your age. Add 5 to it. Multiply the sum by 2.
Subtract 10 from it. Next divide it by 2. What do you get?
Is your friend surprised?
Ans. Age = 9
Add 5 to it: 9 + 5 = 14
Multiply the sum by 2: 2 x 14 = 28
Subtract 10 from it: 28 – 10 = 18
Divide it by 2: 18÷2 = 9
The answer is same as my friend’s age. So, he must be surprised.
(b) Take a number = ….
Double it: …. x 2 = ….
Multiply by 5: …. x 5 = ….
Divide your answer by 10: …. ÷10 = …
Ans. Let us take the number 9
9 x 2 = 18
18 x 5 = 90
90 ÷10 = 9
Which is equal to the number taken.
(c)Take a number =…
Double it: … x 2 = …
Again double it: …. x 2 = ….
Add the number you took first to the answer Now again double it: …. x 2 = …
Divide by 10: …. ÷10 = …
Ans. Let us take the number 8
8 x 2 = 16
16 x 2 = 32
32 + 8 = 40
40 x 2 = 80
80÷10 = 8
Which is same as the number taken.
(d)Look at this pattern of numbers and take it forward
1 = 1 x 1
121= 11 x 11
12321 =111x 111
1234321 = ?
Ans. The pattern of numbers hints at following answer: 1234321=1111x 1111 Similarly, 123454321 = 11111 x 11111
2.Now make your own number surprises.
Ans. Some examples are as follows:
Take a number = …
Multiply by 4 : … x 4 = …
Add the number taken first: + … = ….
Divide by 5: ….÷5 = …
Let us take 11
11 x 4=44
44 + 11=55
55 ÷5 = 11
NCERT SolutionsMathsEVSEnglishHindiParyavarana Adhyayan