Get Free NCERT Solutions for Class 12 Maths Chapter 7 Integers Ex 7.10 PDF. Integration Class 12 Maths NCERT Solutions are extremely helpful while doing your homework. Exercise 7.10 Class 12 Maths NCERT Solutions were prepared by Experienced LearnCBSE.in Teachers. Detailed answers of all the questions in Chapter 7 Maths Class 12 Integrals Exercise 7.10 provided in NCERT Textbook.
Free download NCERT Solutions for Class 12 Maths Chapter 7 Exercise 7.10 Integrals PDF in Hindi Medium as well as in English Medium for CBSE, Uttarakhand, Bihar, MP Board, Gujarat Board, BIE, Intermediate and UP Board students, who are using NCERT Books based on updated CBSE Syllabus for the session 2019-20.
The topics and sub-topics included in the Integrals chapter are the following:
| Section Name | Topic Name |
| 7 | Integrals |
| 7.1 | Introduction |
| 7.2 | Integration as an Inverse Process of Differentiation |
| 7.3 | Methods of Integration |
| 7.4 | Integrals of some Particular Functions |
| 7.5 | Integration by Partial Fractions |
| 7.6 | Integration by Parts |
| 7.7 | Definite Integral |
| 7.8 | Fundamental Theorem of Calculus |
| 7.9 | Evaluation of Definite Integrals by Substitution |
| 7.10 | Some Properties of Definite Integrals |
- Integration Formulas
- Integrals Class 12 Ex 7.1
- Integrals Class 12 Ex 7.1 in Hindi Medium
- Integrals Class 12 Ex 7.2
- Integrals Class 12 Ex 7.2 in Hindi Medium
- Integrals Class 12 Ex 7.3
- Integrals Class 12 Ex 7.3 in Hindi Medium
- Integrals Class 12 Ex 7.4
- Integrals Class 12 Ex 7.4 in Hindi Medium
- Integrals Class 12 Ex 7.5
- Integrals Class 12 Ex 7.5 in Hindi Medium
- Integrals Class 12 Ex 7.6
- Integrals Class 12 Ex 7.6 in Hindi Medium
- Integrals Class 12 Ex 7.7
- Integrals Class 12 Ex 7.7 in Hindi Medium
- Integrals Class 12 Ex 7.8
- Integrals Class 12 Ex 7.8 in Hindi Medium
- Integrals Class 12 Ex 7.9
- Integrals Class 12 Ex 7.9 in Hindi Medium
- Integrals Class 12 Ex 7.10
- Integrals Class 12 Ex 7.10 in Hindi Medium
- Integrals Class 12 Ex 7.11
- Integrals Class 12 Ex 7.11 in Hindi Medium
- Integrals Class 12 Miscellaneous Exercise
- RD Sharma Class 12 Integrals
- NCERT Exemplar Class 12 Maths Integrals
- Integrals Class 12 Notes Maths Chapter 7
- Important Questions Class 12 Maths Integrals
- JEE Main Mathematics Definite and Indefinite Integrals
NCERT Solutions for Class 12 Maths Chapter 7 Integers Ex 7.10
NCERT Solutions for Class 12 Maths Chapter 7 Integers Ex 7.10 are part of NCERT Solutions for Class 12 Maths. Here we have given Class 12 Maths NCERT Solutions Integrals Ex 7.10
Question 1:
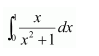
Solution:
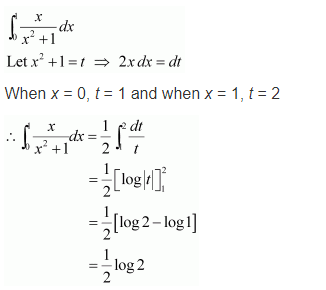
Question 2:

Solution:

Question 3:
![]()
Solution:

Question 4:
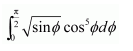
Solution:

Question 5:

Solution:


Question 6:

Solution:

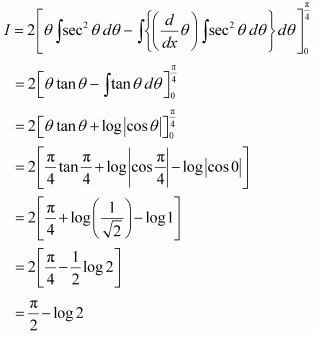
Question 7:
![]()
Solution:

Question 8:
![]()
Solution:

Question 9:

Solution:

Question 10:
![]()
Solution:

Question 11:
![]()
Solution:
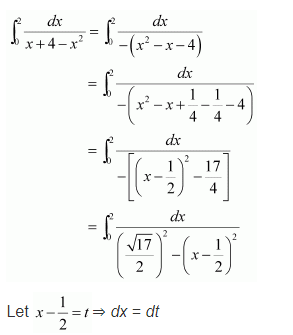



Question 12:
![]()
Solution:



Question 13:
![]()
Solution:

Question 14:
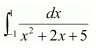
Solution:

Question 15:
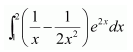
Solution:
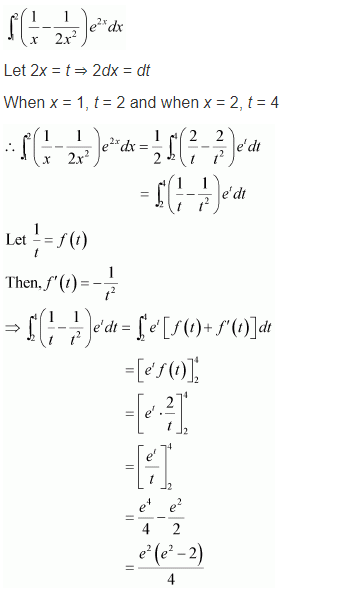
Question 16:
![]()
Solution:
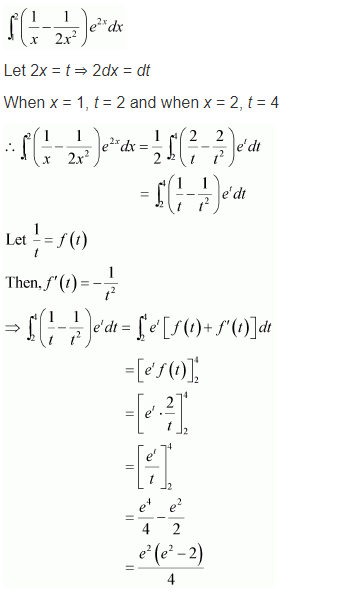
Question 17:

Solution:


Question 18:

Solution:


Question 19:
![]()

Solution:

Question 20:
![]()

Solution:

NCERT Solutions for Class 12 Maths Chapter 7 Integers Ex 7.10 in Hindi Medium
प्रश्न 1 से 8 तक के प्रश्नों में समाकलनों का मान प्रतिस्थापन का उपयोग करते हुए ज्ञात कीजिए।
प्रश्न 1.
\(\int_{0}^{1} \frac{x}{x^{2}+1} d x\)
हल-
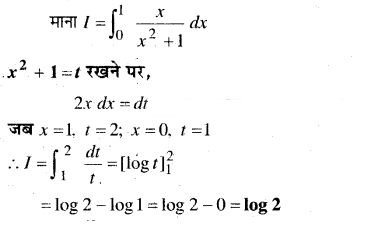
प्रश्न 2.
\(\int_{0}^{\pi / 2} \sqrt{\sin \phi} \cos ^{5} \phi d \phi\)
हल-

प्रश्न 3.
\(\int_{0}^{1} \sin ^{-1}\left(\frac{2 x}{1+x^{2}}\right) d x\)
हल-
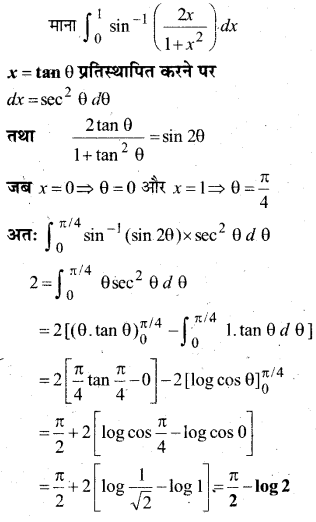
प्रश्न 4.
\(\int_{0}^{2} x \sqrt{x+2} d x\)
हल-

प्रश्न 5.
\(\int_{0}^{\pi / 2} \frac{\sin x}{1+\cos ^{2} x} d x\)
हल-

प्रश्न 6.
\(\int_{0}^{2} \frac{d x}{x+4-x^{2}}\)
हल-
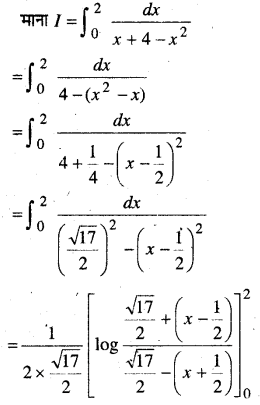
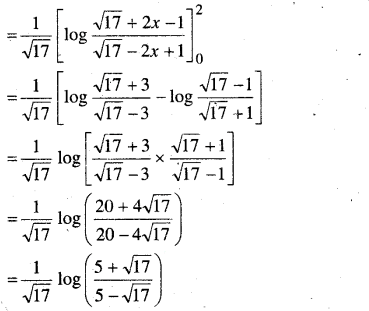
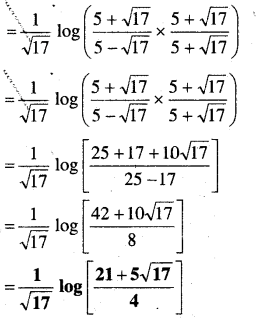
प्रश्न 7.
\(\int_{-1}^{1} \frac{d x}{x^{2}+2 x+5}\)
हल-
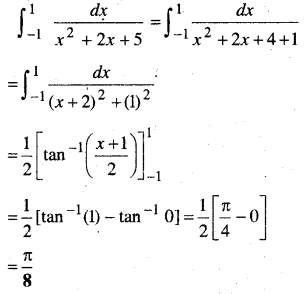
प्रश्न 8.
\(\int_{1}^{2}\left(\frac{1}{x}-\frac{1}{2 x^{2}}\right) e^{2 x} d x\)
हल-
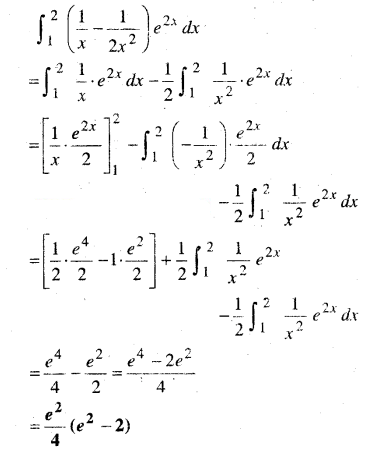
प्रश्न 9 एवं 10 में सही उत्तर का चयन कीजिए
प्रश्न 9.
समाकलन \(\int_{1 / 3}^{1} \frac{\left(x-x^{3}\right)^{1 / 3}}{x^{4}} d x\) का मान है-
(A) 6
(B) 0
(C) 3
(D) 4
हल-
x = sin θ रखने पर
dx = cos θ dθ
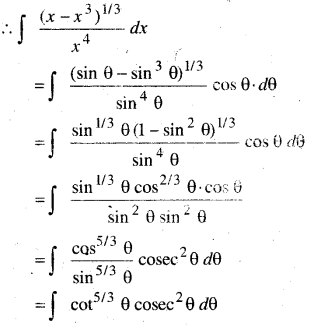
पुनः cot θ = t प्रतिस्थापित करने पर
-cosec2θ dθ = dt
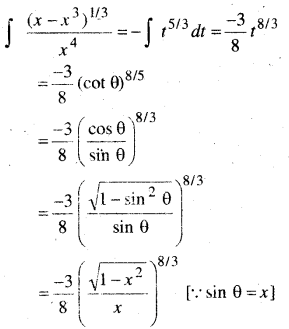
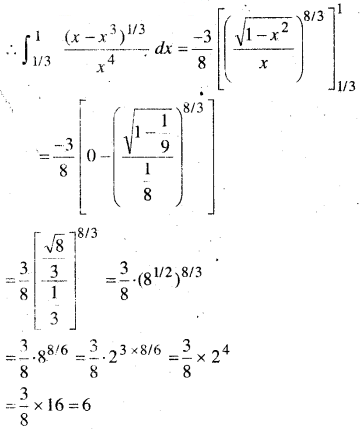
अतः विकल्प (A) सही है।
प्रश्न 10.
यदि f(x) = \(\int_{0}^{x} t \sin t d t\) है, तब f'(x) है-
(A) cos x + x sin x
(B) x sin x
(C) x cos x
(D) sin x + x cos x
हल-
f(x) = \(\int_{0}^{x} t \sin t d t\)
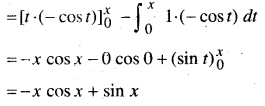
अतः f'(x) = -[cos x – x sin x] + cos x
= – cos x + x sin x + cos x
= x sin x
अतः विकल्प (B) सही है।
Class 12 Maths NCERT Solutions
- Chapter 1 Relations and Functions
- Chapter 2 Inverse Trigonometric Functions
- Chapter 3 Matrices
- Chapter 4 Determinants
- Chapter 5 Continuity and Differentiability
- Chapter 6 Application of Derivatives
- Chapter 7 Integrals Ex 7.1
- Chapter 8 Application of Integrals
- Chapter 9 Differential Equations
- Chapter 10 Vector Algebra
- Chapter 11 Three Dimensional Geometry
- Chapter 12 Linear Programming
- Chapter 13 Probability Ex 13.1