NCERT Solutions for Class 11 Maths Chapter 2 Miscellaneous Exercise

Get Free NCERT Solutions for Class 11 Maths Chapter 2 Relations and Functions Miscellaneous Exercise PDF in Hindi and English Medium. Relations and Functions Class 11 Maths NCERT Solutions are extremely helpful while doing your homework. Relations and Functions Miscellaneous Exercise Class 11 Maths NCERT Solutions were prepared by Experienced LearnCBSE.in Teachers. Detailed answers of all the questions in Chapter 2 Class 11 Relations and Functions Miscellaneous Exercise provided in NCERT Textbook.

• Relations and Functions Class 11 Ex 2.1
• Relations and Functions Class 11 Ex 2.2
• Relations and Functions Class 11 Ex 2.3
• Relations and Functions Class 11 Miscellaneous Exercise
• संबंध एवं फलन प्रश्नावली 2.1 का हल हिंदी में
• संबंध एवं फलन प्रश्नावली 2.2 का हल हिंदी में
• संबंध एवं फलन प्रश्नावली 2.3 का हल हिंदी में
• संबंध एवं फलन विविध प्रश्नावली का हल हिंदी में
• NCERT Exemplar Class 11 Maths Chapter 2 Relations and Functions
• Relations and Functions Class 11 Notes
• Relations and Functions Formulas
• RD Sharma Class 11 Solutions Chapter 2 Relations

Free download NCERT Solutions for Class 11 Maths Chapter 2 Relations and Functions Miscellaneous Exercise PDF in Hindi Medium as well as in English Medium for CBSE, Uttarakhand, Bihar, MP Board, Gujarat Board, BIE, Intermediate and UP Board students, who are using NCERT Books based on updated CBSE Syllabus for the session 2019-20.

NCERT Solutions for Class 11 Maths Chapter 2 Miscellaneous Exercise

Question-1
The relation f is defined by f (x) =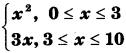
The relation g is defined by g(x) =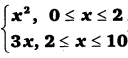
Show that f is a function and g is not a function.
Ans.
The relation f is defined as f (x) =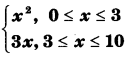
0 ≤ x < 3, f(x) = x²
3 ≤ x ≤ 10, f(x) = 3x
Also, at x = 3, f(x) = 3² = 9 or f(x) = 3 × 3 = 9
i.e., at x = 3, f(x) = 9
Therefore, for 0 ≤ x ≤ 10, the images of f(x) are unique.
Thus, the given relation is a function.
The relation g is defined as g (x) =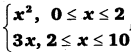
It can be observed that for x = 2, g(x) = 2² = 4 and g(x) = 3 × 2 = 6
Hence, element 2 of the domain of the relation g corresponds to two different images te., 4 and 6. Hence, this relation is not a function.

Question-2
If f(x) = x², find \(\frac{f(1.1)-f(1)}{(1.1-1)}\)
Ans.
f(x) = x²
∴ \(\frac{f(1.1)-f(1)}{(1.1-1)}\) = \(\frac{(1.1)^{2}-(1)^{2}}{(1.1-1)}\) = \(\frac{1.21-1}{0.1}\) = \(\frac{0.21}{0.1}\) = 2.1

Question-3
Find the domain of the function f(x) = \(\frac{x^{2}+2 x+1}{x^{2}-8 x+12}\)
Ans.
The given function is f(x) = \(\frac{x^{2}+2 x+1}{x^{2}-8 x+12}\)
f(x) = \(\frac{x^{2}+2 x+1}{x^{2}-8 x+12}\) = \(\frac{x^{2}+2 x+1}{(x-6)(x-2)}\)
It can be seen that function f is defined for all real numbers except at x = 6 and x = 2.
Hence, the domain off is R – {2, 6}.

Question-4
Find the domain and the range of the real function f defined by f(x) =
Answer.
Ans.
The given real function is f (x) = .
It can be seen that  is defined for (x – 1) ≥ 0.
i.e., f(x) =  is defined for x ≥ 1.
Therefore, the domain off is the set of all real numbers greater than or equal to 1 i.e., the domain of f = [1, ∞).
As x ≥ 1
⇒ (x – 1) ≥ 0
⇒  ≥ 0
Therefore, the range off is the set of all real numbers greater than or equal to 0 i.e., the range of f = [0, ∞).

Question-5
Find the domnin and the range of the real function f defined by f(x) = |x – 1|.

Ans.

The given real function isf (x) = |x – 1|.
It is clear that |x – 1| is defined for all real numbers.
∴ Domain of f = R
Also, for x ∈ R, |x – 1| assumes all real numbers.
Hence, the range of f is the set of all non-negative real numbers.

Question-6

Let f = \(\left\{\left(X, \frac{x^{2}}{1+x^{2}}\right)\right\}\) : x ∈ R be a function from R into R. Determine the range of f.

Ans.

f = \(\left\{\left(X, \frac{x^{2}}{1+x^{2}}\right)\right\}\) : x ∈ R

= {(0, 0), (±0.5, \(\frac{1}{5}\)), (±1, \(\frac{1}{2}\)), (±1.5, \(\frac{9}{13}\)), (±2, \(\frac{4}{5}\)), (3, \(\frac{9}{10}\)), (4, \(\frac{16}{17}\))}

The range of f is the set of all second elements. It can be observed that all these elements are greater than or equal to 0 but less than 1, [∵ Denominator is greater than numerator]
Thus, range of f = [0,1).

Question-7

Let f, g : R → R be defined, respectively by f(x) = x + 1, g(x) = 2x – 3. Find f + g, f – g and \(\frac{f}{g}\).

Ans.

f, g : R → R is defined as f(x) = x + 1, g(x) = 2x – 3
(i) (f + g) (x) = f(x) + g(x)
= (x + 1) + (2x – 3) = 3x – 2
∴ (f + g) (x) = 3x – 2

(ii) (f – g) (x) = f(x) – g(x)
= (x + 1) – (2x – 3)
= x + 1 – 2x + 3 = – x + 4
∴ (f – g) (x) = – x + 4

(iii) \(\frac{f}{g}\) (x) = \(\frac{f(x)}{g(x)}\), g(x) ≠ 0, x ∈ R.

∴ (\(\frac{f}{g}\))(x) = \(\frac{x+1}{2 x-3}\), 2x – 3 ≠ 0 or 2x ≠ 3

∴ (\(\frac{f}{g}\))(x) = \(\frac{x+1}{2 x-3}\), x ≠ \(\frac{3}{2}\).

Question-8
Let f ={(1, 1), (2, 3), (0, – 1), (- 1, – 3)} be a function from Z to Z defined by f(x) = ax + b, for some integers a, b. Determine a, b.
Ans.
f = {(1, 1), (2, 3), (0, – 1), (- 1, – 3)}
f(x) = ax + b
(1, 1) ∈ f
⇒ f (1) = 1
⇒ a × 1 + b = 1
⇒ a + b = 1
(0, – 1) ∈ f
⇒ f (0) = – 1
⇒ a × 0 + b = – 1
⇒ b = – 1
On substituting b= – 1 in a + b = 1, we obtain a + (- 1) = 1
⇒ a = 1 + 1 = 2.
Thus, the respective values of a and b are 2 and – 1.

Question-9

Let R be a relation from N to N defined by R = {(a, b) : a, b ∈ N and a = b²}. Are the following true?
(i) (a, a) ∈ R, for all a ∈ N
(ii) (a, b) ∈ R, implies (b, a) ∈ R
(iii) (a, b) ∈ R, (b, c) ∈ R implies (a, c) ∈ R.
Justify your answer in each case.

Ans.

R = {(a, b) : a, b ∈ N and a = b²}
(i) It can be seen that 2 ∈ N; however, 2 ≠ 2² = 4.
Therefore, the statement “(a, a) ∈ R, for all a ∈ N” is not true.

(ii) It can be seen that (9, 3) ∈ N because 9, 3 ∈ N and 9 = 3².
Now, 3 ≠ 9² = 81; therefore, (3, 9) ∈ N
Therefore, the statement “(a, b) ∈ R, implies (b, a) ∈ R is not true.

(iii) It can be seen that (16, 4) ∈ R, (4, 2) ∈ R because 16, 4, 2 e∈ N and 16 = 4² and 4 = 2².
Now, 16 ≠ 2² = 4; therefore, (16, 2) ∈ N
Therefore, the statement “(a, b) ∈ R, (b, c) ∈ R implies (a, c) ∈ R” is not true.

Question-10

Let A = {1, 2, 3, 4}, B = {1, 5, 9, 11, 15, 16} and f = {(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}. Are the following true?
(i) f is a relation from A to B
(ii) f is a function from A to B.
Justify your answer in each case.

Ans.

A = {1, 2, 3, 4} and B = {1, 5, 9,11, 15, 16}
∴ A × B = {(1, 1), (1, 5), (1, 9), (1, 11), (1, 15), (1, 16), (2, 1), (2, 5), (2, 9), (2, 11), (2, 15), (2,16), (3, 1), (3, 5), (3, 9),(3, 11),
(3, 15), (3, 16), (4, 1), (4, 5), (4, 9), (4, 11), (4, 15), (4, 16)}
It is given that f = {( 1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}.

(i) A relation from a non-empty set A to a non-empty set B is a subset of the Cartesian product A × B.
It is observed that f is a subset of A × B.
Thus, f is a relation from A to B.
(ii) Since the same first element i.e., 2 corresponds to two different images
i.e., 9 and 11, relation f is not a function.

Question-11
Let f be the subset of Z × Z defined by f = {(ab, a + b) : a,b ∈ Z}. Is f a function from Z to Z ? Justify your answer.
Ans.
The relation f is defined as f = {(ab, a + b) : a, b ∈ Z}
We know that a relation f from a set A to a set B is said to be a function if every element of set A has unique images in set B.
Since 2, 6, – 2, – 6 ∈ Z, (2 × 6, 2 + 6), (- 2 × – 6, – 2 + (- 6)) ∈ f.
i.e., (12, 8), (12, – 8)
It can be seen that the same first element i.e., 12 corresponds to two different images i.e., 8 and – 8.
Thus, relation f is not a function.

Question-12

Let A = {9, 10, 11, 12, 13} and let f: A→ N be defined by f(n) = the highest prime factor of n. Find the range of f.

Ans.
A = {9, 10,11, 12, 13}
f : A → N is defined as f(n) = The highest prime factor of n
Prime factor of 9 = 3;
Prime factors of 10 = 2, 5;
Prime factor of 11 = 11;
Prime factors of 12 = 2, 3;
Prime factor of 13 = 13
f(9) = The highest prime factor of 9 = 3
f(10) = The highest prime factor of 10 = 5 .
f(11) = The highest prime factor of 11 = 11
f(12) = The highest prime factor of 12 = 3
f(13) = The highest prime factor of 13 = 13
The range of f is the set of all f(n), where n ∈ A.
∴ Range of f = {3, 5, 11, 13}.

NCERT Solutions for Class 11 Maths Chapter 2 Relations and Functions Miscellaneous Exercise

अध्याय 2 पर विविध प्रश्नावली

 

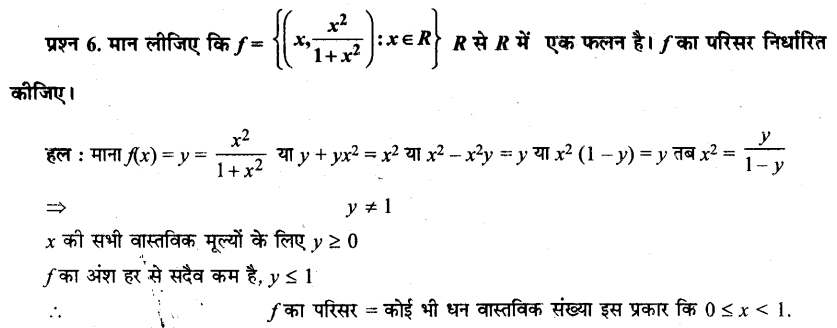
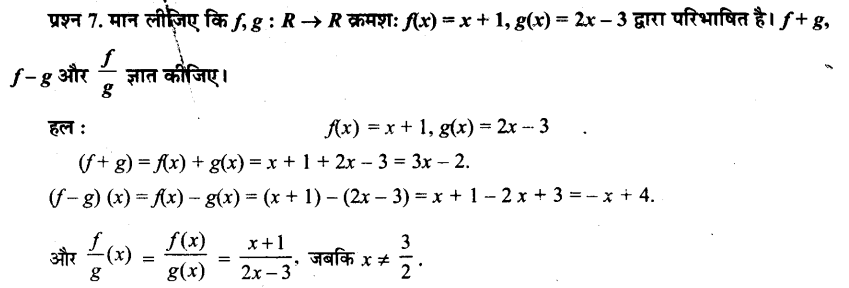
प्रश्न 8.
मान लीजिए कि f = {(1, 1), (2, 3), (0, -1), (-1, -3)} Z से Z में, f(x) = ax + b, द्वारा परिभाषित एक फलन है, जहाँ a, b कोई पूर्णाक हैं। a, b को निर्धारित कीजिए।
हल:
दिया है :
f = {(1, 1), (2, 3), (0, – 1), (-1, – 3)}
और f(x) = ax + b …..(A)
जब x = 1; y = 1, हो तब a + b = 1 …..(i)
और जबे x = 2, y = 3, 2a + b = 3 …..(ii)
समीकरण (i) और (ii) से,
a = 2, b = -1
a तथा b के इन मानों को समीकरण (A) में रखने पर,
f(x) = 2x – 1
जब x = 0, f(x) = -1
और जब x = -1, f(x) = -3
अतः f(x) = 2x – 1 तथा a = 2, b = -1.

प्रश्न 9.
R = {(a, b) : a, b ∈ N तथा a = b2} द्वारा परिभाषित N से N में, एक संबंध R है। क्या निम्नलिखित कथन सत्य है।
(i) {a, a} ∈ R सभी a ∈ N
(ii) (a, b) ∈ R का तात्पर्य है कि (b, a) ∈ R
(iii) (a, b) ∈ R, (b, c) ∈ R का तात्पर्य है कि (a, c) ∈ R? प्रत्येक दशा में अपने उत्तर का औचित्य भी बताइए।
हल:
(i) a = a यह सत्य है जब a = 0, 0 ∉ N,
अत: यह एक संबंध नहीं है।
(ii) a = b2, और b = a2, यह a, b ∈ N, a, b के सभी मूल्यों के लिए सत्य नहीं है। अत: यह एक संबंध नहीं है।
(iii) जब a = b2, b = c2 तब a ≠ c2
यह संबंध नहीं है।

प्रश्न 10.
मान लीजिए A = {1, 2, 3, 4}, B = {1, 5, 9, 11, 15, 16} और f = {(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}, क्या निम्नलिखित कथन सत्य है ?
(i) f, Aसे B में एक संबंध है।
(ii) f, A से B में एक फलन है। प्रत्येक दशा में अपने उत्तर का औचित्य बताइए।
हल:
(i) दिया है: A = {1, 2, 3, 4} तथा B = {1, 5, 9, 11, 15, 16}
A x B = {(1, 1), (1, 5), (1, 9), (1,11), (1, 15), (1, 16), (2, 1), (2, 5), (2, 9), (2, 11), (2, 15), (2, 16), (3, 1), (3, 5), (3, 9), (3, 11), (3, 15), (3,16), (4, 1), (4, 5), (4,9), (4, 11), (4, 15), (4, 16)}
अवयव, A x B का उपसमुच्चय है।
अतः यह एक संबंध है।
(ii) f में (2, 9) और (2, 11) अवयव प्रथम घटक दोनों युग्मों में 2 है।
यह फलन नहीं है।

प्रश्न 11.
मान लीजिए कि f, f = {(ab, a + b); a, b ∈ Z} द्वारा परिभाषित Z x Z का एक उपसमुच्चय है। क्या f, Z से Z में एक फलन है ? अपने उत्तर का औचित्य भी स्पष्ट कीजिए।
हल:
मान लीजिए a = 0, b = 1 हो, तब
ab = 0 और a + b = 0 + 1 = 1
पुनः माना a = 0, b = 2 हो, तब
ab = 0, a + b = 2.
अवयव 0 के दो प्रतिबिंब 1 और 2 हैं।
अत: f एक फलन नहीं है।

प्रश्न 12.
मान लीजिए कि A= {9, 10, 11, 12, 13} तथा f : A → N, f(n) = n का महत्तम अभाज्य गुणक द्वारा परिभाषित है।/का परिसर ज्ञात करो।
हल:
यदि n = 9 = 3 x 3 तो 3 इन गुणनखंडों में सबसे बड़ी अभाज्य संख्या है।
n= 10 = 2 x 5 तो 5 इन गुणनखंडों में सबसे बड़ी अभाज्य संख्या है।
n = 11 = 1 x 11 तो 11 इन गुणनखंडों में सबसे बड़ी अभाज्य संख्या है।
n = 12 = 22 x 3 तो 3 इन गुणनखंडों में सबसे बड़ी अभाज्य संख्या है।
n = 13 = 1 x 13 तो 13 इन गुणनखंडों में सबसे बड़ी अभाज्य संख्या है।
अतः f का परिसर = {3, 5, 11, 13}.