NCERT Exemplar Class 11 Physics Chapter 3 Motion in a Plane are part of NCERT Exemplar Class 11 Physics. Here we have given NCERT Exemplar Class 11 Physics Chapter 3 Motion in a Plane.
NCERT Exemplar Problems Class 11 Physics Chapter 3 Motion in a Plane
Multiple Choice Questions
Single Correct Answer Type
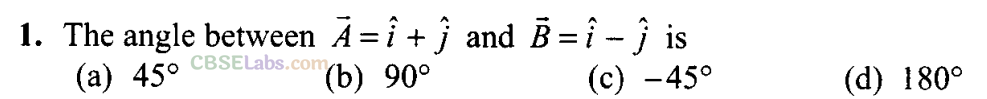
Sol: (b)
Key concept: Scalar Product of Two Vectors:
(1) Definition : The scalar product (or dot product) of two vectors is defined as the product of the magnitude of two vectors with cosine of angle between them.

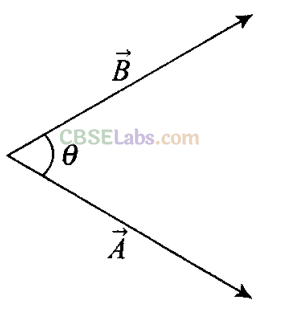


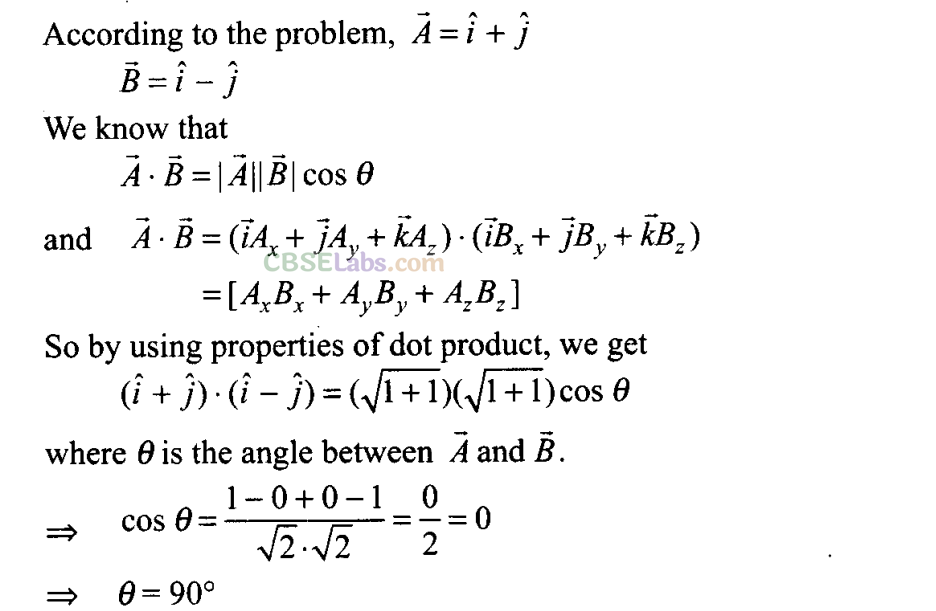
Q2. Which one of the following statements is true?
(a) A scalar quantity is the one that is conserved in a process.
(b) A scalar quantity is the one that can never take negative values.
(c) A scalar quantity is the one that does not vary from one point to another in space.
(d) A scalar quantity has the same value for observers with different orientation of the axes.
Sol: (d) A scalar quantity is independent of direction hence has the same value for observers with different orientations of the axes.
For example, a car is traveling along +x axis, it travels 10 m. If the same car is moving with the same speed for the same time interval along -x axis, then the distance meter of car shows the same travelled distance. The path length is same in both the cases.
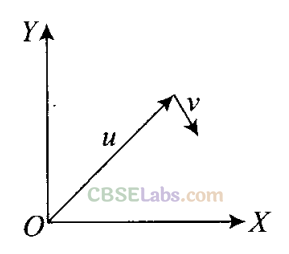
Q3. Figure shows the orientation of two vectors u and v in the TY-plane.
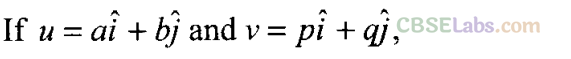
which of the following is correct?
(a) a and p are positive while b and q are negative
(b) a, p and b are positive while q is negative
(c) a, q and b are positive while p is negative
(d) a, b, p and q are all positive


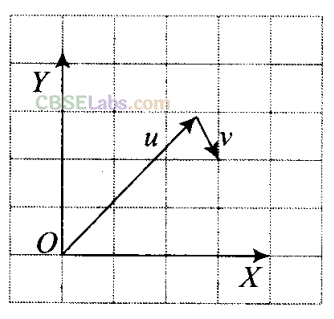
Here it is worthy to note once a vector is resolved into its components, the components themselves can be used to specify the vector as:

In such type of problems we have to resolve the rectangular components according to the diagram.

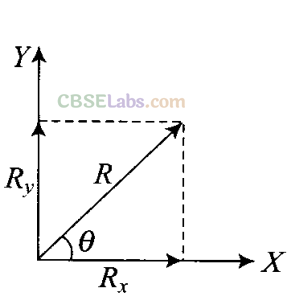
Q4. The component of a vector r along X-axis will have maximum value if
(a) r is along positive Y-axis
(b) r is along positive X-axis
(c) r makes an angle of 45° with the X-axis
(d) r is along negative Y-axis

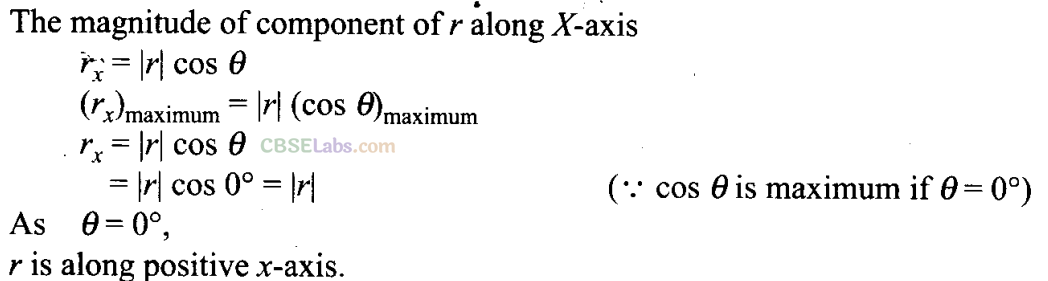
Q5. The horizontal range of a projectile fired at an angle of 15° is 50 m. If it is fired with the same speed at an angle of 45°, its range will be
(a) 60 m (b) 71m (c) 100 m (d) 141m

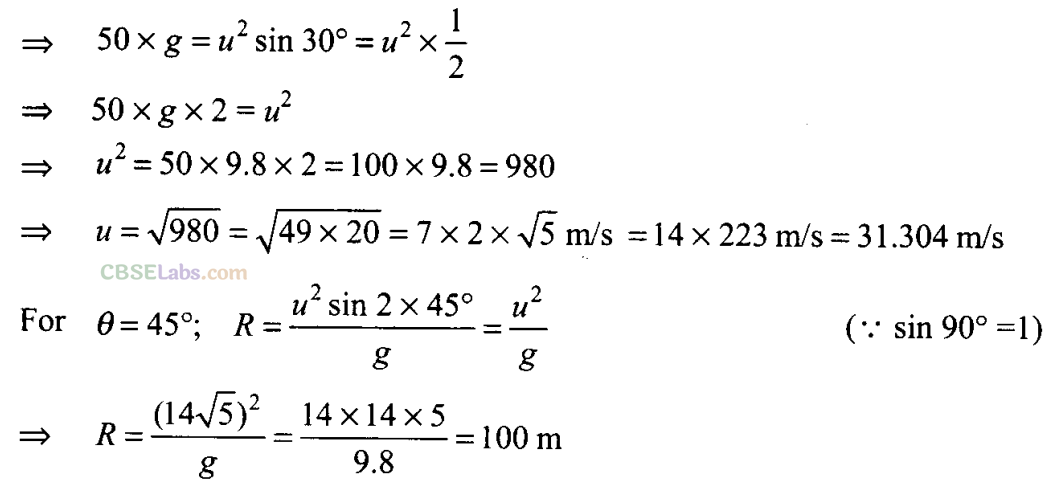
Q6. Consider the quantities pressure, power, energy, impulse, gravitational potential, electrical charge, temperature, area. Out of these, the only vector quantities are
(a) Impulse, pressure and area
(b) Impulse and area
(c) Area and gravitational potential
(d) Impulse and pressure
Sol: (b) We know that impulse J = F. ∆t = ∆p, where F is force, At is time duration and Ap is change in momentum. As ∆p is a vector quantity, hence impulse is also a vector quantity. Sometimes area can also be treated as vector direction of area vector is perpendicular to its plane.
Q7. In a two dimensional motion, instantaneous speed ==vo== is a positive constant. Then, which of the following are necessarily true?
(a) The average velocity is not zero at any time
(b) Average acceleration must always vanish
(c) Displacements in equal time intervals are equal
(d) Equal path lengths are traversed in equal intervals
Sol :(d) Speed (Instantaneous Speed): The magnitude of the velocity at any instant of time is known as Instantaneous Speed or simply speed at that instant of time. It is denoted by v.
Quantitatively: Speed = distance/ time
Mathematically, it is the time rate at which distance is being travelled by the particle.
• Speed is a scalar quantity. It can never be negative (as shown by speedometer of our vehicle).
• Instantaneous speed is the speed of a particle at a particular instant of time.
Hence, Total distance travelled = Path length = (speed) x time taken Important point: We should be very carefttl with the fact that speed is related with total distance covered not with displacement.
Q8. In a two-dimensional motion, instantaneous speed v0 is a positive constant. Then, which of the following are necessarily true?
‘(a) The acceleration of the particle is zero.
(b) The acceleration of the particle is bounded.
(c) The acceleration of the particle is necessarily in the plane of motion.
(d) The particle must be undergoing a uniform circular motion.
Sol. (c) This motion is two dimensional and given that instantaneous speed v0 is positive constant. Acceleration is defined as the rate of change of velocity (instantaneous speed), hence it will also be in the plane of motion.
Sol : (c) These types of problems can be solved by hit and trial method by picking up options one by one
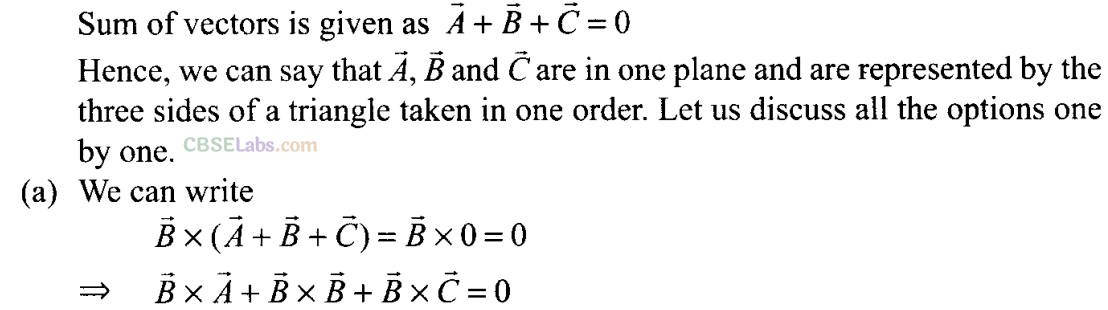
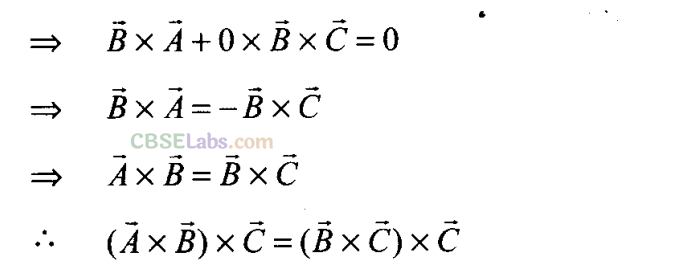

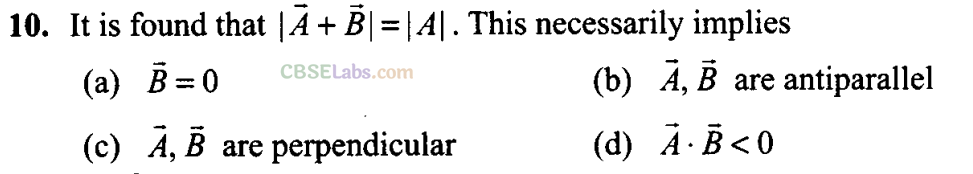
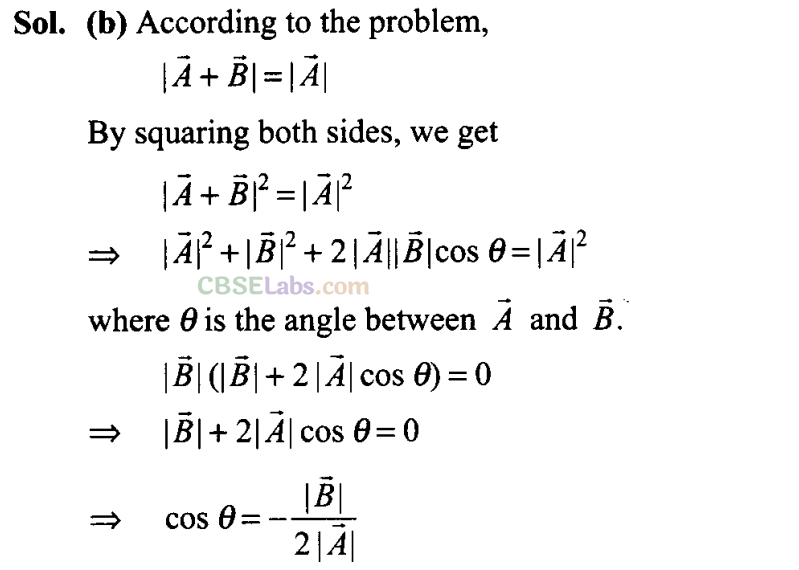

More Than One Correct Answer type
Q11. Two particles are projected in air with speed v0 at angles θ1 and θ 2 (both acute) to the horizontal, respectively. If the height reached by the first particle is greater than that of the second, then tick the right choices.
(a) Angle of projection: θ1 > θ2
(b) Time of flight: T1 > T2
(c) Horizontal range: Rx> R2
(d) Total energy: U1> U2

Q12. A particle slides down a frictionless parabolic (y = x2) track (A – B – C)
starting from rest at point A (figure). Point B is at the vertex of parabola and point C is at a height less than that of point A. After C, the particle moves freely in air as a projectile. If the particle reaches highest point at P, then
(a) KE at P = KE at B
(b) height at P = height at A
(c) total energy at P = total energy at A
(d) time of travel from AtoB
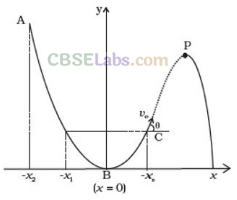
Solution : (c)
Key concept: In such type of problems, we have to observe the nature of track that if there is a friction or not, as friction is not present in this track, total energy of the particle will remain constant throughout the journey.
According to the problem, the path traversed by the particle on a frictionless track is parabolic, is given by the equation y = x2, thus total energy (KE + PE) will be same throughout the journey.
Hence, total energy at A = total energy at P
At B the particle is having only KE but at P some KE is converted to PE.
So, (KE)B > (KE)P
Total energy at A = PE = Total energy at B = KE = Total energy at P = PE + KE
The potential energy at A is converted to KE and PE at P, hence (PE)P < (PE)A
Hence, (Height) P < (Height) A
As, Height of P < Height of A
Hence, path length AB > path length BP
Hence, time of travel from A to B ≠ Time of travel from B to P.

Q14. For a particle performing uniform circular motion, choose the correct
statement(s) from the following.
(a) Magnitude of particle velocity (speed) remains constant.
(b) Particle velocity remains directed perpendicular to radius vector.
(c) Direction of acceleration keeps changing as particle moves.
(d) Angular momentum is constant in magnitude but direction keeps changing.
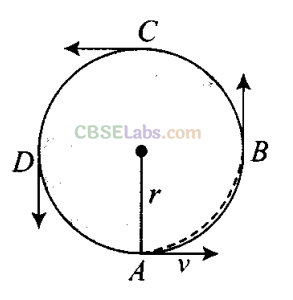
Sol: (a, b, c) While a particle is in uniform circular motion. Then the following statements are true.
(i) speed will be always constant throughout.
(ii) velocity will be always tangential in the direction of motion at a particular point.
(iii) the centripetal acceleration a = v2/r and its direction will always towards centre of the circular trajectory.
(iv) angular momentum (mvr) is constant in magnitude and direction. And its direction is perpendicular to the plane containing r and v.
Important point: In uniform circular motion, magnitude of linear velocity and centripetal acceleration is constant but direction changes continuously.
Very Short Answer Type Questions
Q16 .A cyclist starts from centre O of a circular park of radius 1 km and moves along the path OPRQO as shown in figure. If he maintains constant speed of 10 ms”1, what is his acceleration at point R in magnitude and direction?
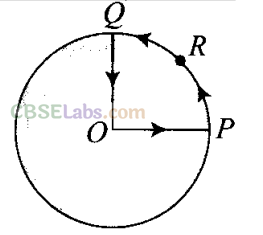
Ans: According to the problem the path of the cyclist is O-P- R-Q-O.
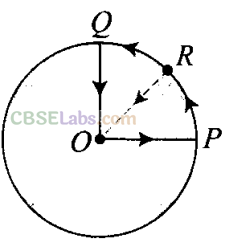
The cyclist is in uniform circular motion and it is given that linear velocity = 10 m/s, R = 1 km = 1000 m. As we know whenever an object is performing circular motion, acceleration is called centripetal acceleration and is always directed towards the centre.So cyclist experiences a centripetal force (acceleration) at point R towards centre.
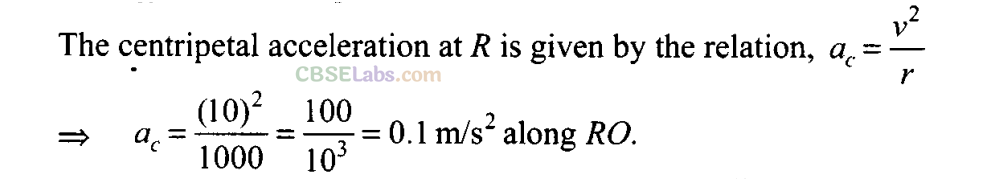
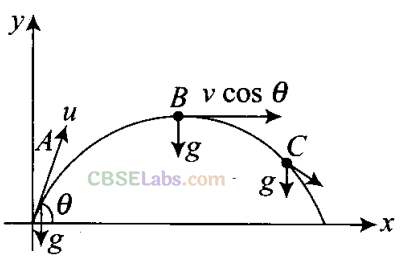
Q17. A particle is projected in air at some angle to the horizontal, moves along parabola as shown in figure where x and y indicate horizontal and vertical directions, respectively. Show in the diagram, direction of velocity and acceleration at points A, B and C.
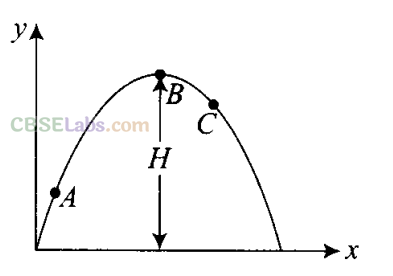
Sol: In projectile motion horizontal component of velocity will always be constant and acceleration is always vertically downward and is equal to g. Direction of velocity will always be tangential to the curve in the direction of motion.
As shown in the diagram in which a particle is projected at an angle 0.

Q18. A ball is thrown from a roof top at an angle
of 45° above the horizontal. It hits the ground a few seconds later. At what point during its motion, does the ball have
(a) greatest speed
(b) smallest speed
(c) greatest acceleration Explain.
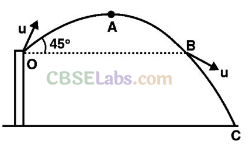
Ans: In this problem total mechanical energy of the ball is conserved. As the ball is projected from point O, and covering the path OABC.
At point A it has both kinetic and potential energy.
But at point C it have only kinetic energy, (keeping the ground as reference where PE is zero.)
(a) At point B, it will gain the same speed u and after that speed increases and will be maximum just before reaching C.
(b) During upward journey from OtoA speed decreases and smallest speed attained by it is at the highest point, i.e., at point A.
(c) Acceleration is always constant throughout the journey and is vertically downward equal to g.
Q19. A football is kicked into the air vertically upwards. What is its (a) acceleration and (b) velocity at the highest point?
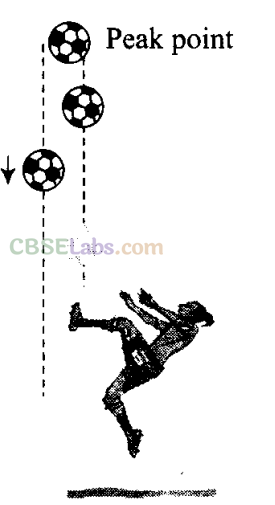
Sol: (a) The situation is shown in the diagram below in which a football is kicked into the air vertically upwards. Acceleration of the football will always be vertical downward and is called acceleration due to gravity (g).
(b) When the football reaches the highest point it is momentarily at rest and at that moment its velocity will be zero as it is continuously retarded by acceleration due to gravity (g).
Key concept: Collinear vectors: When the vectors under consideration can share the same support or have a common support then the considered vectors are collinear.
Coplanar vectors: Three (or more) vectors are called coplanar vector if they lie in the same plane. Two (free) vectors are always coplanar.

Q21. A boy travelling in an open car moving on a levelled road with constant speed tosses a ball vertically up in the air and catches it back. Sketch the motion of the ball as observed by a boy standing on the footpath. Give explanation to support your diagram.
Sol: With respect to the observer standing on the footpath ball is thrown with velocity u at an angle θ with the horizontal, hence it seems as a projectile. So path of the ball will be parabolic. The horizontal speed of the ball is same as that of the car, therefore, ball as well car travels equal horizontal ult distance. Due to its vertical speed, the ball follows a parabolic path.

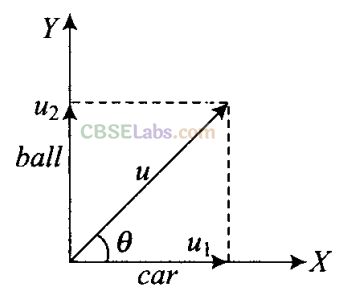
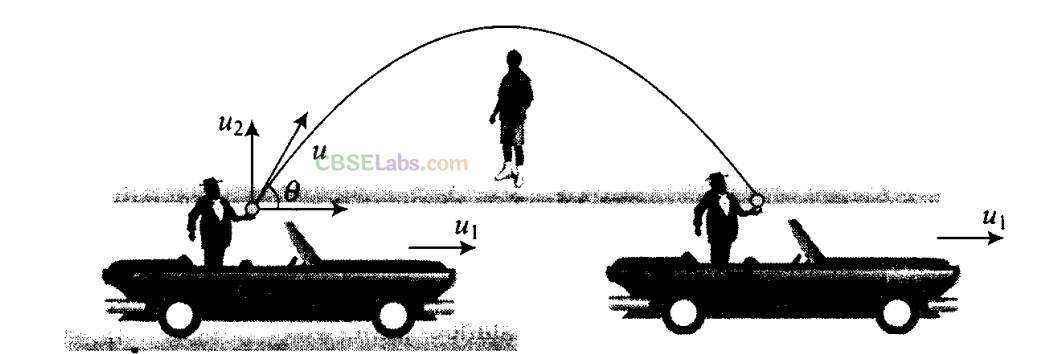
Important point: We must be very clear that we are working with respect to ground. When we observe with respect to the car, motion will be along vertical direction only.
Q22. A boy throws a ball in air at 60° to the horizontal along a road with a speed of 10 m/s (36 km/h). Another boy sitting in a passing by car observes the ball. Sketch the motion of the ball as observed by the boy in the car, if car has a speed of 18 km/h. Give explanation to support your diagram.
Sol: The situation is shown in the below diagram.
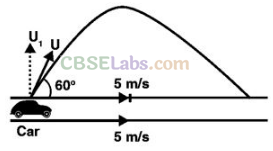
According to the problem the boy standing on ground throws the ball at an angle of 60° with horizontal at a speed of 10 m/s.
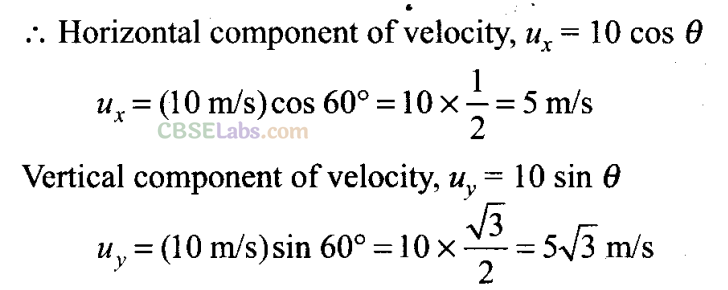
Speed of the car = 18 km/h = 5 m/s
As horizontal speed of ball and car is same, hence relative velocity of ball w.r.t car in the horizontal direction will be zero.
Only vertical motion of the ball will be observed by the boy in the car, as shown in above diagram.
Q23. In dealing with motion of projectile in air, we ignore effect of air resistance on motion. This gives trajectory as a parabola as you have studied. What would the trajectory look like if air resistance is included? Sketch such a trajectory and explain why you have drawn it that way.
Sol:
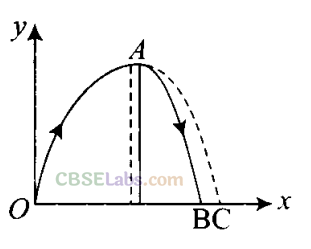
When we are dealing with projectile motion generally we neglect the air resistance. But if air resistance is included the horizontal component of velocity will not be constant and obviously trajectory will change.
Due to air resistance, particle energy as well as horizontal component of velocity keep on decreasing making the fall steeper than rise as shown in the figure.
When we are neglecting air resistance path was symmetric parabola (OAC). When air resistance is considered path is asymmetric parabola (OAB).
Short Answer Type Questions
Q24. A fighter plane is flying horizontally at an altitude of 1.5 km with speed 720 km/h. At what angle of sight (w.r.t. horizontal) when the target is seen, should the pilot drop the bomb in order to attack the target ?


2. When an object is dropped/released by any moving vehicle. Then initial velocity of the object is same as the moving vehicle.
When the bomb is dropped from Plane the plane which is moving horizontally. So, the bomb will have same initial velocity as that of plane along horizontal direction.
The situation is shown in the diagram below. Let a fighter plane, when it be plane at position P, drops a bomb to hit a target T.
Let the target is seen at an angle θ with horizontal.
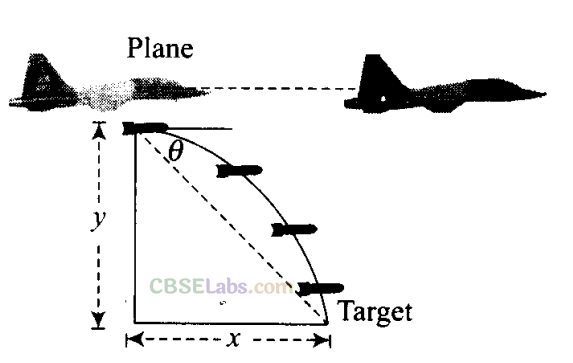

Important point: Angle is with respect to target. As seen by observer in the plane, motion of the bomb will be vertically downward below the plane. .
Q25. (a) Earth can be thought of as a sphere of radius 6400 km. Any object (or a person) is performing circular motion around the axis of the earth due to the earth rotation (period 1 day). What is the acceleration of object on the surface of the earth (at equator) towards its centre? What is it at latitude 9? How does these accelerations compare with g = 9.8 m/s2? (b) Earth also moves in circular orbit around the sun once every year with an orbital radius of 1.5 x 1011 What is the acceleration of the earth (or any object on the surface of the earth) towards the centre of the sun? How does this acceleration compare with g = 9.8 m/s2?


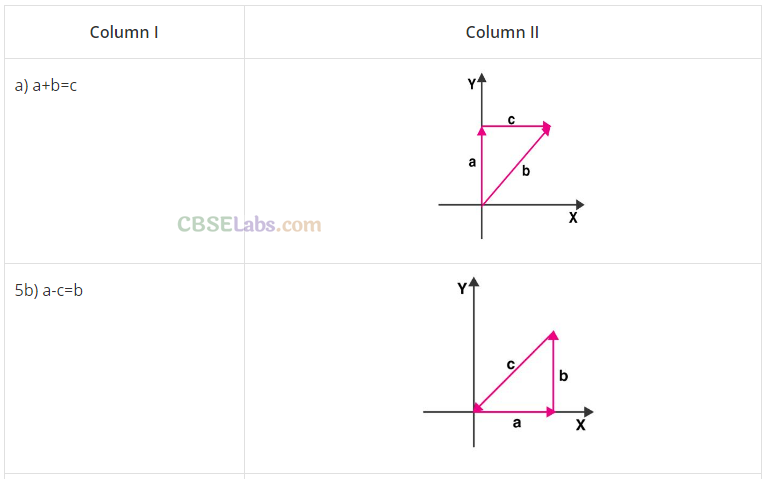
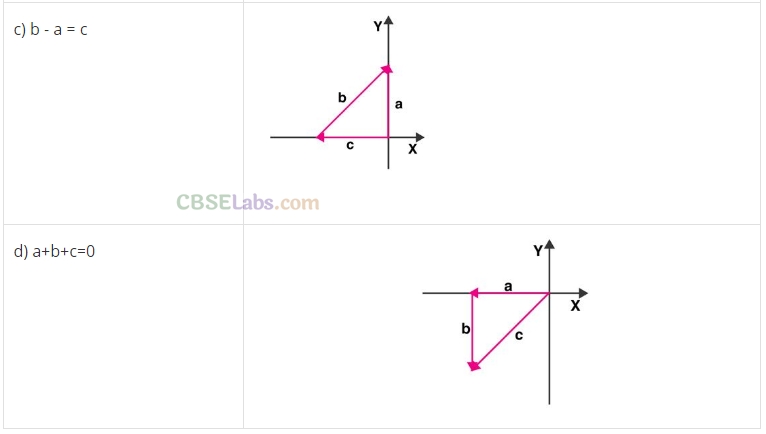
Q26. Given below in Column I are the relations between vectors a, b and c and in Column II are the orientations of a, b and c in the AY-plane. Match the relation in Column I to correct orientations in Column II.
Column I
(a) a + b = c
(b) a – c = b
(c) b – a = c
(d) a+b+c = 0
Column II
Sol: We apply triangulr law of addition
Triangular law of vector addition: Two vectors are considered as two sides of a triangle taken in the same order. The third side or completing side of the triangle is the resultant taken in the opposite order.
or
We can say that vectors are arranged head to tail, this graphical method is called the head-to-tail method. The two vectors and their resultant form three sides of a triangle, so this method is also known as triangle method of vector addition.
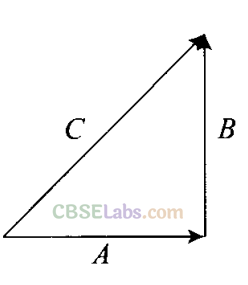
As shown in the diagram below in which vectors A and B are corrected by head and tail. Resultant vector C = A + B
(a) from (iv), it is clear that c = a + b
(b) from (iii), c + b = a => a- c = b
(c) from (i), b = a + c => b-a = c
(d) from (ii), -c = a + b => a + b + c = 0

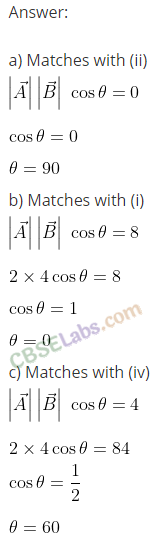
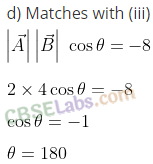

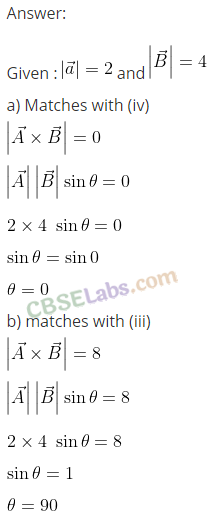
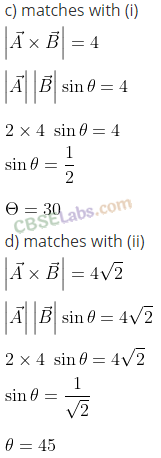
Long Answer Type Questions
Q29. A hill is 500 m high. Supplies are to be sent across the hill using a canon that can hurl packets at a speed of 125 m/s over the hill. The canon is located at a distance of 800 m from the foot of hill and can be moved on the ground at a speed of 2 m/s, so that its distance from the hill can be adjusted. What is the shortest time in which a packet can reach on the ground across the hill? Take g= 10 m/s2.
Sol.According to the problem, speed of packets =125 m/s , height of the hill = 500 m, distance between the cannon and the foot of the hill, d = 800 m
To cross the hill in shortest time, then the vertical component of the velocity should be minimum so that it just crosses the height of hill.
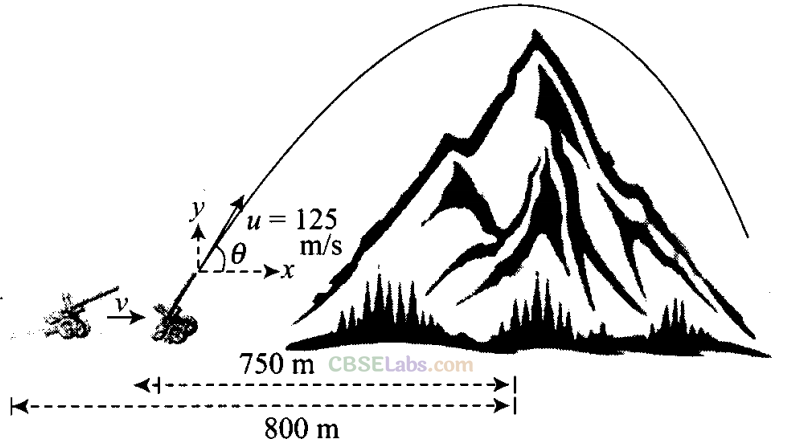
Distance through which canon has to be moved = 800 – 750 = 50 m Speed with which canon can move = 2 m/s


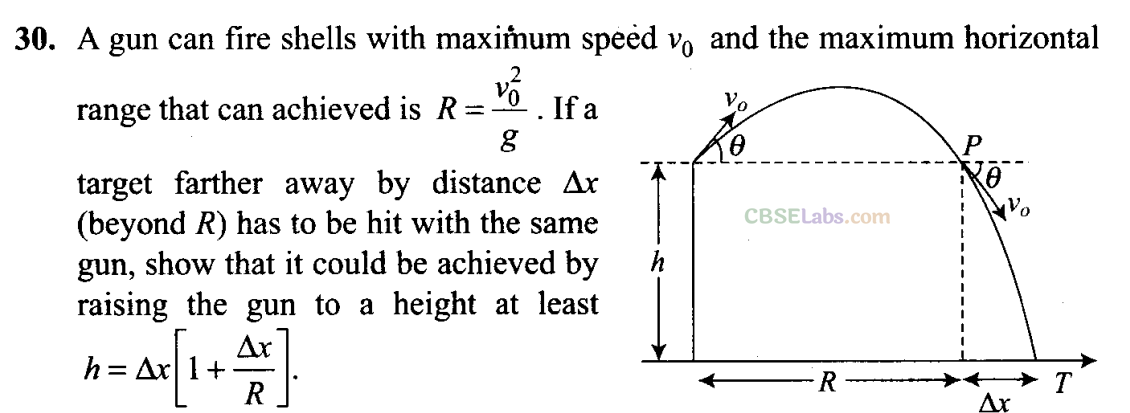


Important point: We should not confuse with the positive direction of motion. May be vertically upward direction or vertically downward direction is taken as positive according to convenience. And this problem can also be solved by taking motion from point P to T. From point P in the diagram projection at speed v0 at an angle θ below horizontal with height h and horizontal range ∆x. Then this will be analyzed from the alongside diagram
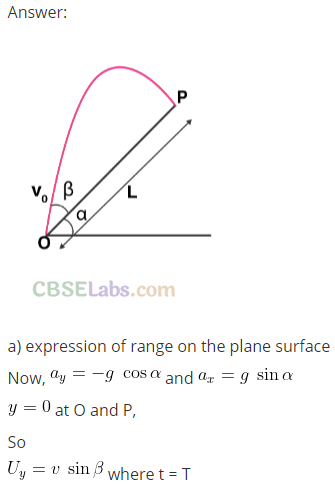
Q31. A particle is projected in air at an angle β to a surface which itself is inclined at an angle α to the horizontal (figure).
(a) Find an expression of range on the plane surface (distance on the plane from the point of projection at which particle will hit the surface).
(b) Time of flight.
(c) β at which range will be maximum
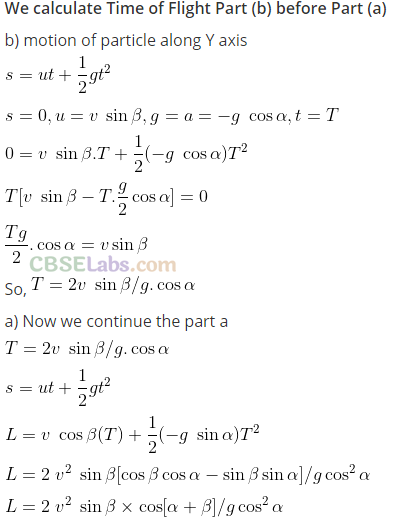
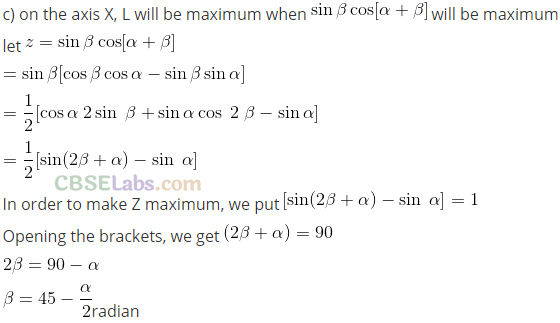
Q32. A particle falling vertically from a height hits a plane surface inclined to horizontal at an angle θ with speed v0 and rebounds elastically. Find the distance along the plane where it will hit second time.
Sol:

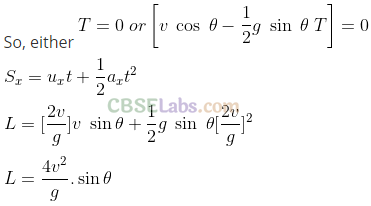
Q33. A girl riding a bicycle with a speed of 5 m/s towards north direction, observes rain falling vertically down. If she increases her speed to 10 m/s, rain appears to meet her at 45° to the vertical. What is the speed of the rain? In what direction does rain fall as observed by a ground based observer?
Sol: Vrgis the velocity of rain appears to the girl.
We must draw all vectors in the reference frame of ground-based observer.


Q34. A river is flowing due east with a speed 3 m/s. A swimmer can swim in still water at a speed of 4 m/s (figure).
(a) If swimmer, starts swimming due north, what will be his resultant velocity (magnitude and direction)?
(b) If he wants to start from point A on south bank –
and reach opposite point B on north bank,
(i) which direction should he swim?
(ii) what will be his resultant speed?
(c) From two different cases as mentioned in (a) and (b) above, in which case will he reach opposite bank in shorter time?
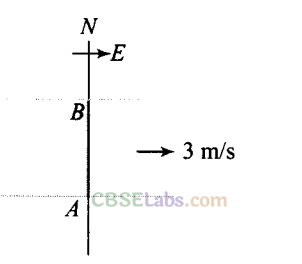
Sol:
Key concept: Analysis of Relative Velocity in Different Situations:
The motion of a boat (or a swimmer) in running water, say, a river.



Q32. A cricket fielder can throw the Cricket ball with a speed v0. If he throws the ball while running with speed u at an angle θ to the horizontal, find
(a) the effective angle to the horizontal at which the ball is projected in air as seen by a spectator.
(b) what will be time of flight?
(c) what is the distance (horizontal range) from the point of projection at which the ball will land?
(d) find θ at which he should throw the ball that would maximize the horizontal range as found in (c).
(e) how does θ for maximum range change if u > v0, u = v0, u < v0?
(f) how does θ in (e) compare with that for u = 0 (i.e., 45°)?
Sol:. The observer on ground (spectator) observes that the x-component of ball is more because of the speed of fielder. As shown in the adjacent diagram,
So, initial velocity in x-direction



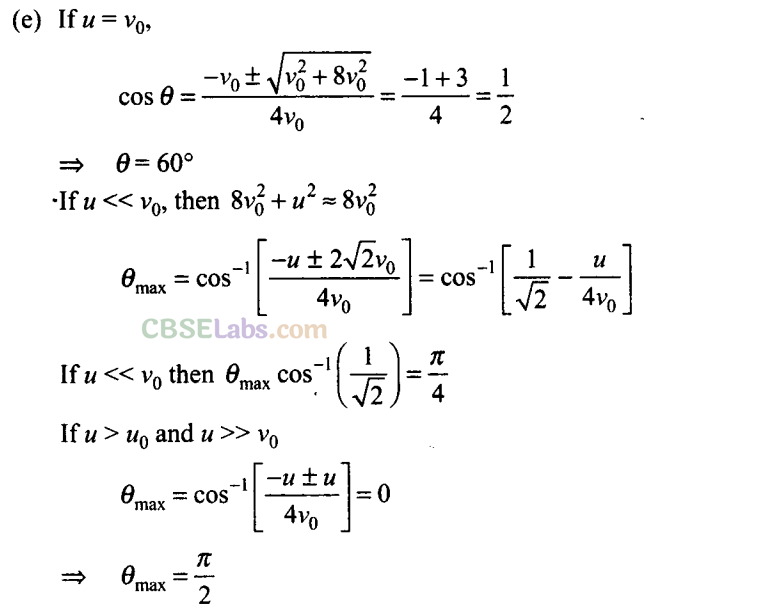
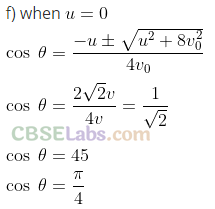




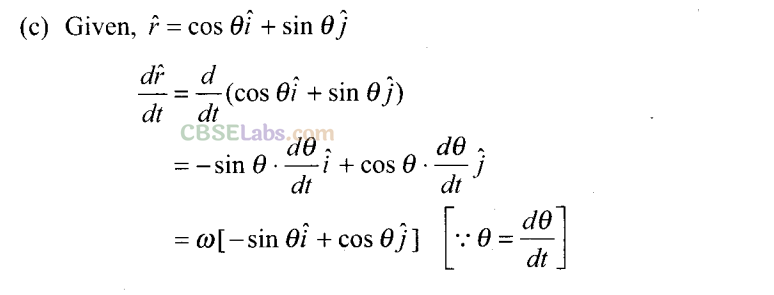

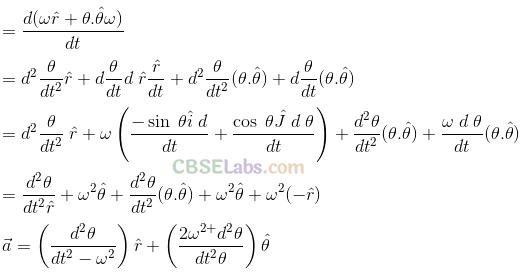
Q37. A man wants to reach from A to the opposite comer of the square C. The sides of the square are 100 m. A central square of 50 m x 50 m is filled with sand. Outside this square, he can walk at a speed 1 m/s. In the central square, he can walk only at a speed of v m/s (v < 1). What is smallest value of v for which he can reach faster via a straight path through the sand than any path in the square outside the sand?
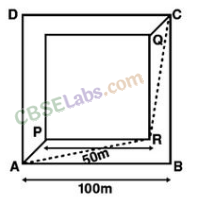
Solution:
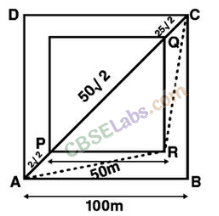

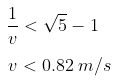
NCERT Exemplar Class 11 Physics Solutions
- Chapter 1 Units and Measurements
- Chapter 2 Motion in a Straight Line
- Chapter 3 Motion in a Plane
- Chapter 4 Laws of Motion
- Chapter 5 Work, Energy and Power
- Chapter 6 System of Particles and Rotational Motion
- Chapter 7 Gravitation
- Chapter 8 Mechanical Properties of Solids
- Chapter 9 Mechanical Properties of Fluids
- Chapter 10 Thermal Properties of Matter
- Chapter 11 Thermodynamics
- Chapter 12 Kinetic Theory
- Chapter 13 Oscillations
- Chapter 14 Waves
NCERT Exemplar ProblemsMathsPhysicsChemistryBiology
We hope the NCERT Exemplar Class 11 Physics Chapter 3 Motion in a Plane help you. If you have any query regarding NCERT Exemplar Class 11 Physics Chapter 3 Motion in a Plane, drop a comment below and we will get back to you at the earliest.