NCERT Exemplar Class 9 Science Chapter 11 Work and Energy are part of NCERT Exemplar Class 9 Science. Here we have given NCERT Exemplar Class 9 Science Solutions Chapter 11 Work and Energy.
NCERT Exemplar Class 9 Science Solutions Chapter 11 Work and Energy
Multiple Choice Questions
Question 1.
When a body falls freely towards the earth, then its total energy
(a) increases
(b) decreases
(c) remains constant
(d) first increases and then decreases
Solution:
(c) When a body falls freely towards the earth, its potential energy decreases which intum increases the kinetic energy. Therefore, its total energy remains constant.
Question 2.
A car is accelerated on a levelled road and attains a velocity 4 times of its initial velocity. In this process the potential energy of the car
(a) does not change
(b) becomes twice to that of initial
(c) becomes 4 times that of initial
(d) becomes 16 times that of initial
Solution:
(a) In the given process, the potential energy of the car does not change as it does not depend on velocity.
Question 3.
In case of negative work the angle between the force and displacement is
(a) 0°
(b) 45°
(c) 90°
(d) 180°
Solution:
(d) Work done is negative when force acts opposite to the direction of displacement, i.e. the angle between the two directions is 180°.
Question 4.
An iron sphere of mass 10 kg has the same diameter as an aluminium sphere of mass is 3.5 kg. Both spheres are dropped simultaneously from a tower. When they are 10 m above the ground, they have the same
(a) acceleration
(b) momenta
(c) potential energy
(d) kinetic energy
Solution:
(a) Both spheres have the same acceleration that is acceleration due to gravity g. Momenta, potential energy and kinetic energy depend on mass which is different for the two spheres and hence the quantities will differ for the two spheres.
Question 5.
A girl is carrying a school bag of 3 kg mass on her back and moves 200 m on a levelled road. The work done against the gravitational force will be (g =10 m s’2)
(a) 6×103 J
(b) 6 J
(c) 0.6 J
(d) zero
Solution:
(d) The gravitational force on the bag, i.e. the weight of bag is in vertically downward direction whereas the distance moved by her is in horizontal direction. It means that the force and displacement are perpendicular to each other, therefore no work is done.
Question 6.
Which one of the following is not the unit of energy?
(a) joule
(b) newton metre
(c) kilowatt
(d) kilowatt hour
Solution:
(c) Kilowatt is the unit of power, not of energy.
Question 7.
The work done on an object does not depend upon the
(a) displacement
(b) force applied
(c) angle between force and displacement
(d) initial velocity of the object
Solution:
(d) The work done on an object does not depend upon the initial velocity of the object.
Question 8.
Water stored in a dam possesses
(a) no energy
(b) electrical energy
(c) kinetic energy
(d) potential energy
Solution:
(d) Water stored in a dam possesses potential energy as it is stored at a certain height from the ground level.
Question 9.
A body is falling from a height h. After it has fallen a height \(\frac{h}{2}\), it will possess
(a) only potential energy
(b) only kinetic energy
(c) half potential and half kinetic energy
(d) more kinetic and less potential energy
Solution:
(c) When a body falls from a height \(\frac{h}{2}\) its potential energy becomes half (as potential energy = mgh ). The rest half of initial potential energy gets converted into kinetic energy.
Hence, the body will possess half potential energy and half kinetic energy.
Short Answer Type Questions
Question 10.
A rocket is moving up with a velocity v. If the velocity of this rocket is suddenly tripled, what will be the ratio of two kinetic energies?
Solution:
Let the mass of the rocket be m.
Kinetic energy of rocket when it moves with velocity v,
\(K_{1}=\frac{1}{2} m v^{2}\)
Kinetic energy of rocket when it moves with velocity 3v,
\(\begin{aligned} K_{2} &=\frac{1}{2} m(3 v)^{2} \\ &=\frac{9}{2} m v^{2} \\ \therefore \quad & \frac{K_{1}}{K_{2}}=\frac{\frac{1}{2} m v^{2}}{\frac{9}{2} m v^{2}}=\frac{1}{9} \\ \text { or } & K_{1} : K_{2}=1 : 9 \end{aligned}\)
Question 11.
Avinash can run with a speed of 8 m s-1 against the frictional force of 10 N, and Kapil can move with a speed of 3 ms-1 against the frictional force of 25 N. Who is more powerful and why?
Solution:
Since, Power = Force x Velocity
∴Power of Avinash, PA = 10 N x 8 m s-1= 80 W
Power of Kapil, PK= 25 N x 3 m s-1= 75 W
As PA > PK/ so, Avinash is more powerful than Kapil.
Question 12.
A boy is moving on a straight road against a frictional force of 5 N. After travelling a distance of 1.5 km he forgot the correct path at a round about as shown in figure of radius 100 m. However, he moves on the circular path for one and half cycle and then he moves forward upto 2.0 km. Calculate the work done by him.
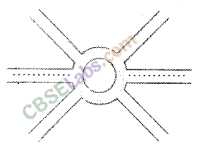
Solution:
Frictional force, F = 5 N As frictional force was always there in the motion of boy,
∴ Work done by boy = Force * Total distance covered
=5 N × [1.5 km+\(\frac { 3 }{ 2 }\)× 2× π × 0.1 km +2 km]
=5 N × 4.442 km
=5 N × 4442m=22210J
Question 13.
Can any object have mechanical energy even if its momentum is zero? Explain.
Solution:
Yes, if momentum of an object is zero, i.e.; p = mv =0
which gives v = 0 as m ≠ 0
Kinetic energy of the object =\(\frac { 1 }{ 2 }\)mv2= 0
Now, Mechanical energy = potential energy + kinetic energy (= 0) – potential energy (∴ K. E = 0)
So any object can have mechanical energy even if its momentum is zero.
Question 14.
Can any object have momentum even if its mechanical energy is zero? Explain.
Solution:
No, if mechanical energy = kinetic energy + potential energy = 0,
So, potential energy = kinetic energy = 0
or \(\frac { 1 }{ 2 }\)mv2= 0 or v = 0
So, momentum, p = mv = 0
Any object can not have momentum even if
its mechanical energy is zero.
Question 15.
The power of a motor pump is 2 kW. How much water per. minute the pump can raise to a height of 10 m? (Given g = 10m s-2)
Solution:
Here, power of motor pump, P = 2 kW
= 2000 W
Height to which water is raised, h = 10 m
As \(\frac { mgh }{ t } \) or \(\frac { pt }{ gh } \)
∴ Water raised per minute (= 60 s)
\(\frac { 2000\times 60 }{ 10\times 10 } =200\)
Question 16.
The weight of a person on a planet A is about half that on the earth. He can jump upto 0.4 m height on the surface of the earth. How high he can jump on the planet A?
Solution:
Weight of a person on a planet is half that on the earth,
WA=\(\frac { 1 }{ 2 }\)WE
or mgA = \(\frac { 1 }{ 2 }\) mgE
or gA = \(\frac { 1 }{ 2 }\)gE
Now, as the person jumps, gain in potential energy remains same.
So, mgAhA= mgEhE

=0.8m
(Using (i) and hE = 0.4 m)
Question 17.
The velocity of a body moving in a straight line is increased by applying a constant force F, for some distance in the direction of the motion. Prove that the increase in the kinetic energy of the body is equal to the work done by the force on the body.
Solution:
Let the body covers a distance s when a constant force F is applied in the direction of motion.
Work done by this force, W=F . s
Let the velocity of object of mass m change
from u to v with acceleration a on application
of constant force F, then F = ma
From equation of motion, v2-u2 = 2as, we get
\(\frac s=\frac{v^{2}-u^{2}}{2 a}\)
∴W=Fs=ma\(\left(\frac{v^{2}-u^{2}}{2 a}\right)\)
=\(\frac { 1 }{ 2 }\)mv2-\(\frac { 1 }{ 2 }\)mu2
= final kinetic energy – initial kinetic energy
= change in kinetic energy
Question 18.
Is it possible that an object is in the state of accelerated motion due to external force acting on it, but no work is being done by the force. Explain it with an example.
Solution:
Yes, it is possible that an object is in the state of accelerated motion due to external force acting on it, but no work is being done by the force.
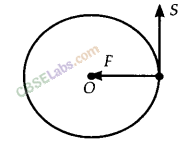
For example, an object moving in a circular path due to centripetal force acting on it.
At any instant of time, a constant acceleration due to the centripetal force act on the object along the radius towards the centre while the direction of displacement is tangential to the circle. That is, force and displacement are perpendicular to each other and hence no work is being done.
Question 19.
A ball is dropped from a height of 10 m. If the energy of the ball reduces by 40% after striking the ground, how much high can the ball bounce back? (g = 10 m s-2)
Solution:
Let the mass of the ball be m, then, initial potential energy of the ball
= mgh = 10 x 10 x m
=100 m J
Since the energy of the ball reduces by 40% after striking the ground, energy left with the ball = 60% of P.E.
=\(\frac { 60 }{ 100 }\) x 100 m = 60 m J
Let the ball bounce back to height W due to this remaining energy,
∴ mgh = 60 m
h=\(\frac { 160m }{ mg }\)=6m
Question 20.
If an electric iron of 1200 W is used for 30 minutes everyday, find electric energy consumed in the month of April.
Solution:
Power of electric iron, P = 1200 W Time for which it is used in one day, t = 30 min
= 30 x 60 s = 1800 s
Energy consumed in one day = P x t
= 1200 W x 1800 s
= 2.16 x 106 J
As there are 30 days in April, so energy consumed in the month of April = 2.16 x 106 x 30 J
= 6.48 x 107 J
Long Answer Type Questions
Question 21.
A light and a heavy object have the same momentum. Find out the ratio of their kinetic energies. Which one has a larger kinetic energy?
Solution:
Let m and M be the masses of a light and a heavy object moving with velocities v and V respectively.
As both have the same momentum,
∴ mv = MV
or \(\frac { M }{ V }\) …(i)
Kinetic energy of light object,
\(K_{m}=\frac{1}{2} m v^{2}\)
Kinetic energy of heavy object,
\(K_{m}=\frac{1}{2} m V^{2}\)
Kinetic energy of heavy object,
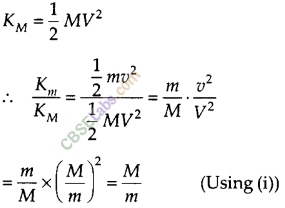
As M>m;
Km > KM, i.e. light object has larger kinetic energy.
Question 22.
An automobile engine propels a 1000 kg car (A) along a levelled road at a speed of 36 km h ’. Find the power if the opposing frictional force is 100 N. Now, suppose after travelling a distance of 200 m, this car collides with another stationary car (8) of same mass and comes to rest. Let its engine also stop at the same time. Now car (B) starts moving on the same level road without getting its engine started. Find the speed of the car (6) just after the collision.
A light and a heavy object have the same momentum. Find out the ratio of their kinetic energies. Which one has a larger kinetic energy?
Solution:
Here, mass of the car A, mA = 1000 kg
Initial speed of the car A, uA = 36 km h_1
= 36 x \(\frac { 5 }{ 18 }\)= 10m s-1
Opposing frictional force, F = 100 N
∴ Power of the engine of car A
= F µA = (100 N) x (10 m s-1) = 1000 W
When car A collides with car B of mass 1000 kg,
Final speed of car A, vA = 0
Initial speed of car B, uB = 0
Applying conservation of momentum, P, = P,
mAvA + mBuB = mAvA + mBvB
1000 x 10 + 1000 x 0 = 1000 x o + 1000 x vB
∴vB = 10m s-1
So, the speed of the car B just after collision is 10m s-1
Question 23.
A girl having mass of 35 kg sits on a trolley of mass 5 kg. The trolley is given an initial velocity of 4 10m s-1 by applying a force. The trolley comes to rest after traversing a distance of 16 m.
(a) How much work is done on the trolley?
(b) How much work is done by the girl?
Solution:
Effective mass of girl + trolley system = mass of girl + mass of trolley = 35 kg + 5 kg = 40 kg
Here, u = 4 10m s-1, v – 0, s = 16 m
Using v2 – u2= 2as, we get
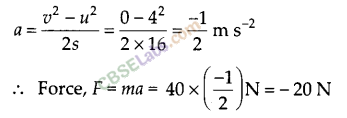
(a) Work done on the trolley = – Work done by the trolley
= -Fs
= – (-20 N) x (16 m)
= 320 J
(b) As the girl keeps sitting on the trolley, there is no displacement in her position with respect to trolley, so no work is done by the girl.
Question 24.
Four men lift a 250 kg box to a height of 1 m and hold it without raising or lowering it.
(a) How much work is done by the men in lifting the box?
(b) How much work do they do in just holding it?
(c) Why do they get tired while holding it? (g = 10 m s-2)Solution:
Mass of the box, m = 250 kg
Height upto which it is raised, h = 1 m
(a) Work done by the men in lifting the box
= F.s = 250 x 10 x 1 J
(Here F = mg, s = h)
= 2500 J
(b) In just holding the box, there is no displacement, so no work is done.
(c) In order to hold the box at a certain height, men are applying a force which is equal and opposite to the gravitational force acting on the box. While applying the force, muscular effort is involved.
So, men get tired while holding it.
Question 25.
What is power? How do you differentiate ’ kilowatt from kilowatt hour? The Jog Falls in
Karnataka state are nearly 20 m high. 2000 tonnes of water falls from it in a minute. Calculate the equivalent power if all this energy can be p utilized? (g = 10 m s-2)
Solution:
Power is defined as the rate of doing work or the rate of transfer of energy, Kilowatt is the unit of power and kilowatt hour is the unit of energy or work as kilowatt hour = unit of power x unit of time.
Energy possessed by 2000 tonnes
(= 2000 x 103 kg) water at a height of 20 m, Ef, = mgh
= 2000 x 103 x 10 x 20
= 4 x 108 J
Power generated if all this energy can be
utilized,

Question 26.
How is the power related to the speed at which a body can be lifted? How many kilograms will a man working at the power of 100 W, be able to lift at constant speed of 1 m s’1 vertically? (g=10ms~2) ,
Solution:
Power associated in lifting a body of mass m upto a height h in time t is,
p=\(\frac { mgh }{ t }\)
Here, \(\frac { h }{ t }\) = speed = v
∴ P=mgv
Here P = 100W, v=1ms-1,10 ms-2
m=\(\frac { P}{ gv }\)
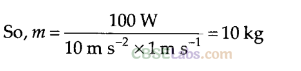
Question 27.
Define watt. Express kilowatt in terms of joule per second. A 150 kg car engine develops 500 W for each kg. What force does it exert in moving the car at a speed of 20 m s’1?
Solution:
One watt is the power of an agent which does work at the rate of one joule per second. 1 kilowatt = 1000 watt
= 1000 joule per second (v 1 W = 1 J s-1)
Mass of the car, m = 150 kg
Power developed by engine per kg = 500 W
Total power developed by engine,
P = 500 W x 150
= 75000 W
Speed of car, v = 20 m s_1 Power, P = Fv
=> Force exerted in moving the car, f = \(\frac { P}{ v }\)
=\(\frac{75000 \mathrm{W}}{20 \mathrm{ms}^{-1}}\)
=3750 N
Question 28.
Compare the power at which each of the following is moving upwards against the force of gravity? (given g =10m s-2)
- a butterfly of mass 1.0 g that flies upward at a rate of 0.5 m s1.
- a 250 g squirrel climbing up on a tree at a rate of 0.5 m s-1.
Solution:
- Mass of butterfly, mb= 1 g = 10-3 kg
Speed, vb = 0.5 m s-1
Force of gravity on butterfly, Fh = mbg
= 10-3 x 10 = 10-2 N
Power, Pb = Fb.vb = 10-2 N x 0.5 m s-1 = 0.005 W - Mass of squirrel, ms = 250 g = 0.25 kg
Speed, vs = 0.5 m s-1
Force of gravity on squirrel,
Fs = msg = 0.25 x 10 = 2.5 N
Power, Ps = Fs.vs= 2.5 N x 0.5 m s-1 = 1.25 W
Hence, the squirrel exerts more power in climbing than a butterfly exerts in flying at the same rate.
NCERT Exemplar Class 9 Science Solutions
- Chapter 1 Matter In Our Surroundings
- Chapter 2 Is Matter Around Us Pure
- Chapter 3 Atoms and Molecules
- Chapter 4 Structure of the Atom
- Chapter 5 The Fundamental Unit of Life
- Chapter 6 Tissues
- Chapter 7 Diversity in Living Organisms
- Chapter 8 Motion
- Chapter 9 Force and Laws of Motion
- Chapter 10 Gravitation
- Chapter 11 Work and Energy
- Chapter 12 Sound
- Chapter 13 Why do we Fall ill
- Chapter 14 Natural Resources
- Chapter 15 Improvement in Food Resources
We hope the NCERT Exemplar Class 9 Science Chapter 11 Work and Energy will help you. If you have any query regarding NCERT Exemplar Class 9 Science Solutions Chapter 11 Work and Energy, drop a comment below and we will get back to you at the earliest.