Applications of Trigonometry: Trigonometry is the branch of mathematics deals with triangles involved with the study of lengths, heights, and angles. Trigonometry and its functions have an enormous number of uses in our real life.
Applications of Trigonometry
You have studied in social studies that the highest mountain peak in the world is Mount Everest and its height is 8848 meters.
Kuntala waterfall in Adilabad district is the highest natural waterfall in Andhra Pradesh. Its height is 147 feet.
How were these heights measured? Can you measure the height of your school building or the tallest tree in or around your school?
Let us understand through some examples. Vijaya wants to find the height of a palm tree. She tries to locate the
top most point of the tree. She also imagines a line joining the top most point and her eye.
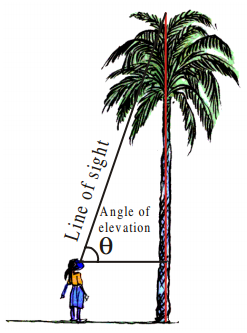
This line is called “line of sight”. She also imagines a horizontal line, parallel to earth, from her eye to the tree.
Here, “the line of sight”, “horizontal line” and “the tree” form a right angle triangle.
To find the height of the tree, she needs to find a side and an angle in this triangle.
“The line of sight is above the horizontal line and angle between the line of sight and the horizontal line is called angle of elevation”.
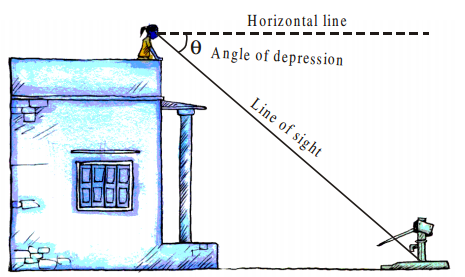
Suppose you are standing on the top of your school building and you want to find the distance of borewell from the
building on which you are standing. For that, you have to observe the base of the borewell. Then, the line of sight from your eye to the base of borewell is below the horizontal line from your eye. Here, “the angle between the line of sight and horizontal line is called angle of depression.”
Trigonometry has been used by surveyors for centuries. They use Theodolites to measure angles of elevation or depression in the process of survey. In nineteenth century, two large Theodolites were built by British India for the surveying project“great trigonometric survey”. During the survey in 1852, the highest mountain peak in the world was discovered in the Himalayas. From the distance of 160 km, the peak was observed from six different stations and the height of the peak was calculated. In 1856, this peak was named after Sir George Everest, who had commissioned and first used the giant Theodolites. Those theodolites are kept in the museum of the Survey of India in Dehradun for display.
Drawing Figures to Solve Problems
When we want to solve the problems of heights and distances, we should consider the following:
- All the objects such as towers, trees, buildings, ships, mountains etc. shall be considered as linear for mathematical convenience.
- The angle of elevation or angle of depression is considered with reference to the horizontal line.
- The height of the observer is neglected, if it is not given in the problem.
When we try to find heights and distances at an angle of elevation or depression, we need to visualise geometrically. To find heights and distances, we need to draw figures and with the help of these figures we can solve the problems. Let us see some examples.
Trigonometry in Real Life:
- Electric poles are present everywhere. They are usually erected by using a metal wire. The pole, wire and the ground form a triangle. But, if the length of the wire decreases, what will be the shape of the triangle and what will be the angle of the wire with the ground ?

- A person is whitewashing a wall with the help of a ladder which is kept as shown in the adjacent figure on
left. If the person wants to paint at a higher position, what will the person do? What will be the change in angle of the ladder with the ground ?

- In the temple at Jainath in Adilabad district, which was built in 13th century, the first rays of the Sun fall at the feet of the Idol of Suryanarayana Swami in the month of December. There is a relation between distance of Idol from the door, height of the hole on the door from which Sun rays are entering and angle of sun rays in that
month. Is there any triangle forming in this context? - In a play ground, children like to slide on slider and slider is on a defined angle from earth. What will happen to the slider if we change the angle? Will children still be able to play on it?
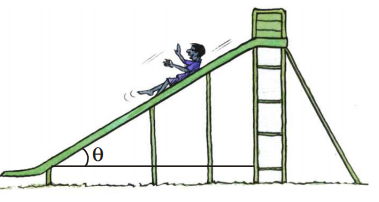
The above examples are geometrically showing the application part of triangles in our daily life and we can measure the heights, distances and slopes by using the properties of triangles. These types of problems are part of ‘trigonometry’ which is a branch of mathematics.
Now look at the example of a person who is white washing the wall with the help of a ladder as shown in the previous figure. Let us observe the following conditions.
We denote the foot of the ladder by A and top of it by C and the point of joining height of the wall and base of the ladder as B. Therefore, ∆ABC is a right angle triangle with right angle at B. The angle between ladder and base is said to be θ.
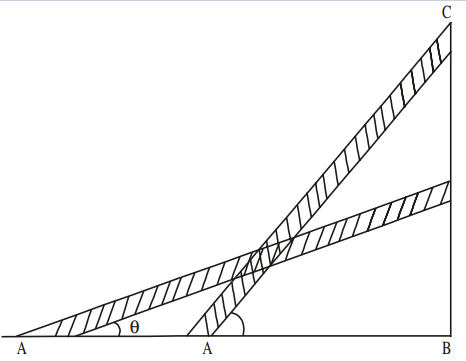
- If the person wants to white wash at a higher point on the wall-
● What happens to the angle made by the ladder with the ground?
● What will be the change in the distance AB? - If the person wants to white wash at a lower point on the wall-
● What happens to the angle made by the ladder with the ground?
● What will be the change in the distance AB?
We have observed in the above example of a person who was white washing. When he wants to paint at higher or lower points, he should change the position of ladder. So, when ‘θ’ is increased, the height also increases and the base decreases. But, when θ is decreased, the height also decreases and the base increases. Do you agree with this statement?
Here, we have seen a right angle triangle ABC and have given ordinary names to all sides and angles. Now let’s name the sides again because trigonometric ratios of angles are based on sides only
It may not have direct applications in solving practical issues but used in the various field. For example, trigonometry is used in developing computer music: as you are familiar that sound travels in the form of waves and this wave pattern through a sine or cosine function for developing computer music. Here are few applications where trigonometry and its functions are applicable. Trigonometric and its functions are applicable to measure the height of a building or a mountain, video games, constructions, aviation, physics, criminology, marine biology, marine engineering and navigation.
The calculus is based on trigonometry and algebra. The fundamental trigonometric functions like sine and cosine are used to describe the sound and light waves, Trigonometry uses in oceanography to calculate heights of waves and tides in oceans, creation of maps and satellite systems.
Thus here we have discussed Trigonometry and its importance as every student of math is expected to know about the application of this branch of mathematics in daily life. Solve sample questions with answers and cross check your answers with the NCERT Solutions on some applications of Trigonometry.