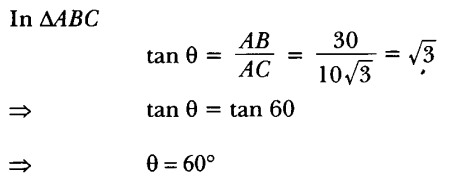Height and Distance: One of the main application of trigonometry is to find the distance between two or more than two places or to find the height of the object or the angle subtended by any object at a given point without actually measuring the distance or heights or angles. Trigonometry is useful to astronomers, navigators, architects and surveyors etc. in solving problems related to heights and distances.
Height and Distance
The directions of the objects can be described by measuring:
- Angle of elevation
- Angle of depression
Angles of elevation or angles of depression of the objects are measured by an instrument called Theodolite. Theodolite is based on the principles of trigonometry, which is used for measuring angles with a rotating telescope. In 1856, Sir George Everest first used the giant theodolite, which is now on display in the Museum of the survey of India in Dehradun
Angle of Elevation
Let P be the position of the object above the horizontal line OA and O be the eye of the observer, then angle AOP is called angle of elevation. It is called the angle of elevation, because the observer has to elevate (raise) his line of sight from the horizontal OA to see the object P. [When the eye turns upwards above the horizontal line].
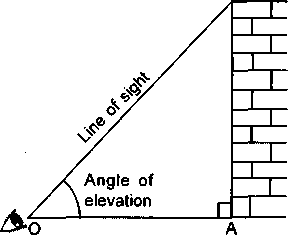
Line of sight: It is the line drawn from the eye of an observer to the object viewed.
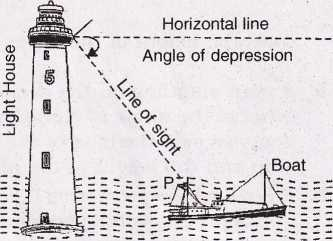
Angle of Depression
Let P be the position of the object below the horizontal line OA and O be the eye of the observer, then angle AOP is called angle of depression.
It is called the angle of depression because the observer has to depress (lower) his line of sight from the horizontal OA to see the object P.
[When the eye turns downwards below the horizontal line].
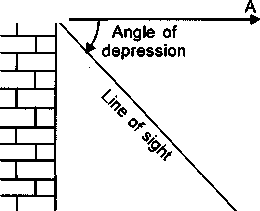
Below the eye level: If the object lies below the horizontal plane of our eyes, then we have to move our head downwards to view it. In doing so, our lines of sight moves downwards through an angle and the angle, which the line of sight now makes with the horizontal line, is called the angle of depression of the object from our eyes.
Example : Let OH be the horizontal line at the eye level. If a person at O looks at an object P lying below the eye level, then, ∠HOP is the angle of depression of P as seen from O.
Note : Angle of depression of P as seen from O = angle of elevation of O, as seen from P.
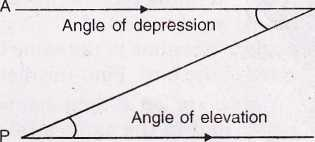
∴ ∠AOP = ∠OPH
Height and Distance Formulas
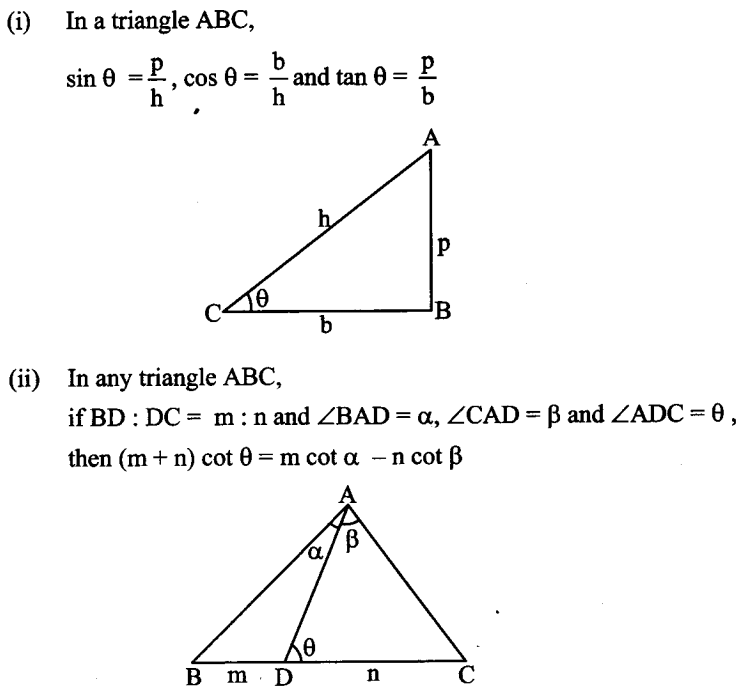
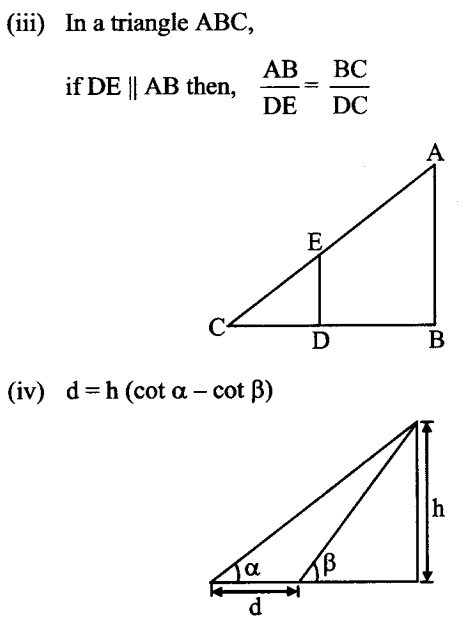
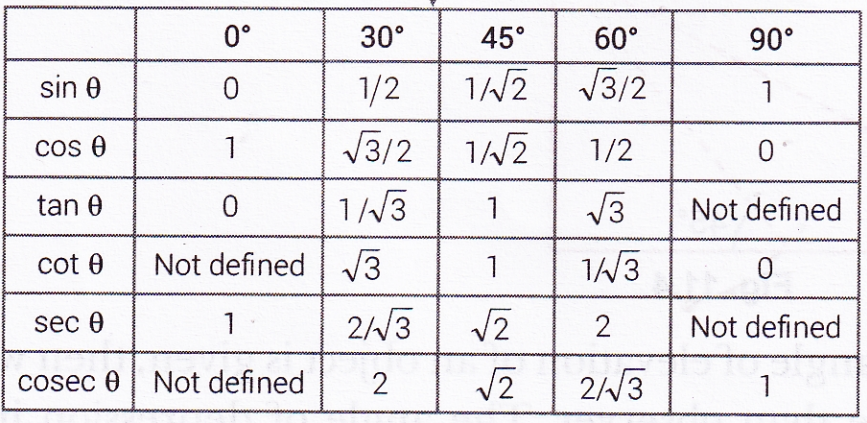
Trigonometry Ratios Table
Height and Distance Important Points
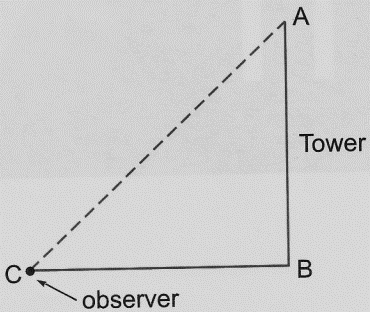
- In solving problems observer is represented by a point if his height is not given.
- In solving problems object is represented by a line segment and some times by a point if height or length is not considered.
For example, AB is tower and point C is observer.
- A line drawn parallel to earth surface is called horizontal line.
- The angle of elevation and depression are always acute angles.
- If the observer moves towards the objects like tower, building, cliff, etc. then angle of elevation increases and if the observer moves away from the object, the angle of elevation decreases.
- If the angle of elevation of sun decreases, then the length of shadow of an object increases and vice-versa.
- If in problems, the angle of elevation of an object is given, then we conclude that the object is at higher altitude than observer. The angle of depression implies that observer is at higher altitude than object.
Height and Distance Questions
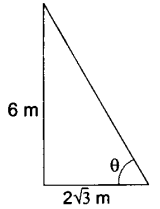
1. If a pole 6 m high casts a shadow 2√3 m long on the ground, find the Sun’s elevation. [ NCERT Exemplar]
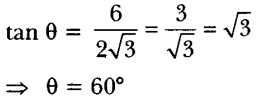
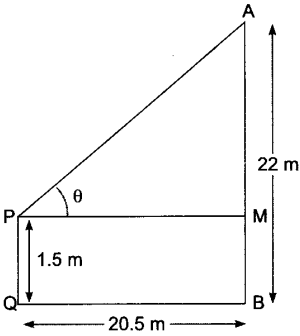
2. An observer 1.5 m tall is 20.5 m away from a tower 22 m high. Determine the angle of elevation of the top of the tower from the eye of the observer.
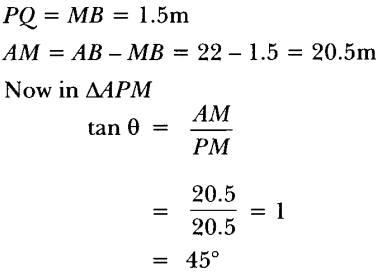
3. A ladder 15 m long makes an angle of 60o with the wall. Find the height of the point where the ladder touches the wall. [CBSE (F) 2017]
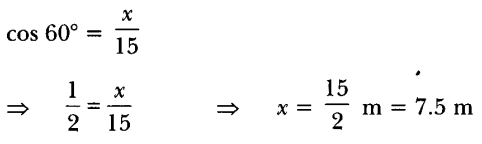
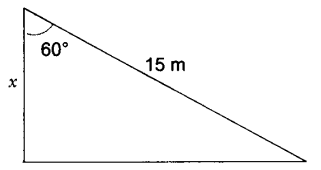
4. The ratio of the height of a tower and the length of its shadow on the ground is √3 : 1. What is the angle of elevation of the sun? [CBSE Delhi 2017]
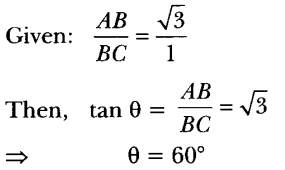
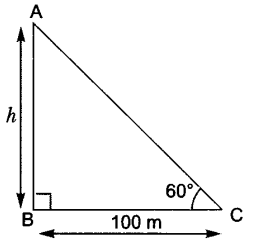
5. If the angle of elevation of a tower from a distance of 100 m from its foot is 60°, then what will be the height of the tower? [NCERT Exemplar]
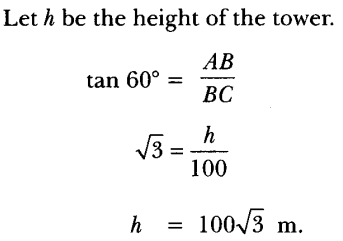
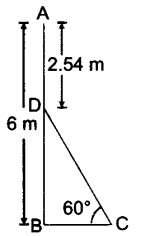
6. In Fig. 11.10, AB is a 6 m high pole and CD is a ladder inclined at an angle of 60° to the horizontal and reaches up to a point D of pole. If AD = 2.54 m, find the length of the ladder, (use √3 =1.73) [CBSE Delhi 2016]
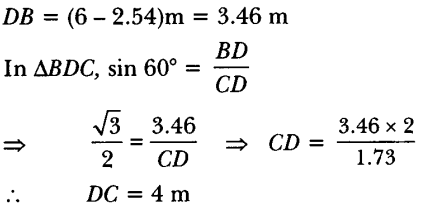
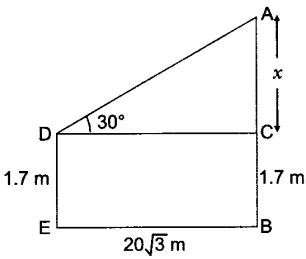
7. An observer, 1.7 m tall, is 20 √3 m away from a tower. The angle of elevation from the eye of observer to the top of tower is 30°. Find the height of tower. [CBSE (F) 2016]
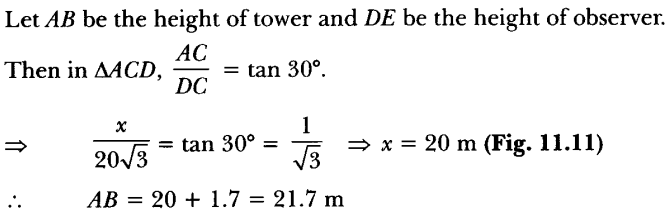
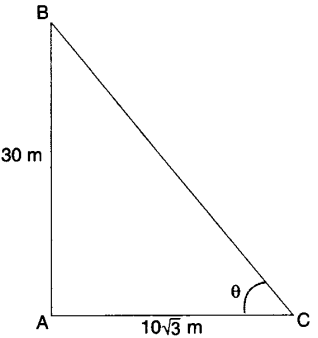
8. If a tower 30 m high, casts a shadow 10 √3 m long on the ground, then what is the angle of elevation of the sun ? [CBSE (AI) 2017]