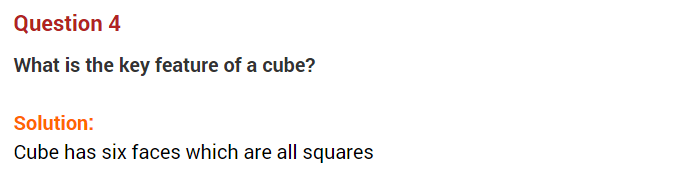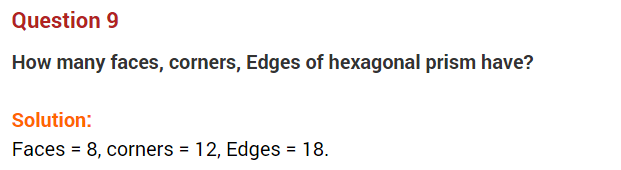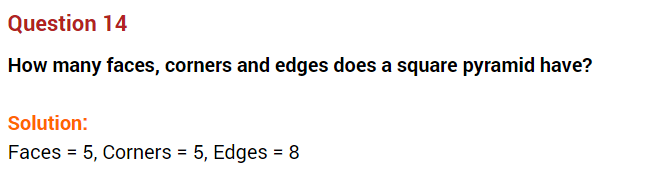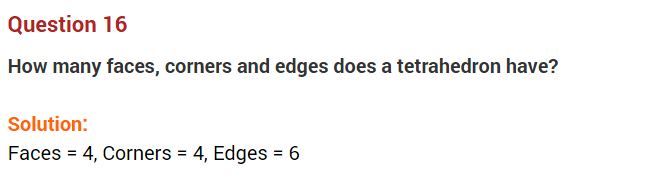Visualising Solid Shapes Class 8 Extra Questions Maths Chapter 10
Extra Questions for Class 8 Maths Chapter 10 Visualising Solid Shapes
Visualising Solid Shapes Class 8 Extra Questions Very Short Answer Type
Question 1.
Draw any four 3-dimensional figures.
Solution:

Question 2.
Verify Euler’s formula for a right triangular prism.

Solution:
Number of vertices (V) = 6
Number of faces (F) = 5
and number of edges (E) = 9
Euler’s formula:
V + F – E = 2
⇒ 6 + 5 – 9 = 2
⇒ 2 = 2
Hence, the formula is verified.
Question 3.
Find the number of vertices of hexagonal prisms.
Solution:
Number of vertices = 2 × Number of sides = 2 × 6 = 12
Question 4.
Verify whether a polyhedron can have 10 faces, 20 edges and 15 vertices.
Solution:
We have
Number of faces F = 10
Number of edges E = 20
and number of vertices V = 15
Euler’s formula:
V + F – E = 2
⇒ 15 + 10 – 20 = 2
⇒ 5 ≠ 2
Hence, it is not possible to have a polyhedron satisfying the above data.
Question 5.
If F = 18 and V = 10, then find the value of E in Euler’s formula.
Solution:
We know that
V + F – E = 2
⇒ 10 + 18 – E = 2
⇒ 28 – E = 2
⇒ E = 28 – 2 = 26
Hence, the required value of E = 26
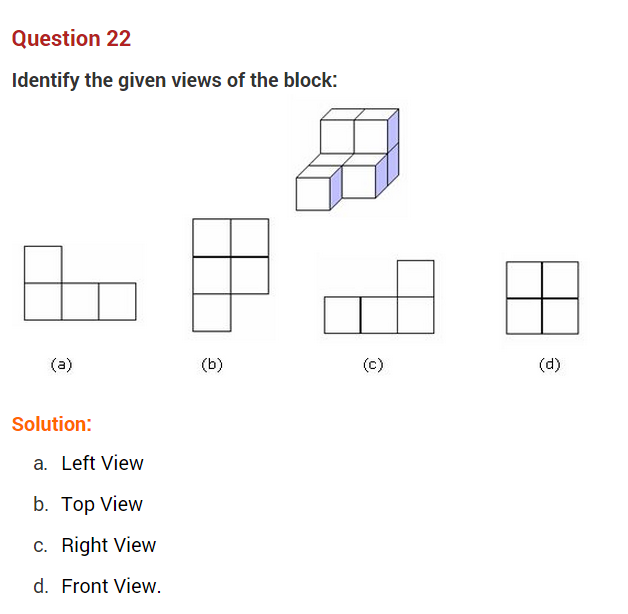
Question 6.
Draw the front, side and top views of the following 3-D figures.

Solution:

Question 7.
Draw the nets of the following polyhedrons.
(i) Cuboid
(ii) Triangular prism with a base equilateral triangle.
(iii) Square pyramid.
Solution:
(i) The net pattern of cuboid

(ii) The net pattern of a triangular prism

(iii) Net pattern of square pyramid

Question 8.
The given net is made up of two equilateral triangles and three rectangles.

(i) Name the solid it represents.
(ii) Find the number of faces, edges and vertices.
Solution:
(i) The given figure represents the net prims of the triangular prism
(ii) Number of faces = 5
Number of edges = 9
Number of vertices = 6
Visualising Solid Shapes Class 8 Extra Questions Short Answer Type
Question 9.
Match the following:

Solution:
(a) → (vi)
(b) → (v)
(c) → (ii)
(d) → (i)
(e) → (iii)
(f) → (v)
Question 10.
Using Euler’s formula, fill in the blanks:
| Faces | Vertices | Edges | |
| (a) | 6 | 8 | — |
| (b) | — | 10 | 15 |
| (c) | 4 | — | 6 |
| (d) | 5 | 6 | — |
| (e) | 8 | 12 | — |
| (f) | 7 | 7 | — |
Solution:
(a) F + V – E = 2
⇒ 6 + 8 – E = 2
⇒ 14 – E = 2
⇒ E = 14 – 2 = 12
(b) F + V – E = 2
⇒ F + 10 – 15 = 2
⇒ F – 5 = 2
⇒ F = 2 + 5 = 7
(c) F + V – E = 2
⇒ 4 + V – 6 = 2
⇒ V – 2 = 2
⇒ V = 2 + 2 = 4
(d) F +V – E = 2
⇒ 5 + 6 – E = 2
⇒ 11 – E = 2
⇒ E = 11 – 2 = 9
(e) F + V – E = 2
⇒ 8 + 12 – E = 2
⇒ 20 – E = 2
⇒ E = 20 – 2 = 18
(f) F + V – E = 2
⇒ 7 + 7 – E = 2
⇒ 14 – E = 2
⇒ E = 14 – 2 = 12
Hence (a) → 12, (b) → 7, (c) → 4, (d) → 9, (e) → 18, (f) → 12
Question 11.
Name the solids that have:
(i) 4 faces
(ii) 8 triangular faces
(iii) 6 faces
(iv) 1 curved surface
(v) 5 faces and 5 vertices
(vi) 6 rectangular faces and 2 hexagonal faces
Solution:
(i) Tetrahedron
(ii) Regular octahedron
(iii) Cube and cuboid
(iv) Cylinder
(v) Square and a rectangular pyramid
(vi) Hexagonal prism
Question 12.
Complete the table:
| Solid | F | V | E | F + V | E + 2 |
| Cuboid | — | — | — | — | — |
| Triangular pyramid |
— | — | — | — | — |
|
Triangular prism |
— | — | — | — | — |
| Pyramid with square base | — | — | — | — | — |
| Prism with square base | — | — | — | — | — |
Solution:
| Solid | F | V | E | F + V | E + 2 |
| Cuboid | 6 | 8 | 12 | 14 | 14 |
| Triangular pyramid |
4 | 4 | 6 | 8 | 8 |
|
Triangular |
5 | 6 | 9 | 11 | 11 |
| Pyramid with square base | 5 | 5 | 8 | 10 | 10 |
| Prism with square base | 6 | 8 | 12 | 14 | 14 |
Question 13.
Use isometric dot paper to sketch a rectangular prism with length 4 units, height 2 units and width 3 units. (NCERT Exemplar)
Solution:
Steps:
1. Draw a parallelogram with sides 4 units and 3 units. This is the top of the prism (Fig. 1).

2. Start at one vertex. Draw a line passing through two dots. Repeat for the other three vertices. Draw the hidden edges as a dashed line (Fig. 2).

3. Connect the ends of the lines to complete the prism (Fig. 3).