Six trigonometric ratios for right angle triangle are Sine(sin), Cosecant(Cos), Tangent(Tan), Cosecant(Cos), Secant(Sec), Cotangent(Cot) respectively. We will learn the sin, cos, tan formulas for these trigonometric ratios and easy ways to memorize it.
Trigonometry definition: Branch of Mathematics which deals with the measurement of Sides and angles of a triangle and the problems based on them.
Trigonometric Ratios
The ratios of the sides of the sides of a right triangle with respect to its acute angles.
Let us take a right triangle APM as shown in Figure. Here, ∠PAM (or, in brief, angle A) is an acute angle. Note the position of the side PM with respect to angle A. It faces ∠ A. We call it the side opposite to angle A. AP is the hypotenuse of the right triangle and the side AM is a part of ∠ A. So, we call it the side adjacent to angle A.
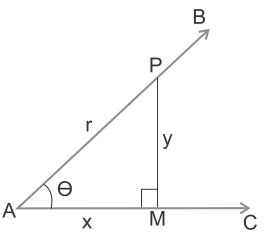
∠ A = θ, AP = r (Hypotenuse) and PM = y (Perpendicular), AM = x (Base), ∠ PMA = 90o
Angle: A figure generated by rotating a given ray along of its end point.
Measurement of an Angle: Amount of rotation of the ray from initial position to the terminal position.
Hypotenuse Definition: the longest side of a right-angled triangle, opposite the right angle.
Perpendicular: at an angle of 90° to a given line, plane, or surface or to the ground.
Base: Side on which right angle triangle stands is known as its base
The Trigonometry Ratios of the angle θ in the triangle APM are defined as follows.
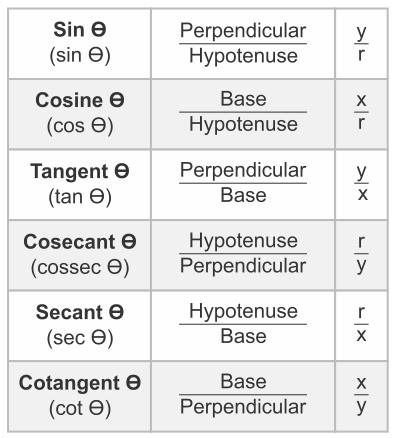
Opposite over Hypotenuse – Sin, Adjacent Over Hypotenuse – Cos, Opposite over Adjacent – Tan, Hypotenuse over Opposite – Cosec, Hypotenuse Over Adjacent – Sec and Adjacent over Opposite – Cotangent,
The ratios defined above are abbreviated as sin θ, cos θ, tan θ, cosec θ, sec θ and cot θ respectively. Note that the ratios cosec θ, sec θ and cot θ are respectively, the reciprocals of the ratios sin θ, cos θ and tan θ. So, the trigonometric ratios of an acute angle in a right triangle express the relationship between the angle and the length of its sides.
Opposite of Sin: Cosecant
Opposite of Cos: Secant
Opposite of Tan: Cotangent
Opposite of Cosecant: Sin
Opposite of Cotangent: Tan
Opposite of Secant: Cosecant
Trig Mnemonics – Some People Have, Curly Black Hair Through Proper Brushing.
Here, Some People Have is for
- Sin θ= Perpendicular/ Hypotenuse.
Curly Black Hair is for
- Cos θ= Base/ Hypotenuse.
Through Proper Brushing is for
- Tan θ= Perpendicular/Base
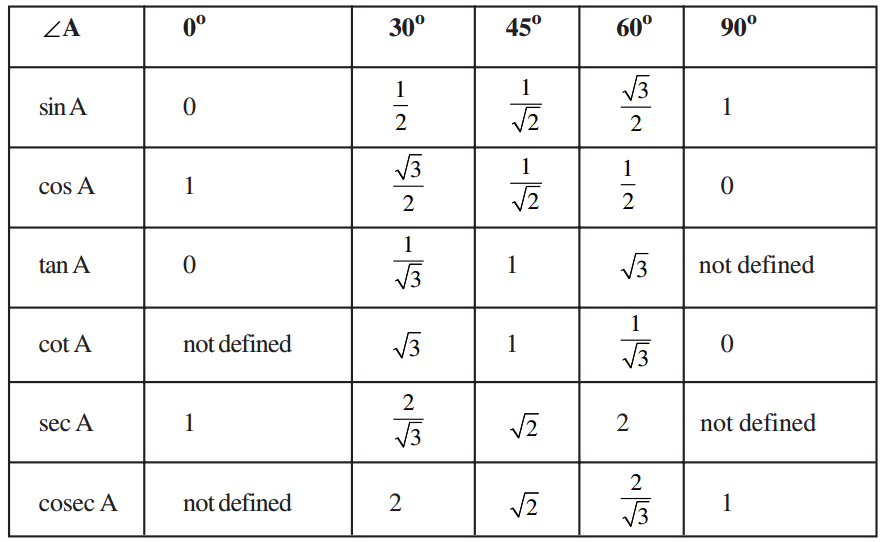
Trigonometric Ratios of Some Specific Angles
We already know about isosceles right angle triangle and right angle triangle with angles 30º, 60º and 90º.
Can we find sin 30º or tan 60º or cos 45º etc. with the help of these triangles?
Does sin 0º or cos 0º exist?
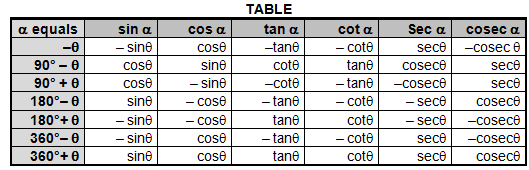
Trig Ratios of Complementary Angles
We know complementary angles are pair of angles whose sum is 90° Like 40°and 50°; 60°and 30°; 20°and 70°; 15° and 75° ; etc.
- sin (90° – θ) = cos θ
- cot (90° – θ) = tanθ
- cos (90° – θ) = sin θ
- sec (90° – θ) = cosec θ
- tan (90° – θ) = cot θ
- cosec (90° – θ) = sec θ

Origin of Trigonometric Ratios
The first use of the idea of ‘sine’ in the way we use it today was in the work Aryabhatiyam by Aryabhata, in A.D. 500. Aryabhata used the word ardha-jya for the half-chord, which was shortened to jya or jiva in due course. When the Aryabhatiyam was translated into Arabic, the word jiva was retained as it is. The word jiva was translated into sinus, which means curve, when the Arabic version was translated into Latin. Soon the word sinus, also used as sine,
became common in mathematical texts throughout Europe. An English Professor of astronomy Edmund Gunter (1581–1626), first used the abbreviated notation ‘sin’.
The origin of the terms ‘cosine’ and ‘tangent’ was much later. The cosine function arose from the need to compute the sine of the complementary angle. Aryabhatta called it kotijya. The name cosinus originated with Edmund Gunter. In 1674, the English Mathematician Sir Jonas Moore first used the abbreviated notation ‘cos’.
Sin Cos Tan are the main functions used in Trigonometry and are based on a Right-Angled Triangle.
Solved Examples on Trig Ratios:
Example-1. If tan A = 3/4 , then find the other trigonometric ratio of angle A.
Solution :
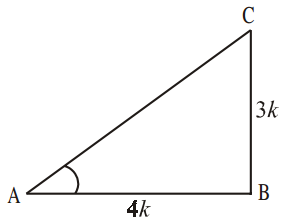
Given tan A = 3/4
Hence tan A = Opposite side/Adjacent side = 3/4
Therefore, opposite side : adjacent side = 3:4
For angle A, opposite side = BC = 3k
Adjacent side = AB = 4k (where k is any positive number)
Now, we have in triangle ABC (by Pythagoras theorem)
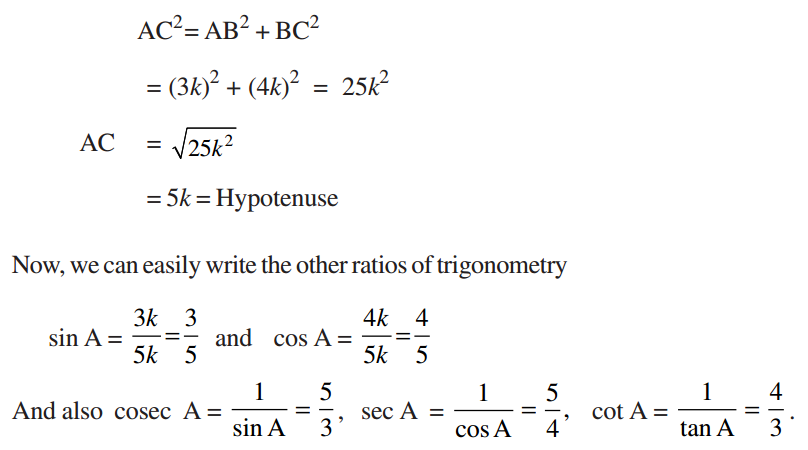
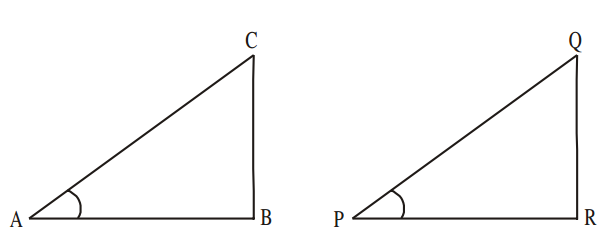
Example 2: If ∠ A and ∠ P are acute angles such that sin A = sin P then prove that ∠ A = ∠ P
Solution : Given sin A = sin P
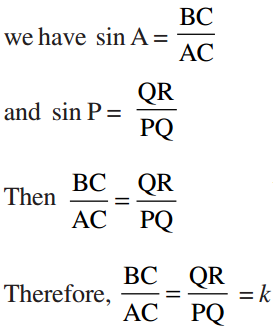

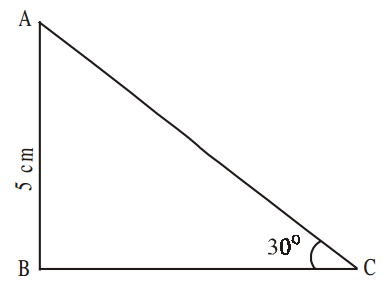
Example 3: In ∆ABC, right angle is at B, AB = 5 cm and ∠ACB = 30o. Determine the lengths of the sides BC and AC.
Solution: Given AB=5 cm and
∠ACB=30o.
To find the length of side BC, we will choose the trignometric ratio involving BC and the given side AB. Since BC is the side adjacent to angle C and AB is the side opposite to angle C.
Therefore,
AB/BC = tan C

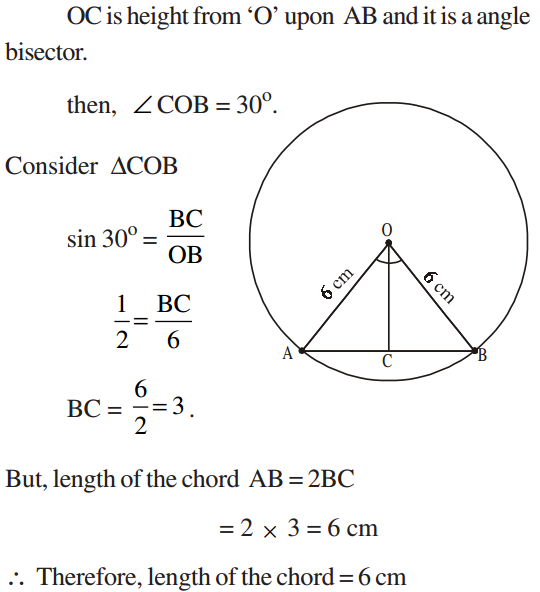
Example 4: A chord of a circle of radius 6cm is making an angle 60o at the centre. Find the length of the chord.
Solution: Given the radius of the circle OA = OB = 6cm
∠ AOB = 60o
Example-5. In ∆PQR, right angle is at Q, PQ = 3 cm and PR = 6 cm. Determine ∠QPR and ∠PRQ.
Solution : Given PQ = 3 cm and PR = 6 cm
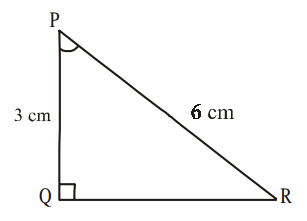

Note : If one of the sides and any other part (either an acute angle or any side) of a right angle triangle is known, the remaining sides and angles of the triangle can be determined.
You can easily remember all trigonometry formulas using super magical hexagon, great way to remember all formulas easily.