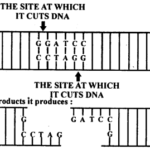
NCERT Solutions For Class 12 Biology Biotechnology: Principles And Processes Topics and Subtopics in NCERT Solutions for Class 12 Biology Chapter 11 Biotechnology: Principles And Processes: Section Name Topic Name 11 Biotechnology:Principles And Processes 11.1 Principles of Biotechnology 11.2 Tools of Recombinant DNA Technology 11.3 Processes … [Read more...]
Important Questions for CBSE Class 12 Biology Adolescence and Drug/Alcohol Abuse
Human Health and Disease Important Questions for CBSE Class 12 Biology Adolescence and Drug/Alcohol Abuse 1.Drugs and alcohol when taken for the purpose other than medicinal or taken in amount or frequencies that disturbs the physical, physiological or psychological functions, is called drug abuse and alcohol abuse, respectively. 2.Statistics show that use of drugs and … [Read more...]
Important Questions for CBSE Class 12 Biology Health, Common Diseases in Human and Immunity
Human Health and Disease Important Questions for CBSE Class 12 Biology Health, Common Diseases in Human and Immunity 1.Health is defined as a state of complete physical, mental and social well-being. (i)The factors which affect human health are: (a)Genetic disorders (b) Infections (c) Lifestyle. (ii)Balanced diet, personal hygiene and regular exercise are very … [Read more...]
Important Questions for CBSE Class 12 Biology Pollution, Solid and Radioactive Wastes
Environmental Issues Important Questions for CBSE Class 12 Biology Pollution, Solid and Radioactive Wastes 1.Pollution is an undesirable change'in the physical, chemical and biological characteristics of air, water, land and soil. Pollutants are agents that cause undesirable change in the environment. The Government of India has passed the Environment Protection Act, … [Read more...]
Important Questions for CBSE Class 12 Biology Nutrient Cycling and Ecosystem Services
Ecosystem Important Questions for CBSE Class 12 Biology Nutrient Cycling and Ecosystem Services 1.The movement of nutrient elements through the various components of an ecosystem is called nutrient cycling or biogeochemical cycles. (i)The amount of nutrients, i.e. carbon, nitrogen, phosphorus, calcium, etc., present in the soil at any given time, is called standing rate. It … [Read more...]